На рисунке показаны две инерциальные системы отсчёта

и

. Они связаны преобразованием Лоренца (лоренцевским гиперболическим поворотом на угол

). Вначале при

два наблюдателя A и B находятся в состоянии покоя относительно системы отсчёта

. Их часы синхронизированы и показывают время

. Решив перейти в другую систему отсчёта, в момент времени

они начинают движение, выдерживая постоянное ускорение

. Ускорившись до скорости

, они отключают двигатели и продолжают двигаться по инерции с достигнутой скоростью

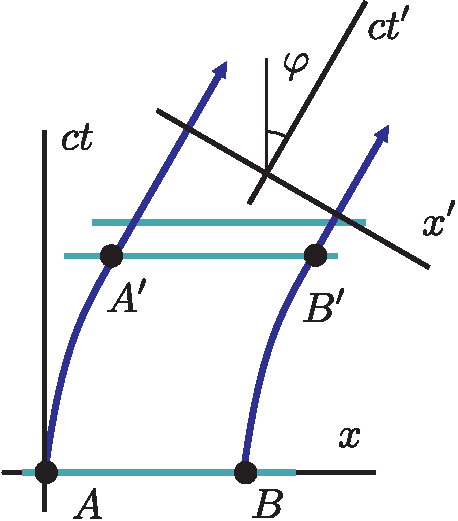
. Ускоренному движению соответствуют участки AA' и BB' на их мировых линиях.
Одновременность двух событий X и Y в системе отсчёта

определяется условием

. Одновременность двух событий X и Y в системе отсчёта

определяется условием

). Мировые линии наблюдателей A и B совпадают по форме и отличаются друг от друга лишь сдвигом в направлении оси x-ов системы отсчёта

. Поэтому собственное время, отсчитанное по бортовым часам наблюдателя A в точке A' совпадает с собственным временем наблюдателя B в точке B', то есть

. Линии одновременности по собственным бортовым часам наблюдателей A и B изображены голубым цветом на рисунке. Даже после перехода на участок движения с постоянной скоростью

эти линии остаются параллельными оси x-ов системы отсчёта

. Таким образом, условие одновременности

по собственным бортовым часам наблюдателей всегда совпадает с условием

, но не совпадают с условием

.
В связи со сказанным естественным является вопрос — какой смысл говорить об относительности одновременности, если при физическом переходе из одной инерциальной системы отсчёта в другую фактической перестройки условия одновременности для физических наблюдателей не происходит?



