Тема сообщения: комплексное пространство, в отличие от вещественного, может задаваться по-разному, бесконечным числом способов, соответственно тому, что каждый вектор пространства лежит в бесконечном множестве плоскостей.
1.
В вещественном линейном пространстве умножение вектора на (вещественное) число можно определить как растяжение (сжатие) вектора.
В комплексном линейном пространстве умножение вектора на (комплексное) число можно определить как растяжение (сжатие) вектора плюс поворот.
Здесь возникает вопрос: в какой плоскости должен производиться этот поворот? Ведь в

-осном пространстве при числе осей больше двух любой вектор лежит в бесконечном множестве плоскостей.
(Для трехосного пространства это хорошо известно, что же касается пространства с большим числом осей, то в нем любой вектор находится по крайней мере в одном трехосном подпространстве, в котором он лежит в в бесконечном множестве плоскостей по свойствам трехосного пространства.)
(Употребляю выражение "

-осное пространство" во избежание недоразумений, которые могут возникать при употреблении выражения "

-мерное пространство", которое идет от числа базисных векторов: при одном и том же числе осей число базисных векторов комплексного пространства вдвое меньше числа базисных векторов вещественного пространства (число измерений пространства равно числу базисных векторов).
(Число осей комплексного пространства четно.)
(Число базисных векторов вещественного пространства равно числу осей.)
(Под плоскостью я понимаю двухосное пространство, это может быть либо двухмерное вещественное либо одномерное комплексное пространство.)
2.
Я думаю, можно сделать так: в

осном пространстве

произвольно выбрать

линейно независимых в вещественном смысле векторов

и для каждого из них произвольно (произвольно -- при

) определить плоскость

умножения на комплексные числа так, чтобы среди этих плоскостей не было совпадающих (о том, что среди них не может быть никаких двух, пересекающихся в прямой, см. ниже, в п. 4). Тем самым определятся плоскости умножения для всех векторов пространства.
В самом деле, пусть разложение вектора

по базису

в плоскостях

равно

где

комплексные числа, тогда при умножении

на комплексное число

имеем

(

умножается на

в плоскости

). При этом вектор

вместе с вектором

определяют плоскость умножения

для вектора

. Разумеется, что плоскость

является плоскостью умножения также и для вектора

.
(Здесь у меня проблема: надо доказать, что при умножении вектора

на другое комплексное число
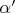
полученный вектор

также лежит в плоскости

, но я не знаю, как это сделать.)
Таким образом, определено умножение векторов на комплексные числа в пространстве

Однако при

его можно определить по-другому.
Вместо плоскостей

возьмем плоскости

при

(достаточно, чтобы хотя бы одно

не было равно

). Тогда, например, при умножении вектора

на то же самое комплексное число

получим (в общем случае?) не вектор

, а некоторый другой вектор

3.
То есть, в отличие от умножения векторов на вещественные числа, которое может быть определено единственным образом (поскольку в любом пространстве, кроме нулевого, каждый вектор лежит в единственной прямой), умножение векторов на комплексные числа -- в пространстве осности не менее четырех -- может быть определено по-разному, бесконечным числом способов, соответственно тому, что каждый вектор пространства лежит в бесконечном множестве плоскостей.
Другими словами, комплексное пространство, в отличие от вещественного, может задаваться по-разному, бесконечным числом способов.
4.
В дополнение попытаюсь доказать два предложения.
Предложение 1.
Любые две плоскости умножения векторов на комплексные числа либо совпадают, либо пересекаются только в нулевой точке.Доказательство. Пусть плоскости

и

являются плоскостями умножения - каждая для лежащих в ней векторов, - и пусть они пересекаются в прямой

, в которой лежит вектор

.
Пусть плоскость

будет плоскостью умножения вектора

, тогда

не может быть плоскостью умножения вектора

, так как вектор может иметь только одну плоскость умножения.
Вместе с тем

является плоскостью умножения вектора

, поскольку плоскость умножения является таковой для каждого из лежащих в ней векторов.
Налицо противоречие, поэтому делаем вывод, что

и

не могут пересекаться в прямой.
В плоскости они также не могут пересекаться, потому что

.
При этом любые две плоскости как подпространства пространства

пересекаются в нулевой точке, отсюда заключаем, что

и

пересекаются только в нулевой точке.
Поскольку плоскости

были выбраны произвольно, можно утверждать, что любые две плоскости умножения векторов на комплексные числа пересекаются только в нулевой точке, ч.т.д..
Предложение 2.
Из всех плоскостей, пересекающихся в одной и той же прямой, только одна является плоскостью умножения векторов на комплексные числа.Доказательство. Пусть плоскости

и

пересекаются в прямой

, в которой лежит вектор

, и пусть плоскость

будет плоскостью умножения вектора

.
Пусть также вектор

лежит в плоскости

и плоскость

является плоскостью умножения вектора

.
Тогда плоскость

является также плоскостью умножения вектора

(поскольку она является плоскостью умножения для всех лежащих в ней векторов), а это невозможно, так как вектор может иметь только одну плоскость умножения.
5.
Относительно четырехмерного случая в одной из статей, ссылку на которую я, к сожалению не могу привести, так как она перестала работать, можно прочитать:
Цитата:
Естественно и в четырёхмерном пространстве называть координатными плоскостями множество точек, у которых какие-либо две из четырёх координат принимают любые числовые значения, а остальные две равны нулю. Например, множество точек вида

мы будем называть координатной плоскостью

четырёхмерного пространства. Сколько же всего таких плоскостей?
Выпишем их:
плоскость

- множество точек, вида

,
плоскость

- множество точек, вида

,
плоскость

- множество точек, вида

,
плоскость

- множество точек, вида

,
плоскость

- множество точек, вида

,
плоскость

- множество точек, вида

.
Из этих шести плоскостей имеется три пары плоскостей, которые пересекаются только в нулевой точке. Это пары

,

и

.
Остальные пары плоскостей пересекаются в прямых.
6.

-осное пространство является прямой суммой

плоскостей, которые пересекаются в одной только нулевой точке.
7.
Кстати, если употреблять термин "

-осное пространство", можно избегать указания на то, является оно вещественным или комплексным.
[Это актуально, разумеется, для четных

так как при нечетных

пространство может быть только вещественным
(если, конечно, не применять конструкцию, которую можно было бы назвать "вещественно-комплексным пространством", где, например, имеется

базисных векторов, которые умножаются на комплексные координаты, и еще один базисный вектор, который умножается на вещественные координаты).]



