23-й конкурс в рамках Математического марафонаКакой-то единой тематикой задачи 23-го конкурса не объединены. Однако, легко разбить конкурсные задачи на три группы. Две из них посвящены традиционно любимым ведущим
арифметике и
комбинаторной геометрии. Третью можно условно озаглавить
"Сон абитуриента в ночь перед ЕГЭ". Окажется ли этот сон кошмарным, узнаем осенью.
Выполняя взятые на себя обязательства, я постарался сделать задачи не слишком трудными. Впрочем, это замечание не касается последней задачи (оценка трудности которой - сама по себе трудная задача).
Еще одна цель, которую я преследовал, составляя задачи - избавиться от чрезмерного перекоса в сторону компьютерщины. Впрочем, от самого компьютера участникам избавляться не стоит, кое-где он пригодится.
Более ранний, по сравнению с предыдущими, старт конкурса не окажет существенного влияния на его дальнейший календарь. Как обычно, активная фаза конкурса начнется осенью. Это не значит, что нельзя решать задачи и присылать решения уже сейчас.
Те, кому это необходимо, могут освежить в памяти (или узнать)
ПРАВИЛА МАРАФОНА.
===========ММ221===============ММ221 (4 балла)
Сколько решений в натуральных числах имеет уравнение

?
===========ММ222===============ММ222 (5 баллов)
На доске написано 10 попарно различных натуральных чисел. После того как 5 из этих чисел разделили на 5, а другие 5 умножили на 5 возникли 10 попарно различных натуральных чисел, отличных от исходных. При этом сумма новых чисел оказалась в 3 раза больше суммы исходных.
Пусть

– наименьшее возможное значение наибольшего из исходных чисел, для которых возможна описанная ситуация.
Сколько существует различных наборов исходных чисел с наибольшим числом

?
===========ММ223===============ММ223 (6 баллов)
Рассмотрим две задачки.
1. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
2. Вася получил за четверть 5 оценок по географии. Ему удалось незаметно исправить в журнале первую попавшуюся из них с тройки на пятерку. Выставляя итоговую оценку, учительница находит среднюю оценку и округляет ее до целой. Какова вероятность, что Васина оценка за четверть повысится при условии, что учительница не выявит подлога, а все допустимые упорядоченные наборы оценок равновероятны?
Какое из условий выгоднее для жуликоватого Васи?
Примечание: Был ли журнал электронным – не важно. Но важно, что колы не ставим: разрешается использовать только оценки 2, 3, 4, 5
===========ММ224===============ММ224 (6 баллов)
В задаче, которую задали на дом Пете и Васе, требовалось найти площади треугольников, на которые разбивается исходный треугольник ABC трисектрисами, проведенными из вершины C. При сверке ответов у Пети и Васи совпали значения двух площадей: 2 и 4. Третья площадь у Пети оказалась равной 10, а у Васи — 20. Найти угол С, если известно, что один из учеников получил за домашнее задание пятерку.
===========ММ225=============== ММ225 (6 баллов)
Найти все значения параметра

, при которых уравнение

имеет два целых корня.
===========ММ226===============ММ226 (5 баллов)
Назовем натуральное число

счастливым, если оно является точной седьмой степенью, а седьмой (при упорядочении по возрастанию) натуральный делитель

равен количеству натуральных делителей

.
А есть ли, вообще, счастье в жизни? В смысле, существуют ли счастливые числа?
===========ММ227=============== ММ227 (7 баллов)
Пусть

- каноническое разложение

. Обозначим через

число

.
Назовем натуральное число

слабым, если уравнение

неразрешимо в натуральных числах, и сильным в противном случае.
Доказать, что сильных чисел бесконечно много.
Найти наименьшее слабое число.
Доказать, что слабых чисел бесконечно много.
===========Терминология ММ228-230===============Несколько (не менее трех) прямых на плоскости называются
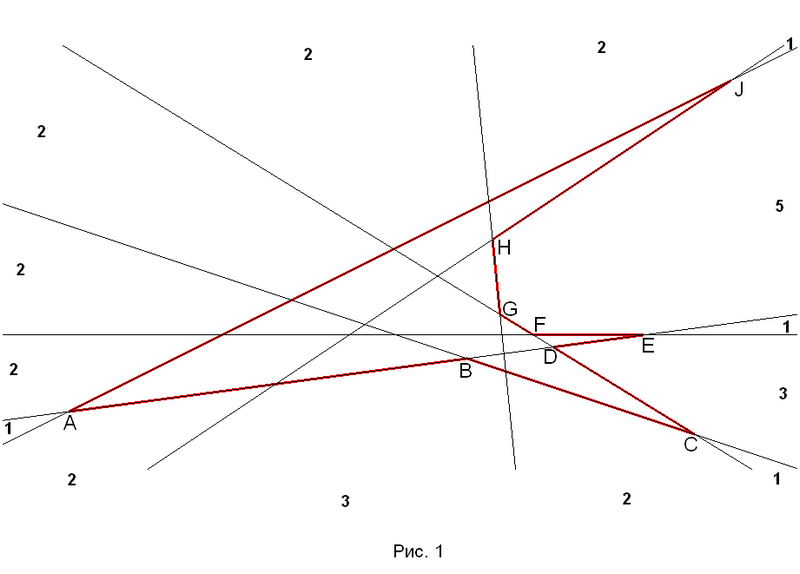
прямыми общего положения, если любые 3 их них высекают треугольник. На рисунке 1 представлены 7 прямых общего положения.
 Внешним контуром
Внешним контуром конфигурации n прямых общего положения назовем многоугольник, высекаемый данными прямыми. На рисунке 1 это красный девятиугольник ABCDEFGHJ.
Внешним циклом конфигурации назовем список количеств вершин внешних областей конфигурации, перечисленных в порядке обхода этих областей (направление и начало обхода не важны). Внешний цикл конфигурации, представленной на рисунке 1:

.
Выпуклыми вершинами внешнего контура назовем вершины, в которых углы меньше развернутого. На рисунке 1 выпуклыми вершинами являются A, C, E, J.
Обратными вершинами назовем вершины внешнего контура, углы при которых больше развернутого. На рисунке 1 это вершины B, D, F, G, H.
Элементарными отрезками назовем отрезки, концы которых являются соседним точками пересечения одной из прямых конфигурации с другими прямыми. Отрезок CD на рисунке 1 элементарен, а отрезок BC – нет.
Элементарными многоугольниками назовем многоугольники, стороны которых являются элементарными отрезками (одна сторона – один отрезок). Например, треугольник DEF на рисунке 1 элементарен, а треугольник BCD – нет.
Впадиной назовем участок внешнего контура между двумя соседними выпуклыми вершинами, содержащий хотя бы одну обратную вершину. Конфигурация, изображенная на рисунке 1 имеет 3 впадины ABC, CDE и EFGHJ.
Вектором граней конфигурации назовем упорядоченный набор из

чисел (где

– количество прямых), первое из которых равно количеству элементарных треугольников, второе – количеству элементарных четырехугольников и т. д. Вектор граней конфигурации, представленной на рисунке 1 –
![$[6, 8, 1, 0, 0]$ $[6, 8, 1, 0, 0]$](https://dxdy-01.korotkov.co.uk/f/8/a/f/8af285b2a1834fa4203130869b1c56a382.png)
.
===========ММ228===============ММ228 (4 балла)
От двух до пяти.
Какое наименьшее число элементарных четырехугольников может быть в конфигурации из семи прямых общего положения?
===========ММ229===============ММ229 (7 баллов)
Петя нарисовал на доске несколько прямых общего положения так, что все попарные точки пересечения прямых попали на чертеж. Вася выписал себе в тетрадь внешний цикл возникшей конфигурации: (1, 4, 3, 1, 4, 1, 2, 2, 3, 2, 3, 1, 2, 3, 1, 2, 4, 2, 1, 3). После этого Петя стер рисунок. Сможет ли Вася восстановить:
1) количество прямых;
2) количество элементарных многоугольников:
3) количество выпуклых вершин;
4) количество элементарных отрезков, ограничивающих внешний контур;
5) количество сторон выпуклой оболочки внешнего контура;
6) суммарное число сторон элементарных многоугольников;
7) количество обратных вершин;
8) количество впадин;
9) количество сторон внешнего контура?
Примечание: Вася – умный.
===========ММ230===============ММ230 (15 баллов)
Может ли вектор граней конфигурации нескольких прямых общего положения начинаться с чисел 157, 5250, 52?
==========================Посмотреть решения задач XXIII конкурса можно
здесь