Кроме того, в физике нет прибора, показывающего квантовое "состояние".
Есть, конечно же. Повторное измерение в том же базисе даёт повторение результата измерения с вероятностью 1 (минус шум, который можно делать сколь угодно малым).. Это означает, что после первого измерения в разложении состояния квантовой системы по измерительному базису остаётся только одно ненулевое слагаемое.
Нет, конечно же. Надо внимательно следить за терминами, чтобы не вводить в заблуждение себя и других. Нет такого чуда - "повторное измерение в том же базисе". Есть опыт с определёнными начальными условиями, и есть описание опыта в КМ-теории вектором состояния в определённом базисе. Выше я чётко определил термин "вектор состояния" (включая и термин "базисный вектор состояния") - это набор амплитуд вероятности

срабатываний детекторов при их сортировке по определённому признаку
при одних и тех же начальных условиях. Все акты имерения ведутся при одних и тех же начальных условиях, тем самым и накапливается статистика отсчётов детекторов, относящаяся к состоянию

А чтобы во всех актах имерения срабатывал один и тот же детектор, надо взять новые начальные условия - специальным образом настроить источник: он должен обеспечить одно из базисных состояний. Например, в роли такого источника можно взять один из выходов упоминавшегося фильтра. Это - просто другая настройка опыта, она изначально не описывается суперпозицией.
"Коллапс" суммы членов суперпозиции к одному слагаемому после первого же акта измерения - нелепая выдумка людей, не желающих понять смысл коэффициентов суперпозиции именно как
амплитуд вероятности.
Такие люди думают, будто эта сумма описывает некую реальную вещь, некий экземпляр, который каким-то чудесным образом "коллапсирует" в акте измерения. Странные это люди; они даже не обращают внимания на то, что:
. в мат. аппарате КМ вообще нет таких уравнений динамики, из которых следовал бы подобный "коллапс";
. без амплитудно-вероятностного смысла суперпозиция становится непригодной для расчётов средних значений, вероятностей - и тем самым такая якобы "квантовая механика" становится вообще непригодной в огромном множестве физических приложений (ФТТ, физика и техника полупроводников и электронных приборов, квантовая химия, и т.п.), где статистическое описание необходимо и где стандартная КМ (амплитудно-вероятностная) успешно служит основой.
. все реально выполненные эксперименты (какие бы завлекательные слова про "коллапс" и т.п. ни писали их авторы во введениях своих статей) спроектированы на основе расчётов статистики по стандартной КМ, и результаты их обрабатываются тоже в соответствии со статистической КМ. Из одиночного акта измерения никто не делает выводов.
. Странные люди даже не обращают внимание на совершенно бредовые "парадоксы", которые у них косяком начинают лезть из их "реалистической интерпретации" вектора состояния - начинается вылезание мистической "роли сознания", швыряние вселенными, троллинг народа одновременно мёртвым и живым котом. Ладно бы этим бредом хоть что-то бы объяснялось, так ведь - нет! "Реалистическая интерпретация" всё равно ничего не говорит о происхождении квантовых эффектов.
Нафига такое дикое фричество, когда во множестве областей физики уже прекрасно себя проявила стандартная статистическая КМ - совершенно не понимаю. (Вернее, понимаю только так: публикабельность статей на такие легковесные квази-КМ темы поддерживают люди, зарабатывающие себе на этом баллы по количеству публикаций; серьёзную-то теор. работу гораздо труднее сотворить, в итоге: "на безрыбье и рак рыба".)
Вот тут я немного не понял: существуют схемы экспериментов, где вероятности событий теоретически ровно 100% и проводить серию для уточнения вероятностей не нужно (только что прочитал про именно такую теорему ГХЦ (GHZ) 1989г, в 2000г проверена экспериментально). Разумеется в практике ровно 100% не получается и статистику приходится всё же накапливать, но Вы же про теорию. Как тут быть, кто кого в каком месте не понял?
(уточняющий ответ)
Предполагаю, Вы не поняли, что у меня речь шла о том, как в КМ-теории определяется
в общем случае понятие "состояние системы". Повторю: "состояние системы" в КМ-теории всегда определяется как совокупность амплитуд вероятности

для полного набора альтернативных событий, возможных при одних и тех же
доступных контролю начальных условиях. Это означает, что:
а)
в общем случае КМ-теория не может предсказать результат одиночного испытания; от испытания к испытанию реализуются разные события (с условными номерами

и теория предсказывает только их вероятности

В свою очередь это означает, что проверка предсказаний теории, а также практическое применение этих предсказаний в разных областях экспериментальной физики и инженерного дела (например, в физике элементарных частиц, в атомной физике, в квантовой химии, в физике твёрдого тела, в том числе в физике и технике полупроводниковых приборов и в материаловедении, в метрологии) всегда основывается на статистическом подходе; а не на однократной реализации какого-либо события.
б) Амплитуды вероятности (а с ними и сами вероятности) зависят от контролируемых условий. Т.е. можно изменять условия, и в теории соответственно будут изменяться комплексные числа

Например, может получиться

так что вероятность события 1 будет

а вероятности остальных событий будут маленькими. Можно ещё немного изменить параметры опыта и получить

так что вероятность события 1 будет

а вероятности остальных событий станут совсем маленькими. И так далее. Наконец, в пределе можно и такой сделать источник, что получится ровно

вероятность события 1 будет

а вероятности остальных событий обратятся точно в ноль. Такую настройку опыта называют базисным состоянием с номером

и обозначают как

или короче

(И тут приходите Вы и говорите: "если вероятность события теоретически ровно 100%, то проводить серию испытаний не нужно; как тут быть, кто кого в каком месте не понял?". Отвечаю: в таком частном случае можно и не проводить, но если провести-таки серию испытаний, то никакого противоречия с общим определением опыта и состояния не возникнет. Поэтому нет смысла в определениях делать исключения для частных случаев, которые хоть и могут быть сформулированы по-другому, но подпадают-таки и под общее определение.
Другими словами: возможность ситуаций, где вероятность события = 100%, не отменяет необходимости накапливать статистику в большинстве прочих ситуаций, в которых вероятности событий получаются разные. Логично поэтому придерживаться единого определения для всего множества ситуаций, где это удаётся.)
(Насчёт же опыта GHZ Вы что-то напутали. Там демонстрируется неклассическая специфика статистики событий без возни с неравенствами Белла, т.е. без утомительного количественного анализа корреляторов, а прямо на качественном уровне; но тоже с утомляющим занятием - с разбором комбинаторных вариантов. Это можно обсудить, но только после достаточно детального изучения учебного материала по мат. аппарату КМ; а иначе будет потрачено много времени и слов, но в итоге всё равно кто-то кого-то где-то не поймёт :).
в) Говорилось об измерении какой-либо наблюдаемой физической величины

Поскольку в физике важны не одна, а многие физические величины (энергия, импульс, момент импульса), то подразумевается возможность перейти к другой постановке опыта - к измерению другой физ. величины, скажем

при прежних начальных условиях. (Просто, не мог же я в один пост впихнуть изложение всей КМ; приходится каждый раз ограничиваться. Теперь вот ещё немножко продолжу. Будет видно, что в состоянии

характеризующемся вероятностью 100% иметь

величина

в общем случае флуктуирует - отличны от нуля амплитуды вероятности разных значений

Этo ещё один аргумент за то, чтобы всем состояниям давать статистическое определение).
Ещё немного о формулах КМ. Пусть на ансамбле таких же квантовых объектов при прежних начальных условиях измеряется не
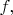
а другая физическая величина, - некая

принимающая тоже

дискретных значений:

Т.е. заменён фильтр: новый фильтр сортирует экземпляры квантового объекта по признаку

Чтобы отличать описание этого опыта от предыдущего, пишем вместо индекса

нумерующий индекс

Амплитуды вероятности срабатывания детекторов на выходах фильтра обозначим, например, как

И базисные векторы состояний в этом опыте будем нумеровать индексом

обозначаем их как

По определению,

есть состояние, в котором событие с номером

из данного набора является достоверным (его амплитуда вероятности равна единице), а остальные события из этого набора не реализуются – их амплитуды вероятности равны нулю в состоянии


Другими словами,

есть состояние с определённым значением

Суперпозиционное состояние ансамбля по отношению к этому опыту (т.е. список амплитуд вероятности

можно записать, по аналогии с прежней записью, в виде

или в эквивалентном виде

где скалярное произведение

есть амплитуда вероятности события

для ансамбля систем в состоянии

Продвинемся в этих рассуждениях ещё на шажок. Если брать в роли

по очереди каждое из прежних базисных состояний

то для них разложение по

-базису будет иметь вид

(где, конечно,

есть амплитуда вероятности события

для ансамбля систем в состоянии

т.е. в состоянии с определённым значением

Подставив такое разложение

в формулу разложения произвольного

по

-базису, получим разложение

по

-базису в виде

Таким образом, амплитуды вероятности в состоянии

по отношению к двум разным наборам событий (т.е. компоненты

и

одного и того же вектора состояния

по отношению к двум разным базисам) связаны соотношением

Следующий шаг (домашнее задание :) в таком построении формализма КМ - получение обратного соотношения, выражающего

через
