В выражении

в скобках стоит семь букв, но сколько элементов они означают? Как я теперь понимаю, тоже семь. Правда некоторые из них могут быть равны друг другу.
А раньше (то есть еще сегодня утром) я думал, что при
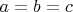
в скобках стоит семь букв, но при этом они означают только пять элементов.
Нет, наверное, утром я понимал правильно. Запись

не означает, что множество

обязательно состоит из семи элементов, их может быть и меньше.
Меня сбило с толку собственное открытие:
Если бы мы могли помещать в фигурных скобках не знаки (например, буквы), которые обозначают объекты, а сами объекты!
К сожалению, это невозможно, но есть объекты, по обозначениям которых мы можем видеть, что это за объекты, то есть какой объект скрывается за данным обозначением.
Если поместить цифры

в соответствующих упорядоченных сочетаниях в фигурные скобки вместе с сопутствующими знаками, такими как

и

, то, как бы ни было выражено некоторое число: например, как

, или как

, или как

, при любом выражении мы видим (или можем вычислить) какое это число.
Таким образом, с точки зрения опознавания, числа представляют собой идеальные объекты, имея их обозначения в фигурных скобках, мы как бы имеем там их самих.
Из этого я сделал ложный вывод, что, когда мы видим в фигурных скобках обозначения чисел, то, сколько этих обозначений, столько и чисел.
Но это не так (как я теперь понимаю). Так же, как и другие объекты, одно и то же число может иметь несколько обозначений.
Сейчас я не имею в виду, что одно и то же число может обозначаться и "

", и "

", и "

", я имею в виду случай

, когда одно и то же число имеет только одно имя, но имеет его три раза. Так что за этими тремя единицами скрывается всего одно число.
Пока я это писал, пришло следующее сообщение, которое подтверждает то, что я сейчас говорю:
Если у нас есть произвольная семерка

, то имеем мы семь объектов или нет?
Если нет, то семерка чего?
Семёрка имён, которые могут относиться к семи
различным объектам, а могут и нет.
То есть отображение из множества имен в множество объектов необязательно инъективно, оно может быть и сюръективно.
Так что я отрекаюсь от того, что написал несколько часов назад:
И запись

обозначает совокупность семи объектов, из которых некоторые могут повторяться, например,

, то есть

это множество с повторяющимися элементами, иначе говоря, мультимножество.
Хотя нет гарантии, что через несколько часов не отрекусь от того, что написал сейчас: я не считаю, что при поиске истины нельзя изменять своему слову.