Множества и объекты

[tolstopuz]

Vladimir Pliassov в сообщении #1520991 писал(а):

Ваша правда! А как написать, что $F$ инъективно?

$\forall i,j\in \{1,2,3,4,5,6,7\}, i\ne j \Rightarrow F_i\ne F_j$

[Vladimir Pliassov]

Эх, Вы меня опередили на несколько секунд, вот что я хотел послать:

$$X=\{a,b,c,d,e,f,g\}, \; \forall i,j\in \{1,2,3,4,5,6,7\}, i\ne j \Rightarrow F_i\ne F_j?$$

и тут пришло Ваше сообщение.

Правда, тут надо еще что-то дописать, наверное:

$$\{1,2,3,4,5,6,7\}\overset{F}{\to } X=\{a,b,c,d,e,f,g\}, \; \forall i,j\in \{1,2,3,4,5,6,7\}, i\ne j \Rightarrow F_i\ne F_j?$$

[kotenok gav]

А теперь надо сказать, что это утверждение должно выполняться либо для всех таких $F$, либо ни для одного.

[tolstopuz]

Vladimir Pliassov в сообщении #1520993 писал(а):

$$\{1,2,3,4,5,6,7\}\overset{F}{\to } X=\{a,b,c,d,e,f,g\}, \; \forall i,j\in \{1,2,3,4,5,6,7\}, i\ne j \Rightarrow F_i\ne F_j?$$

Давайте не упихивать все в одну строку и не использовать неопределенных букв. Выберите какую-нибудь одну букву, смысл которой можно объяснить без упоминания других, и напишите про нее. Потом возьмите следующую и так далее.

[kotenok gav]

(Переписанное утверждение, если что-то будет непонятно)

Пусть $Y=\{1, 2, 3, 4, 5, 6, 7\}$. Тогда утверждение $\exists F\colon Y\to X:\;\forall i,j\in Y\;i\ne j\to F(i)\ne F(j)$ эквивалентно утверждению $|X|=7$.

[xagiwo]

kotenok gav в сообщении #1521019 писал(а):

$\forall F\colon Y\to X\;\forall i,j\in Y\;i\ne j\to F(i)\ne F(j)$

Это утверждение не верно ни при каком $X$, всегда можно взять за $F$ функцию-константу.

[kotenok gav]

Да, действительно, не подумал. Исправил.

[Vladimir Pliassov]

tolstopuz в сообщении #1521017 писал(а):

Vladimir Pliassov в сообщении #1520993 писал(а):

$$\{1,2,3,4,5,6,7\}\overset{F}{\to } X=\{a,b,c,d,e,f,g\}, \; \forall i,j\in \{1,2,3,4,5,6,7\}, i\ne j \Rightarrow F_i\ne F_j?$$

Давайте не упихивать все в одну строку и не использовать неопределенных букв. Выберите какую-нибудь одну букву, смысл которой можно объяснить без упоминания других, и напишите про нее. Потом возьмите следующую и так далее.

1.

Вы имеете в виду одну из букв $a,b,c,d,e,f,g$, например, $a$? Тогда единственное, что я могу о ней сказать, это: $a\in X$, -- и то же самое о других: $a,b,c,d,e,f,g\in X$, -- но это ведь то же самое, что $X=\{a,b,c,d,e,f,g\}$?

2.

По-моему, kotenok gav хорошо написал:

kotenok gav в сообщении #1521019 писал(а):

(Переписанное утверждение, если что-то будет непонятно)

Пусть $Y=\{1, 2, 3, 4, 5, 6, 7\}$. Тогда утверждение $\exists F\colon Y\to X:\;\forall i,j\in Y\;i\ne j\to F(i)\ne F(j)$ эквивалентно утверждению $|X|=7$.

Только надо добавить: $X=\{a,b,c,d,e,f,g\}$.

-- 03.06.2021, 13:36 --

kotenok gav в сообщении #1521009 писал(а):

А теперь надо сказать, что это утверждение должно выполняться либо для всех таких $F$, либо ни для одного.

А как это сделать?

[tolstopuz]

Vladimir Pliassov в сообщении #1521032 писал(а):

Вы имеете в виду одну из букв $a,b,c,d,e,f,g$, например, $a$? Тогда единственное, что я могу о ней сказать, это: $a\in X$, -- и то же самое о других: $a,b,c,d,e,f,g\in X$, -- но это ведь то же самое, что $X=\{a,b,c,d,e,f,g\}$?

То есть вы находитесь в порочном круге и можете определить $a$ и $X$ только друг через друга. Это плохо.

Давайте опять начнем сначала и на этот раз попробуем описать производимые действия словами.

1. Берем произвольную семерку $a,b,c,d,e,f,g$.
2. Составляем из них множество $X$.
3. Теперь возвращаемся к исходной семерке и накладываем на нее условия на неповторяемость элементов.

Вы согласны с этим планом? Если да, попробуем формализовать его.

[Vladimir Pliassov]

Я, конечно, согласен, но у меня возникли некоторые вопросы относительно того, как понимать, что такое эта семерка, так что я на них задерживаюсь.

[tolstopuz]

Давайте задержимся на первом элементе семерки и поймем, что такое $a$. У вас есть с этим проблемы?

[Vladimir Pliassov]

Я сейчас об этом думаю, и это может занять некоторое время, но постараюсь думать побыстрее.

[Vladimir Pliassov]

1.

Если бы мы могли помещать в фигурных скобках не знаки (например, буквы), которые обозначают объекты, а сами объекты!

К сожалению, это невозможно, но есть объекты, по обозначениям которых мы можем видеть, что это за объекты, то есть какой объект скрывается за данным обозначением.

Если поместить цифры $0,1,2,3,4,5,6,7,8,9$ в соответствующих упорядоченных сочетаниях в фигурные скобки вместе с сопутствующими знаками, такими как $+$ и $-$, то, как бы ни было выражено некоторое число: например, как $5$, или как $2+3$, или как $-8+13$, при любом выражении мы видим (или можем вычислить) какое это число.

Таким образом, с точки зрения опознавания, числа представляют собой идеальные объекты, имея их обозначения в фигурных скобках, мы как бы имеем там их самих.

Это не то, что когда в фигурных скобках стоят буквы, и мы не знаем, какой объект скрывается за какой буквой.

В случае с числами мы это знаем (конечно, если допустить называние обозначения чисел буквами).

2.

Давайте разделять понятия множества и записи множества (хотя здесь я, разумеется, призываю Вас делать то, что Вы и так делаете).

В выражении $X=\{a,b,c,d,e,f,g\}$ в скобках стоит семь букв, но сколько элементов они означают? Как я теперь понимаю, тоже семь. Правда некоторые из них могут быть равны друг другу.

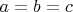
А раньше (то есть еще сегодня утром) я думал, что при $a=b=c$ в скобках стоит семь букв, но при этом они означают только пять элементов.

Пусть при $a=b=c=1, \; d=4,e=5, f=6, g=7$ (то есть элементами множества $X$ пусть будут натуральные числа, которые мы можем без проблем опознавать).

Я предлагаю, чтобы было правило, что запись $\{a,b,c,d,e,f,g\}$ может заменяться на запись $\{1,1,1,4,5,6,7\}$, но не на запись $\{1,4,5,6,7\}$, то есть записи могут заменяться друг на друга, только если они содержат одинаковое число элементов.

Чтобы отличить равенство записей множеств от равенства самих множеств, давайте для равенства записей употреблять знак тождества $\equiv $ и называть это равенство тождеством, а для равенства множеств -- знак равенства $=$.

Тогда $\{a,b,c,d,e,f,g\}=\{1,1,1,4,5,6,7\}=\{1,4,5,6,7\}$ и $\{a,b,c,d,e,f,g\}\equiv \{1,1,1,4,5,6,7\}$, но

$\{1,1,1,4,5,6,7\}\not \equiv \{1,4,5,6,7\}$ и $\{a,b,c,d,e,f,g\}\not \equiv \{1,4,5,6,7\}$.

Нетождественные записи могут быть записями равных множеств.

3.

Так вот, как я теперь понимаю, если у нас есть произвольная семерка $a,b,c,d,e,f,g$, то у нас есть семь объектов, из которых некоторые могут быть равны друг другу, то есть представлять собой один и тот же объект, взятый несколько раз.

И запись $\{a,b,c,d,e,f,g\}$ обозначает совокупность семи объектов, из которых некоторые могут повторяться, например, $\{a,b,c,d,e,f,g\}=\{1,1,1,4,5,6,7\}$, то есть $\{1,1,1,4,5,6,7\}$ это множество с повторяющимися элементами, иначе говоря, мультимножество.

Цитата:

Мультимножество - это множество с повторяющимися элементами https://sci.house/diskretnaya-matematik ... 87700.html

Цитата:

Мультимножество -- модификация понятия множества, допускающая включение одного и того же элемента в совокупность по нескольку раз. (Википедия)

Так что в теории множеств все-таки имеются мультимножества, правда, они заменяются множествами, в которых из их элементов остаются только неповторяющиеся.

Но они в теории множеств есть, так как в ней есть выражение $\{1,1,1,4,5,6,7\}=\{1,4,5,6,7\}$, которое включает в себя $\{1,1,1,4,5,6,7\}$.

Другое дело, что мультимножество и множество это не одно и то же. Как я уже написал в связи с нетождественностью записей:

$$\{1,1,1,4,5,6,7\}\not \equiv \{1,4,5,6,7\}$$

(то есть последнее выражение можно применять не только к нетождественности записей, но и к нетождественности мультимножества и множества.) (Здесь $\{1,1,1,4,5,6,7\}$ -- мультимножество, а $ \{1,4,5,6,7\}$ -- множество.)

При этом $\{1,1,1,4,5,6,7\}= \{1,4,5,6,7\}$.

[Someone]

Vladimir Pliassov в сообщении #1521079 писал(а):

И запись $\{a,b,c,d,e,f,g\}$ обозначает совокупность семи объектов, из которых некоторые могут повторяться, например, $\{a,b,c,d,e,f,g\}=\{1,1,1,4,5,6,7\}$, то есть $\{1,1,1,4,5,6,7\}$ это множество с повторяющимися элементами, иначе говоря, мультимножество.

Вот объясняли-объясняли человеку, и опять двадцать пять.
Как я и подозревал в начале темы, это просто валяние дурака, то есть, троллинг.

[kotenok gav]

Vladimir Pliassov в сообщении #1521032 писал(а):

Только надо добавить: $X=\{a,b,c,d,e,f,g\}$.

Да, надо, иначе получится утверждение $|X|\geq7$.