1.
Для меня это тоже выглядит очень странно. Что это за "самое большое число", которое нужно поставить "после всех натуральных чисел"? Откуда Вы это взяли?
Это здесь:
https://forany.xyz/a-344?pg=12#n19 В ролях элементов "

" и "

" выступает один и тот же объект, который я обозначил

Это просто один и тот же объект, и он выступает в роли самого себя.
Он мог ведь и не быть ни элементом множества

, ни элементом множества

, он был просто прямой, или вектором, или орехом -- безотносительно к этим множествам, -- но так получилось, что ему пришлось стать и тем и другим, то есть выступить сразу в двух ролях: в роли элемента "

" множества

и в роли элемента "

" множества

. Более того, после этого ему пришлось выступить также в роли элемента
множества

, где ему, кстати, можно было бы дать третье имя, например,

, чтобы показать, что он является элементом еще одного множества, тогда было бы

).
Он первичен, а эти множества вторичны: он уже был, когда их еще не было. Я обозначил его

, чтобы не идентифицировать его с этими его тремя ролями, а подчеркнуть его изначальную самостоятельность.
а здесь он выступает в качестве элемента множеств

, где получает имена соответственно "

" и "

" -- то есть те же имена, что и соответствующие элементы
Что за "соответствующие элементы"?
Возьмем множество

. Мы знаем о нем только то, что оно состоит из трех элементов, которые называются

. Теперь наполним представление о нем более конкретным содержанием: пусть

будет монета,

-- кубик,

-- орех. То есть орех выступает в качестве элемента

множества

, где получает имя "

".
Имя элемента не должно зависеть от того, в каком множестве он содержится.
Имя может даваться произвольно, это знак, который может быть чем угодно, лишь бы было договорено, какой объект с ним связывают. Но иногда бывает целесообразно давать имя в зависимости от чего-то, например, элементы множества

часто называют
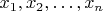
.
какие объекты он имеет в виду -- элементы "

" и "

" множеств

? Это ведь тоже объекты.
Строки "

" и "

" не являются элементами множеств

и

. Эти строки, конечно, являются объектами, но совершенно другой теории (метатеории).
(Почему вы называете

" и "

" строками?)
Ранее Вы написали:
Возможно, Вам будет легче, если Вы поймёте, что "

" и "

" — это не сами объекты, а их имена.
Я не понял, почему вы говорите: "их имена", -- ведь это один объект с двумя именами, -- и стал строить предположения, какие объекты здесь Вы могли иметь в виду: может быть, элементы

" и "

" множеств

-- абстрагируясь от того, что они являются одним и тем же объектом?
2.
Главное, что я понял за эти несколько дней, это то, что множество не имеет повторяющихся элементов.
Вот это слово "повторяющиеся" мне почему-то не приходило, я писал: "одинаковые", "равные", -- но надо было говорить "повторяющиеся элементы" - их нет в множестве.
А также то, что и в объединении совокупности множеств нет повторяющихся элементов, потому что она представляет собой множество.
Пусть нам дана совокупность

множеств

, где

, и при этом

.
Если объединить эту совокупность, то получится множество не из семи, а только из шести элементов, потому что

и

повторяются.
Другими словами, их только шесть, потому что множества

пересекаются в их общем элементе, который в множестве

называется

, а в множестве

--

, то есть в некотором элементе объединения совокупности

.
Число элементов объединения совокупности множеств равно числу всех элементов всех множеств этой совокупности минус число повторений, мы видим это здесь:
