1.
Я понял, что элемент множества не является подмножеством этого множества.
Некоторый объект

может быть элементом некоторого множества

. Вместе с тем он может быть также элементом какого-то другого множества, например, подмножества

множества

.
При этом он не является подмножеством ни множества

, ни множества

.
(То, что объект

сам может быть множеством, здесь несущественно, поскольку он рассматривается как элемент.)
Например,
2. Есть разные подмножества

. Например интервал

или одноэлементное множество

. Элементы подмножества - те же самые точки.
Здесь говорится о множестве

, элементом которого является

, но не говорится, что

есть подмножество

. При этом

есть также элемент множества

.
2.
Вы можете считать, что если

, то

- это не множество, а число, а вот

- множество, состоящее из одного элемента

.
Тогда можно написать:
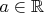
,

, но

,

. И, конечно,

, но

,

.
Элементами

являются некоторые подмножества

(например, объединения интервалов).
Все множество

также является элементом

(третья аксиома). При этом оно не является его подмножеством. Тем не менее, если заключить

в фигурные скобки, можно написать:

-- то есть одноэлементное множество

(элементом которого является объединение всех интервалов) есть подмножество множества

( в частности, потому что

и

пересекаются в элементе

).
3.

и

вообще не пересекаются, потому что элементы

- множества (подмножества

), а элементы

- нет (например, числа).
Если множества пересекаются, то одно из них не может быть элементом другого, верно?
4.
Когда мы говорим о множестве, элементы которого не обязательно сами множества по смыслу*
(например, элементы множества

, то есть числа)
, то вообще нам стоит считать

бессмысленной конструкцией
Но даже если элементы множества

являются множествами "по смыслу", они в отношении множества

все равно рассматриваются не как множества, а как элементы, и поэтому не являются его подмножествами.



