5#: 6 23
7#: 8 89
11#: 14 113
23#: 18 523
29#: 20 887
31#: 34 1327
97#: 36 9551
113#: 44 15683
139#: 52 19609
173#: 72 31397
389#: 86 155921
599#: 96 360653
607#: 112 370261
701#: 114 492113
1153#: 118 1349533
1163#: 132 1357201
1409#: 148 2010733
2153#: 154 4652353
4129#: 180 17051707
4561#: 210 20831323

 из ПСВ по модулю
из ПСВ по модулю 
 , где эти кортежи
, где эти кортежи . Оно конечно при
. Оно конечно при  стремится к 0, но убывает не монотонно.
стремится к 0, но убывает не монотонно. значение данного отношения равно
значение данного отношения равно  , а при
, а при  значение данного отношения равно
значение данного отношения равно  или при
или при  значение данного отношения равно
значение данного отношения равно 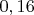 , а при
, а при  значение данного отношения равно
значение данного отношения равно  и.т.д.
и.т.д. значение
значение  и далее при всех
и далее при всех  значение
значение  .
.