Корабль можно поставить всего двумя способами, не четырьмя? Или они сокращаются из-за симметрии?
Я написал "левая верхняя клетка корабля". Корабль от неё можно поставить либо направо, либо вниз.
Тестировал несколько раз по

расположения (по правилам игры, без касаний), ни разу не попалось два совпадающих.
Пусть у нас есть

элементов, которые мы выбираем

раз (с возвращением и независимо) с одинаковой вероятностью

каждый. Вероятность того, что в полученной выборке объёма

найдутся совпадающие элементы, равна

У нас

, и пусть

. Вычислять вероятность совпадений по этой формуле, конечно, весьма накладно, но можно получить приближённую.
Раскрывая скобки, получим

(число слагаемых конечное; 26/III в 21:52 удалил ненужные факториалы, которые тут оказались по недоразумению; далее их и не было)



(знаменатели дробей устроены вполне закономерно, а числители мы заменим соответствующими степенями произведения

, а также продолжим сумму "до бесконечности")

Оценкой погрешности не заморачиваюсь, так как наверняка эта формула (или похожая с

вместо

) уже лет сто как опубликована и с оценкой погрешности. Просто покажу величину погрешности на графиках.
Слева — это графики

и

для

(классическая задача о днях рождения) и для

, а справа — графики разности

.
Вложение:
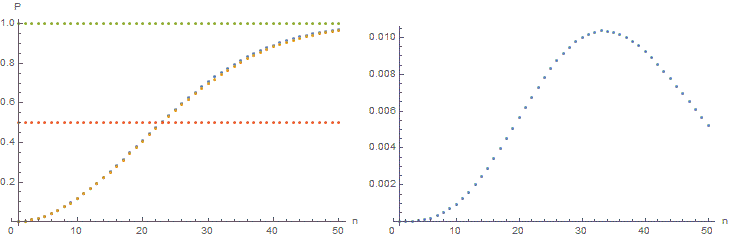 Sovpadenia-365pd.gif [ 5.72 Кб | Просмотров: 1926 ]
Sovpadenia-365pd.gif [ 5.72 Кб | Просмотров: 1926 ]
Вложение:
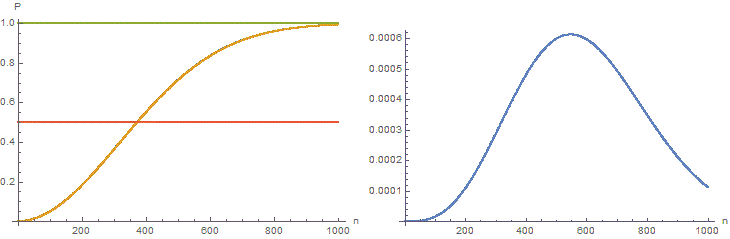 Sovpadenia-100000pd.gif [ 6.41 Кб | Просмотров: 1926 ]
Sovpadenia-100000pd.gif [ 6.41 Кб | Просмотров: 1926 ]
Хорошо видно, что при больших

погрешность маленькая.
Для

и

формула даёт

.
Обратная величина вероятности

, поэтому для получения первого совпадения в среднем требуется

независимых выборок объёмом

. На этом пути можно и оценить объём генеральной совокупности, но для этого требуется сколько-то сотен таких выборок (для

получается

, поэтому таких выборок требуются миллионы).



