Обсуждение книги Верещагина, Шена "Начала теории множеств"

[Sinoid]

пианист в сообщении #1504977 писал(а):

Sinoid
Эта тема тут недавно обсуждалась post1490775.html#p1490775

Как я понял, все крутится вокруг этого:

Verkhovtsev в сообщении #1490771 писал(а):

Каждому проскоченному монотонной функцией интервалу можно сопоставить рац. число, а так как множество рац. чисел счетно, то отсюда следует, что множество разрывов не более чем счетно.

Хм. Пусть $x_n,\,x_{n+1}$ - 2 соседние точки разрыва, $n=0,\,1,\,2,\ldots$ (0 тоже будем натуральным числом). Берем из интервала $\left(x_{n},\, x_{n+1}\right)$, $n=0,\,1,\,2,\ldots$ произвольное рациональное число $r_n$, тогда $r_{n}<r_{n+1}$, потому что любое число из интервала $\left(x_{n},\, x_{n+1}\right)$ меньше любого числа из интервала $\left(x_{n+1},\, x_{n+2}\right)$. Пусть $y=f(x)$ - данная неубывающая функция. Итак, получили: каждой точке разрыва $T_n(x_n,\,f(x_n))$ (здесь уже $n=1,\,2,\ldots$, а не $n=0,\,1,\,2,\ldots$), начиная со второй можно поставить в соответствие интервал $(x_{n-1},\, x_{n})$, правым концом которого является абсцисса этой точки и в каждом из этих интервалов можно выбрать некоторое рац. число $r_{n-1}$, при этом двум различным таким интервалам будут соответствовать и различные рациональные числа, выбранные таким образом. И тогда, т. к. множество различных рациональных чисел$r_0,\,r_1,\,\ldots$, как и любое другое множество рациональных чисел, счетно, то счетно и множество указанных интервалов, а, значит, и множество правых концов этих интервалов подмножество множества разрывов функции $f$ - $\left\{ T_{1},\,T_{2},\ldots\right\}$, но тогда счетно и все множество разрывов функции $f$ - $\left\{T_0,\,T_{1},\,T_{2},\ldots\right\}$, ибо от прибавления к счетному множеству конечного числа элементов его счетность не меняется. Рассуждение ведь верное? И где здесь используется монотонность $f$?

-- 14.02.2021, 00:23 --

И самое плохое в этом рассуждении в том, что его предикативность заложена в него изначально...

[Someone]

Sinoid в сообщении #1504999 писал(а):

Как я понял, все крутится вокруг этого:

Verkhovtsev в сообщении #1490771 писал(а):

Каждому проскоченному монотонной функцией интервалу можно сопоставить рац. число, а так как множество рац. чисел счетно, то отсюда следует, что множество разрывов не более чем счетно.

Хм. Пусть $x_n,\,x_{n+1}$ - 2 соседние точки разрыва,

Вы неправильно поняли, о чём писал Verkhovtsev. Он говорил не о двух точках разрыва, а об одной.

Кроме того, ни откуда не следует, что можно найти хоть одну пару соседних точек разрыва, несмотря на то, что их множество бесконечно.

[Sinoid]

Так. Давайте тогда ясно проговорим, что в теории функций, излагаемой теорией множеств, подразумевается под точкой разрыва? Нет, я, конечно, гуглом сейчас могу найти несколько определений точки разрыва, но я не знаю, каким из них пользоваться в данном случае.

-- 14.02.2021, 01:43 --

Но, явно, не определением из матана.

-- 14.02.2021, 02:04 --

(Оффтоп)

Пока проговорю полностью, что тут:

Null в сообщении #1504746 писал(а):

Попробуйте использовать индексы.
$I_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)$

имеется ввиду точно та же характеристическая функция, о которой я говорил здесь:

Sinoid в сообщении #1504900 писал(а):

На самом деле, несмотря на то, что эта формул верна, применять ее в таком виде не нужно, она в таком виде для решения этой задачи неудобна: для решения этой задачи нужно явное выражение $I_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)$ через $I_{A_{1}}(x),\, I_{A_{2}}(x),\ldots,\, I_{A_{n}}(x)$ (вы обозначали характеристическую функцию через $I\text{ и т. д.}$, а я бы предпочел, чтобы не вызывать путаницы, обозначать ее как в книге, буквой

, определяемая для множества $A$ и элемента $a$ следующим образом: $\chi_{A}(a)=\begin{cases} 0, & \text{если \ensuremath{a\notin A}}\\ 1, & \text{если \ensuremath{a\in A}} \end{cases}$

[Odysseus]

Sinoid в сообщении #1505002 писал(а):

Но, явно, не определением из матана.

Ошибаетесь. Явно определениям из матана.

Sinoid в сообщении #1505002 писал(а):

Давайте тогда ясно проговорим, что в теории функций, излагаемой теорией множеств, подразумевается под точкой разрыва? Нет, я, конечно, гуглом сейчас могу найти несколько определений точки разрыва, но я не знаю, каким из них пользоваться в данном случае.

А какие вы знаете? И причем здесь гугл? Вы же недавно писали:

Sinoid в сообщении #1504745 писал(а):

Я прочитал краткий курс матана Хинчина. Понял там все. Считаю, чисто для топологии этого должно хватить.

[пианист]

Вы по горизонтали смотрите, а надо - по вертикали ;)

Sinoid в сообщении #1504999 писал(а):

Как я понял, все крутится вокруг этого

Не только. Уважаемый Verkhovtsev наглядно объяснил, почему, но в обсуждении выше можно также почерпнуть, как к этому прийти. Ну и дальше тоже интересно.

[Sinoid]

Odysseus в сообщении #1505003 писал(а):

Ошибаетесь. Явно определениям из матана.

Давайте определимся, что же мы будем называть функцией, не являющейся непрерывной. Для это прочитаем определение типичное определение непрерывной функции, взятое из того же краткого курса анализа Хинчина:

и построим предложение, являющееся отрицанием этого определения, пользуясь приемами матлогики (у меня еще после изучения логики такой потребности не возникало, но, как видим, возникла). Для этого расчленим приведенное определение на следующие части:
1. $P$: «функция $f(x)$ называется непрерывной в точке $x_0$»
2. $Q$: «сколь бы мало ни было $\epsilon>0$, существует такое $\delta>0$»
3. $R$: «при любом $h$, по абсолютной величине не превосходящем $\delta$»
4. $S$ $\left|f(a+h)-f(a)\right|<\epsilon$
Тогда приведенное определение формулой можно записать так: $((Q\rightarrow R)\rightarrow S)\rightarrow P$. Правильно?

[Null]

Sinoid в сообщении #1505052 писал(а):

Тогда приведенное определение формулой можно записать так: $((Q\rightarrow R)\rightarrow S)\rightarrow P$. Правильно?

Так писать не стоит. Это не утверждения. Отделять кванторы нельзя.
И $x_0=a$ наверно?

[Sinoid]

Null в сообщении #1505058 писал(а):

Отделять кванторы нельзя.

Не, кванторы позже появятся, когда полезу внутрь $P,\,Q,\,R,\S$, а это придется по-любому. Пока же написал только каркас. А кванторы, кстати, первоначально будут внутри: тот же квантор существования - его что, снаружи писать?

Так что, ход мысли правильный?

[Odysseus]

Sinoid Боюсь, вы все-таки что-то не то и/или не так учили и по матлогике, и по матанализу. Жаль, что вы не прислушались к советам, которые вам недавно давали.

1) Это не "каркас", а нечто совершенно непонятное. Начиная с того, что $Q$ и $R$ это не предикаты, поэтому импликаций к ним применять нельзя. Вы знаете что такое высказывания и, как их обобщение, предикаты? Это же не просто случайным образом вырезанные наборы слов. Мне кажется вам стоит снова разобраться хотя бы с самыми базовыми вещами по матлогике.

2) Аналогично и с матанализом, поскольку впечатление такое будто вы только сейчас узнали про понятие непрерывности функции и пытаетесь в нем разобраться.

3) Без использования кванторов с самого начала - отрицание в данном случае вы никак не построите. Я сейчас посмотрел Хинчина, там кванторы вообще не используются. Он может быть вспомогательным пособием по матанализу, но никак не единственным. Зря, кстати, вы не захотели изучать Зорича (ссылаясь на "слишком много опечаток"), он здесь вам как раз бы помог. Конечно, Зорич это не единственный учебник где они используются, есть и другие. Но, как вам уже рекомендовали, важно правильно подбирать учебники и правильно по ним учиться. Иначе может получиться так, что будете просто зря терять время, но так и не разберетесь не в чем.

Ну и вы опять пытаетесь доказать другим, что все делаете правильно... Зачем тогда про что-то спрашивать?

[Slav-27]

$f$ непрерывна в $a$ $\Longleftrightarrow$ её предел при $x\to a$ существует и равен $f(a)$.

Математическая логика навряд ли поможет, скорее всего только запутает, она не для этого нужна.

[Sinoid]

(Оффтоп)

Прошу прощения за мое исчезновение. Просто нужно было написать длинный ответ и. пока я его писал, мы переехали на съемную квартиру. Но теперь мы 2 месяца точно никуда не будем переезжать.

Odysseus в сообщении #1505078 писал(а):

Начиная с того, что $Q$ и $R$ это не предикаты, поэтому импликаций к ним применять нельзя.

Да, тут вы правы, но

Odysseus в сообщении #1505078 писал(а):

вы все-таки что-то не то и/или не так учили и по матлогике,

тут вы немного погорячились, уверяю вас! Неужели вы думаете, что я на таком серьезном форуме, как этот, позволил бы себе наглость утверждать, что я о чем-то имею представление, не располагая ресурсами это подтвердить? Хотя, возможно, до моего исчезновения с форума вы недостаточно плотно общались со мной и потому знаете меня недостаточно. Хорошо, чтобы подтвердить, что я действительно немного разбираюсь в матлогике, я вижу, что мне нужно продемонстрировать что-то, что я умею в этом разделе математики

(Оффтоп)

Я буду материал брать из изученной мной достаточно неплохо книги "Успенский В. А., Верещагин Н. К., Плиско В. Е. Вводный курс математической логики.". Итак, я хочу показать, как я выводил в исчислении предикатов, имеющим следующие аксиомы (стр. 62):

следующую формулу формальной арифметики: $\forall x(0+x=x)$
Аксиомы формальной арифметики следующие (стр. 77):

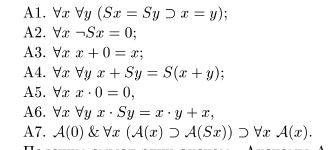
Вывод. Так. Для вывода этой формулы нам потребуется доказать 2 леммы.
Лемма 1. 0+0=0.
Док-во.
1.$\forall x(x+0=x)$ (A3);
2. $\forall x(x+0=x)\supset(0+0=0)$ (а3);
3. $0+0=0$ (МР, п. 1, п. 2)
Лемма 2. $(0+x=x)\supset(0+S(x)=S(x))$
Док-во. В силу теоремы о дедукции достаточно показать, что $(0+x=x)\vdash(0+S(x)=S(x))$. Имеем:
1. $0+x=x$ (гип.)
2. $(0+x=x)\supset(S(0+x)=Sx)$ (а9);
3. $S(0+x)=Sx$ (МР, п. 1, п. 2);
4. $\forall x\forall y(x+Sy=S(x+y))$ (A4);
5. $\forall x\forall y(x+Sy=S(x+y))\supset\forall y(0+Sy=S(0+y))$ (а3)
6. $\forall y(0+Sy=S(0+y))$ (МР, п. 4, п. 5);
7. $\forall y(0+Sy=S(0+y))\supset(0+Sx=S(0+x))$ (а3);
8. $0+Sx=S(0+x)$ (МР, п. 6, п. 7);
9. $(0+Sx=S(0+x))\supset((S(0+x)=Sx)\supset(0+Sx=S(0+x))\wedge(S(0+x)=Sx))$ (а1, в силу тавтологии $A\supset(B\supset A\wedge B)$);
10. $(S(0+x)=Sx)\supset(0+Sx=S(0+x))\wedge(S(0+x)=Sx)$ (МР, п. 8, п. 9);
11. $(0+Sx=S(0+x))\wedge(S(0+x)=Sx)$ (МР, п. 3, п. 10);
12. $(0+Sx=S(0+x))\wedge(S(0+x)=Sx)\supset(0+Sx=Sx)$ (а8);
13. $0+Sx=Sx$ (МР, п. 11, п. 12).
Наконец, все готово для вывода заявленной формулы:
1. $0+0=0$ (лемма 1);
2. $(0+x=x)\supset(0+Sx=Sx)$ (лемма 2);
3. $\forall x((0+x=x)\supset(0+Sx=Sx))$ (Gen, п. 2);
4. $(0+0=0)\supset(_{1}\forall x((0+x=x)\supset(0+Sx=Sx))\supset(0+0=0)\wedge\forall x(_{2}(0+x=x)\supset(0+Sx=Sx))_{2})_{1}$ (а1, в силу тавтологии $A\supset(B\supset A\wedge B)$; здесь цифры внизу означают, что открывающая и закрывающая скобки, стоящие перед одинаковыми скобками, относятся к одной и той же паре открывающей и закрывающей скобок);
5. $\forall x((0+x=x)\supset(0+Sx=Sx))\supset(0+0=0)\wedge\forall x((0+x=x)\supset(0+Sx=Sx))$ (МР, п. 1, п. 4);
6. $(0+0=0)\wedge\forall x((0+x=x)\supset(0+Sx=Sx))$ (МР; п. 3, п. 5);
7. $(0+0=0)\wedge\forall x((0+x=x)\supset(0+Sx=Sx))\supset\forall x(0+x=x)$ (А7);
8. $\forall x(0+x=x)$ (МР, п, 6, п. 7).

Скажите, пожалуйста, по приведенным в оффтопе выкладкам можно сказать, что я хоть что-то понимаю в матлогике? Я еще могу показать решение других задач из той же книги.

Null в сообщении #1505058 писал(а):

Так писать не стоит. Это не утверждения. Отделять кванторы нельзя.

Я прекрасно понимаю, о чем вы говорите: вот я написал высказывательную форму (предикат) $P(x)\rightarrow Q(x)$ (я сейчас рассматриваю случай, когда носитель интерпретации задан). Это еще не высказывание. Высказывание сделает из нее или подстановка вместо $x$ какого-нибудь конкретного значения, принадлежащего носителю интерпретации, или замыкание ее каким-нибудь квантором, например, $\forall$: $\forall x(P(x)\rightarrow Q(x))$. В этом случае формула $P(x)\rightarrow Q(x)$ будет называться областью действия употребленного квантора:

Именно это - предварительно написать область действия квантора (а, возможно, квантороа) - я и пытался сделать тут:

Sinoid в сообщении #1505052 писал(а):

Для этого расчленим приведенное определение на следующие части:
1. $P$: «функция $f(x)$ называется непрерывной в точке $x_0$»
2. $Q$: «сколь бы мало ни было $\epsilon>0$, существует такое $\delta>0$»
3. $R$: «при любом $h$, по абсолютной величине не превосходящем $\delta$»
4. $S$ $\left|f(a+h)-f(a)\right|<\epsilon$
Тогда приведенное определение формулой можно записать так: $((Q\rightarrow R)\rightarrow S)\rightarrow P$. Правильно?

Я еще и переменную(-ые)-то, по которой(-ым) буду замыкать, не знаю, не думал еще над этим. И почему это - предварительное написание области действия квантора - вызвало такую острую реакцию:

Odysseus в сообщении #1505078 писал(а):

Sinoid Боюсь, вы все-таки что-то не то и/или не так учили и по матлогике

я, если честно, плохо понимаю.
Напоследок я аижу, что для того, чтобы не быть голословным, мне не обойтись-таки без того. чтобы указать некоторые из найденных мной опечаток в учебниках. из которых 1 или 2 будет настолько критичными, что использовать тот учебник, в котором она содержится, для изучения соответствующего материала мне представляется не только нецелесообразным, но и вредным.

(Примеры опечаток, недоговоренностей в учебниках)

Итак, после нескольких попыток найти учебник матлогики, который был бы мне под силам, я, следуя советам, полученным на этом форуме, попробовал Игошина. Результатом этой попытки явился, во-первых, огромный список опечаток, обнаруженных в его задачнике, а, во-вторых, когда я на обсуждении очередного запутавшего меня места в его учебнике, сказал, что он, помимо прочего, пишет, что может быть и наподобие такого:

Sinoid в сообщении #1317188 писал(а):

на стр. 67 формулируются 2 теоремы, обратные к данной.

, мне 1 из ЗУ настоятельно начал говорить, чтобы я отказался от идеи использования этой книги для изучения матлогики. Далее, вот пример опечатки в книге Шмидт О. Ю. "Абстрактная теория групп" и она там неединственна, уверяю вас! И это еще далеко не все, что я могу сказать по этому поводу. Просто мне кажется, что мы сильно отклонились от нашей основной темы.

-- 20.02.2021, 23:09 --

Null в сообщении #1504746 писал(а):

Попробуйте использовать индексы.
$I_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)=\frac{1-(-1)^{l_x}}{2}$, где $l_x$ - количество множеств в которые входит $x$.

Очевидно, это связано с тем, что в симметрическую разность данных $n$ множеств входят те и только те элементы их объединения, которые входят в пересечение этих множеств, взятых в любых нечетных количествах. А можно это как-то вывести из определения симметрической разности?

[Null]

Sinoid в сообщении #1505863 писал(а):

А можно это как-то вывести из определения симметрической разности?

Доказать индукцией по количеству множеств?

[Sinoid]

Null в сообщении #1506059 писал(а):

Sinoid в сообщении #1505863 писал(а):

А можно это как-то вывести из определения симметрической разности?

Доказать индукцией по количеству множеств?

Я тоже так думаю. Смотрите. При $n=2$ имеем в силу определения: $A_{1}\triangle A_{2}=(A_{1}\cup A_{2})\backslash(A_{1}\cap A_{2})=(A_{1}\backslash(A_{1}\cap A_{2}))\cup(A_{2}\backslash(A_{1}\cap A_{2}))$ и все очевидно. Теперь рассмотрим случай $n=3$: у меня получилось, что $A_{1}\triangle A_{2}\triangle A_{3}=(A_{1}\backslash(A_{2}\cup A_{3}))\cup(A_{2}\backslash(A_{1}\cup A_{3}))\cup(A_{3}\backslash(A_{1}\cup A_{2}))\cup(A_{1}\cup A_{2}\cup A_{3})$. При необходимости дам подробные выкладки, просто писать долго. Закономерность, как будто, вырисовывается, сейчас раскрываю случай $n=4$: нужно усмотреть общую закономерность.

-- 23.02.2021, 00:42 --

Большое спасибо за участие!

[Sinoid]

Наконец-то я готов подробно расписать случаи $n=3$ и $n=4$. Итак.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
$\fbox{\ensuremath{n=3}}$: $A_{1}\triangle A_{2}\triangle A_{3}=(A_{1}\triangle A_{2})\triangle A_{3}=((A_{1}\triangle A_{2})\backslash A_{3})\cup(A_{3}\backslash(A_{1}\triangle A_{2}))=$ $\begin{matrix}(((A_{1}\backslash A_{2})\cup(A_{2}\backslash A_{1}))\backslash A_{3})\cup\\ (A_{3}\backslash((A_{1}\backslash A_{2})\cup(A_{2}\backslash A_{1})))= \end{matrix}$ $\begin{matrix}[\{(A_{1}\backslash A_{2})\backslash A_{3}\}\cup\{(A_{2}\backslash A_{1})\backslash A_{3}\}]\cup\\{} [\{A_{3}\backslash(A_{1}\backslash A_{2})\}\cap\{A_{3}\backslash(A_{2}\backslash A_{1}\}]= \end{matrix}$

$\begin{matrix}[\{A_{1}\backslash(A_{2}\cup A_{3})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3})\}]\cup\\{} [\{(A_{3}\backslash A_{1})\cup(A_{3}\cap A_{2})\}\cap\{(A_{3}\backslash A_{2})\cup(A_{3}\cap A_{1})\}]=\end{matrix}$

$\begin{matrix}[\{A_{1}\backslash(A_{2}\cup A_{3})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3})\}]\cup\\{} [(A_{3}\backslash(A_{1}\cup A_{2}))\cup(A_{1}\cap A_{2}\cap A_{3})] \end{matrix}$
Получается, я объединяемое множество $A_{1}\cup A_{2}\cup A_{3}$ вот здесь:

Sinoid в сообщении #1506088 писал(а):

у меня получилось, что $A_{1}\triangle A_{2}\triangle A_{3}=(A_{1}\backslash(A_{2}\cup A_{3}))\cup(A_{2}\backslash(A_{1}\cup A_{3}))\cup(A_{3}\backslash(A_{1}\cup A_{2}))\cup(A_{1}\cup A_{2}\cup A_{3})$. При необходимости дам подробные выкладки, просто писать долго.

по рассеянности написал неправильно.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
$\fbox{\ensuremath{n=4}}$ : $A_{1}\triangle A_{2}\triangle A_{3}\triangle A_{4}=(A_{1}\triangle A_{2}\triangle A_{3})\backslash A_{4}\cup A_{4}\backslash(A_{1}\triangle A_{2}\triangle A_{3})=$

$\begin{matrix}[\{A_{1}\backslash(A_{2}\cup A_{3})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2})\}\cup(A_{1}\cap A_{2}\cap A_{3})]\backslash A_{4}\cup\\ A_{4}\backslash[\{A_{1}\backslash(A_{2}\cup A_{3})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2})\}\cup(A_{1}\cap A_{2}\cap A_{3})]= \end{matrix}$

$\begin{matrix}\{A_{1}\backslash(A_{2}\cup A_{3})\}\backslash A_{4}\cup\{A_{2}\backslash(A_{1}\cup A_{3})\}\backslash A_{4}\cup\{A_{3}\backslash(A_{1}\cup A_{2})\}\backslash A_{4}\cup\{(A_{1}\cap A_{2}\cap A_{3})\backslash A_{4}\}\cup\\{} [A_{4}\backslash\{A_{1}\backslash(A_{2}\cup A_{3})\}]{}_{1}\cap[_{2}A_{4}\backslash\{A_{2}\backslash(A_{1}\cup A_{3})\}]_{2}\cap[_{3}A_{4}\backslash\{A_{3}\backslash(A_{1}\cup A_{2})\}]_{3}\cap[_{4}A_{4}\backslash(A_{1}\cap A_{2}\cap A_{3})]_{4}= \end{matrix}$

$\begin{matrix}\{A_{1}\backslash(A_{2}\cup A_{3}\cup A_{4})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3}\cup A_{4})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2}\cup A_{4}\}\cup\{(A_{1}\cap A_{2}\cap A_{3})\backslash A_{4}\}\cup\\ [_{1}(A_{4}\backslash A_{1})\cup\{A_{4}\cap(A_{2}\cup A_{3})\}]{}_{1}\cap[_{2}(A_{4}\backslash A_{2})\cup\{A_{4}\cap(A_{1}\cup A_{3})\}]_{2}\cap[_{3}(A_{4}\backslash A_{3})\cup\{A_{4}\cap(A_{1}\cup A_{2})\}]_{3}\cap\\ [_{4}A_{4}\backslash(A_{1}\cap A_{2}\cap A_{3})]_{4}= \end{matrix}$

$\begin{matrix}\{A_{1}\backslash(A_{2}\cup A_{3}\cup A_{4})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3}\cup A_{4})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2}\cup A_{4}\}\cup\{(A_{1}\cap A_{2}\cap A_{3})\backslash A_{4}\}\cup\\ \Large{\mbox{\ensuremath{[}}\normalsize{\mbox{\ensuremath{[_{1}(A_{4}\backslash A_{1})\cup(A_{4}\cap A_{2})\cup(A_{4}\cap A_{3})]_{1}\cap[_{2}(A_{4}\backslash A_{2})\cup(A_{4}\cap A_{1})\cup(A_{4}\cap A_{3})]_{2}\cap}}}}\\ [_{3}(A_{4}\backslash A_{3})\cup(A_{4}\cap A_{1})\cup(A_{4}\cap A_{2})]_{3}\cap\\ \Large{\mbox{\normalsize{\mbox{\ensuremath{[_{4}A_{4}\backslash(A_{1}\cap A_{2}\cap A_{3})]_{4}}}}}}\mbox{\ensuremath{]\normalsize{\mbox{=}}}} \end{matrix}$

$\begin{matrix}\{A_{1}\backslash(A_{2}\cup A_{3}\cup A_{4})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3}\cup A_{4})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2}\cup A_{4}\}\cup\{(A_{1}\cap A_{2}\cap A_{3})\backslash A_{4}\}\cup\\ \Large{\mbox{\ensuremath{[}\normalsize{\mbox{\ensuremath{\ensuremath{(A_{4}\backslash(A_{1}\cup A_{2})\cup((A_{4}\cap A_{3})\backslash A_{2})\cup(A_{1}\cap A_{2}\cap A_{4})\cup(A_{1}\cap A_{3}\cap A_{4})\cup((A_{3}\cap A_{4})\backslash A_{1})\cup}}}}}}\\ \Large{\mbox{\ensuremath{\normalsize{\mbox{\ensuremath{(A_{2}\cap A_{3}\cap A_{4})\cup(A_{3}\cap A_{4})}}}]}}}\cap[_{3}(A_{4}\backslash A_{3})\cup(A_{4}\cap A_{1})\cup(A_{4}\cap A_{2})]_{3}\cap\ensuremath{[_{4}A_{4}\backslash(A_{1}\cap A_{2}\cap A_{3})]_{4}}\Large{\mbox{\ensuremath{]}}}= \end{matrix}$

$\begin{matrix}\{A_{1}\backslash(A_{2}\cup A_{3}\cup A_{4})\}\cup\{A_{2}\backslash(A_{1}\cup A_{3}\cup A_{4})\}\cup\{A_{3}\backslash(A_{1}\cup A_{2}\cup A_{4}\}\cup\{(A_{1}\cap A_{2}\cap A_{3})\backslash A_{4}\}\cup\\ \Large{\mbox{\ensuremath{[}}}\normalsize{\mbox{\ensuremath{(\underbrace{A_{4}\backslash(A_{1}\cup A_{2}\cup A_{3}))\cup((A_{1}\cap A_{2}\cap A_{4})\backslash A_{3})}_{\cap(A_{4}\backslash A_{3})}\cup}}}\\ \underbrace{((A_{1}\cap A_{4})\backslash(A_{1}\cup A_{2}))\cup((A_{1}\cap A_{3}\cap A_{4})\backslash A_{2})\cup(A_{1}\cap A_{2}\cap A_{4})\cup(A_{1}\cap A_{3}\cap A_{4})}_{\cap(A_{4}\cap A_{1})}\cup\\ \underbrace{(A_{1}\cap A_{2}\cap A_{3}\cap A_{4})\cup(A_{1}\cap A_{3}\cap A_{4})}_{\cap(A_{4}\cap A_{1})}\cup\\ \underbrace{((A_{2}\cap A_{4})\backslash(A_{1}\cup A_{2}))\cup(A_{1}\cap A_{2}\cap A_{4})\cup(A_{1}\cap A_{2}\cap A_{3}\cap A_{4})\cup((A_{2}\cap A_{3}\cap A_{4})\backslash A_{1})}_{\cap(A_{4}\cap A_{2})}\cup\\ \underbrace{(A_{2}\cap A_{3}\cap A_{4})\cup(A_{2}\cap A_{3}\cap A_{4}}_{\cap(A_{4}\cap A_{2})})\Large{\mbox{\ensuremath{]}}}\cap(A_{4}\backslash(A_{1}\cap A_{2}\cap A_{3}))= \end{matrix}$

И что с этим со всем этим дальше делать ума не приложу. Не подскажите?

-- 25.02.2021, 21:59 --

Ну, по опыту предыдущих подобных изысканий я подозреваю, что копаю куда-то не туда: уж слишком все громоздко получается, явный признак.

[Sinoid]

Кажется, я понял, как нужно рассуждать, и, кажется, в этом:

Sinoid в сообщении #1506599 писал(а):

Ну, по опыту предыдущих подобных изысканий я подозреваю, что копаю куда-то не туда: уж слишком все громоздко получается, явный признак.

я был прав. Из определения симметрической разности нужно выводить не вот это утверждение:

Sinoid в сообщении #1505863 писал(а):

Очевидно, это связано с тем, что в симметрическую разность данных $n$ множеств входят те и только те элементы их объединения, которые входят в пересечение этих множеств, взятых в любых нечетных количествах.

и не вот эту вот формулу:

Null в сообщении #1504746 писал(а):

$I_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)=\frac{1-(-1)^{l_x}}{2}$, где $l_x$ - количество множеств в которые входит $x$

, а следующую формулу:

$$\fbox{\ensuremath{\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)=\dfrac{1-(1-2\chi_{A_{1}}(x))(1-2\chi_{A_{2}}(x))\ldots(1-2\chi_{A_{n}}(x))}{2}}}$$

А из нее совершенно естественным образом и последует первое из утверждении, процитированных в этом посте. Для этого вывода будем использовать следующие формулы:
\begin{gather} \chi_{A\cup B}(x)=1-(1-\chi_{A}(x))(1-\chi_{B}(x))\\ \chi_{A\backslash B}(x)=\chi_{A}(x)(1-\chi_{B}(x)) \end{gather}
Кроме того, я буду пользоваться тем очевидным фактом, что, если $a$ и $b$ принимают независимо друг от друга значения, принадлежащие множеству $\left\{ 0,\,1\right\} $, $m$ и $n$ - произвольные отличные от нуля натуральные числа, то $a^{m}b^{n}=ab$. Итак, проверяем базу, рассматриваем случай $n=2$. По определению имеем: $A_{1}\triangle A_{2}=(A_{1}\backslash A_{2})\cup(A_{2}\backslash A_{1})$. Тогда, в силу формул (1), (2) и упомянутого факта будем иметь: $\chi_{A_{1}\triangle A_{2}}(x)=\chi_{(A_{1}\backslash A_{2})\cup(A_{2}\backslash A_{1})}(x)=1-(1-\chi_{A_{1}\backslash A_{2}}(x))(1-\chi_{A_{2}\backslash A_{1}}(x))=$

$1-(1-\chi_{A_{1}}(x)+\chi_{A_{1}}(x)\chi_{A_{2}}(x))(1-\chi_{A_{2}}(x)+\chi_{A_{1}}(x)\chi_{A_{2}}(x))=$

$1-(1-\chi_{A_{1}}(x)+\chi_{A_{1}}(x)\chi_{A_{2}}(x)-\chi_{A_{2}}(x)+\chi_{A_{1}}(x)\chi_{A_{2}}(x)-\chi_{A_{1}}(x)\chi_{A_{2}}^{2}(x)++\chi_{A_{1}}(x)\chi_{A_{2}}(x)-\chi_{A_{1}}^{2}(x)\chi_{A_{2}}(x)+\chi_{A_{1}}^{2}(x)\chi_{A_{2}}^{2}(x))=$

$1-(1-\chi_{A_{1}}(x)-\chi_{A_{2}}(x)+2\chi_{A_{1}}(x)\chi_{A_{2}}(x))=\chi_{A_{1}}(x)+\chi_{A_{2}}(x)-2\chi_{A_{1}}(x)\chi_{A_{2}}(x)=$

$\dfrac{2\chi_{A_{1}}(x)+2\chi_{A_{2}}(x)-4\chi_{A_{1}}(x)\chi_{A_{2}}(x)}{2}=\dfrac{1-(1-2\chi_{A_{1}}(x)-2\chi_{A_{2}}(x)+4\chi_{A_{1}}(x)\chi_{A_{2}}(x))}{2}=$

$\dfrac{1-(1-2\chi_{A_{1}}(x)-2\chi_{A_{2}}(x)(1-2\chi_{A_{1}}(x)))}{2}=\dfrac{1-(1-2\chi_{A_{1}}(x))(1-2\chi_{A_{2}}(x))}{2}$

Итак, база индукции выведена из определения. Далее, как обычно, доказываем формулу для $n+1$, исходя из предположения ее верности для $n$:

$\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}\triangle A_{n+1}}(x)=\chi_{(A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n})\triangle A_{n+1}}(x)=$

$\chi_{((A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n})\backslash A_{n+1})\cup(A_{n+1}\backslash(A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}))}(x)=$

$1-(1-\chi_{(A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n})\backslash A_{n+1}}(x))(1-\chi_{A_{n+1}\backslash(A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n})}(x))=$

$1-(1-\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)+\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x))(1-\chi_{A_{n+1}}(x)+\chi_{A_{n+1}}(x)\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x))=$

$1-(\underbrace{1-\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)+\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)}_{\cdot1}$

$\underbrace{-\chi_{A_{n+1}}(x)+\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)-\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}^{2}(x)}_{\cdot(-\chi_{A_{n+1}}(x))}$

$\underbrace{+\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)-\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}^{2}(x)\chi_{_{A_{n+1}}}(x)+\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}^{2}(x)\chi_{A_{n+1}}^{2}(x)}_{\cdot\chi_{A_{n+1}}(x)\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)})=$

$1-(1-\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)-\chi_{A_{n+1}}(x)+2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x))=$

$\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)+\chi_{A_{n+1}}(x)-2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)=$

$\dfrac{2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)+2\chi_{A_{n+1}}(x)-4\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)}{2}=$

$\dfrac{1-(1-2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)-2\chi_{A_{n+1}}(x)+4\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)\chi_{A_{n+1}}(x)}{2}=$

$\dfrac{1-(1-2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)-2\chi_{A_{n+1}}(x)(1-2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x)))}{2}=$

$\dfrac{1-(1-2\chi_{A_{1}\triangle A_{2}\triangle\ldots\triangle A_{n}}(x))(1-2\chi_{A_{n+1}}(x))}{2}=$

$\dfrac{1-(1-2\chi_{A_{1}}(x))(1-2\chi_{A_{2}}(x))\ldots(1-2\chi_{A_{n}}(x))(1-2\chi_{A_{n+1}}(x))}{2}$.

Скажите, пожалуйста, это верное доказательство? Есть ли какие-нибудь замечания, комментарии? Заранее благодарю.

-- 28.02.2021, 02:13 --

Здесь также использовалась ассоциативность симметрической разности, формулы (1) и (2), а еще упомянутый факт.