Здравствуйте. Возник вопрос с задачей из учебного пособия "Лекции по физике плазмы" (И. А. Котельников, Г. В. Ступаков): Плотность ионов в плазме как функция времени имеет вид ступеньки: она равна

при
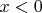
и

при

, причем

. Найти распределение потенциала и плотности электронов, если электронная температура равна

.
Расскажу ход своих мыслей. Записываем 2 уравнения Пуассона: для области
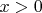
и
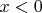
, концентрацию ионов в обеих областях задана, а концентрацию электронов можно получить из распределения Больцмана (или можно попробовать получить концентрацию электронов из условия квазинейтральности). Вот такое у меня получилось уравнение, определяющее потенциал, в общем виде:



(условие квазинейтральности)
Но у меня не получается задать граничные условия, чтобы определить константы. Можно попробовать сшить потенциалы на границе, наложив непрерывность, но этого недостаточно. Я также не до конца уверен в определении концентрации электронов. Если кто-то имел дело с этой задачей или знает как правильно задать граничные условия и определить концентрацию электронов, подскажите пожалуйста.



