Если предположить, что я понял, что именно вы рисуете (но я в этом не уверен) - нет.
Я немного понял, чтобы понять как работает телескоп, возможно лучше будет сначала разобраться с глазом представив его как линзу и экран, что олицетворяет хрусталик и сетчатку.
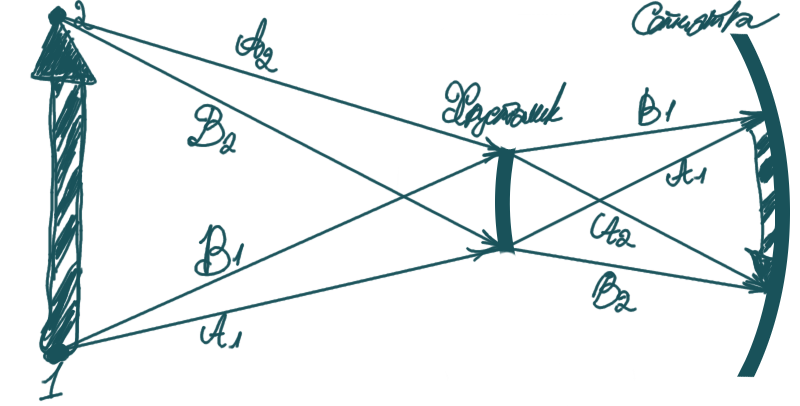
Лучи света

,

,

,

что восходят с точек

и

есть граничные случаи, между ними огромное количество лучей которые несут ту же информацию о соответствующей точке! Теперь мне становиться понятным
суть пересечения в геометрической оптике, — если пересекаются хотя бы два луча несущих одну и ту же информацию, то их пересекается огромное количество, то есть много пересечений если есть хотя одно пересечение и что-то бесконечно малое если нету ни одного пересечения на рисунке. По этой причине формирование изображение происходит путем пересечения разных лучей восходящих от той же самой точки на объекте который складывается с огромного множества точек (никогда бы не подумал что понимания пару страниц теории множеств поможет в геометрической оптике).
Что такое угол под которым видно объект? Это угол между лучами

и

или

и

? — Ответ на этот вопрос (как я понимаю): эти углы равны! Имеет смысл говорить об угле по которым виден объект только тогда когда то с чего этот объект виден (хрусталик глаза) есть нечто маленькое в сравнении с расстоянием до объекта! По сему разница между этими углами ничтожно мала, глаз (будучи не ничтожно малым) наверное берет среднее значение, или как-то так, при этом угловой размер

будет таким что с него можно получить линейный размер некого объекта который приближается таким что есть частью полусферы, в сравнении с окружностью этой полусферы радиусом равным расстоянию до объекта:

примерно таким образом глаз должен вычислять расстояние и размеры.
Что в общем случае приведет к увеличению проницающей способности (возможности видеть более тусклые объекты). Правда, без окуляра (если пытаться смотреть в телескоп глазом) все равно обойтись не удастся.
То есть тут у меня воображения спрашивает вот так: "светосила" есть интенсивность той же информации? Например гор на Луне, оно ведь не несет катастрофически отличной информации? Хотя если строго то наверное ми не можем знать всю информацию об объекте с помощью света который от него идет ибо какая-то часть все ровно не попадет в наш объектив.
Говорить про угловой размер изображения на сетчатке малоосмысленно, речь шла о наблюдаемом угловом размере объекта. Да, максимальный угол между лучами (можно без сравнения с чем-либо).
Я понял! (По идее понял.) Угловой размер на сетчатке будет только если мы посмотрим на пятно на сетчатке чем-то со стороны, и чем оно меньше тем меньше будет его угловой размер для. Просто не мог понять что угловой размер это означает что мы либо воображаем некого точечного наблюдателя (ну как там радиотелескопии), или такой наблюдатель действительно пренебрежим своими размерами с расстоянием до объекта, например когда хрусталик человека имеющий размер там, не знаю, пару десятых сантиметра и расстояние до Луны, когда человек на нее смотрит. Хух... Как-то ступор прошел, начинаю куда-то двигаться в понимании геометрической оптики, кстати книг по ней чтобы понятно но не слишком просто мало. У меня например купа всего по механике, электродинамике, квантовой механики, теории относительности, но особо такого по геометрической оптике нету.
Угол - неопределимое понятие, закладывающееся в раннем детстве. Или не закладывающееся, как повезёт.
Градус угла - есть мера усталости глаза при обозрении угла от угла его до угла.
Угол в народном изустном творчестве:
- Во главу угла ставьте угол!
- Прямой угол кипит при температуре в девяносто градусов.
- Жизнь нельзя увидеть под тем же углом, но можно под тем же градусом.
Я интуитивно всегда знал что такое угол (мож и не правильно), это нечто между двумя напрявлениями в пространстве, которому мы можем приписать любое, удобно нам значение. Но мне нравиться

измерение полной окружности, и таким образом измерение углов, насколько помню это с Вавилонского Царства, у них там еще шестидесятичная система числения была. Градусы полного круга

наверно будут в ней как

(число пальцев) по идее очень удобно было.
Ой, о шестидесятеричной системе это неправильно, мозги одно думают, пальцы иное печатают. Конечное же

в десятичной системе, арабскими цифрами в шестидесятеричной будет

, то есть нолик на "нулевом" положении шестидесятки и шестерка на первом, ибо триста шестьдесят делится на шестьдесят без остатка и получается шесть.
Пользуясь тем что надо редактировать сообщение чтобы вернули из бана тему, еще дополню своими подальшими разбирательствами, теперь я могу объяснить что например значит вот этот рисунок из книги Вайнберга "Пояснюючи світ. Історія сучасної науки".
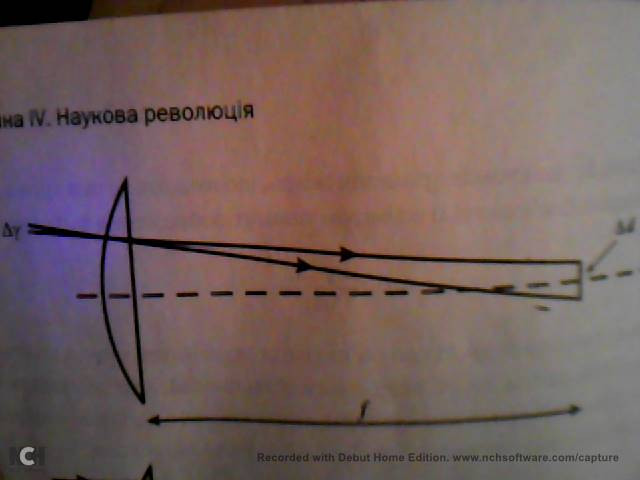
Промежуток углов параллельных лучей

есть не что иное как угол

или угол

на рисунке вашего покорного слуги выше, более того, поскольку размер линзы и расстояние очень сильно разнятся, линза маленькая в сравнении, мы считаем этот угол постоянным на всей плоскости линзы куда падают лучи! Это
в приближении и есть угловой размер объекта, вот здесь была моя основная тупость, я не мог нормально организовать мысли и воображение чтобы это понять... Как в мультике о панде "из-за волнений не видно истины".
Теперь мы вплотную (ну я точней) подошли к понимаю увеличения телескопа простейшей системы. Но сначала пару слов об объектах. Точка имеет угловой размер

хотя лучи к линзе приходят под углом допустим если точечный источник света далеко но не слишком далеко. Почему тогда мы не увидим "размытой точки"? Потому что угол

для точки нулевой, нету второй точки от которой шли бы лучи к линзе, объектив соберет все лучи от точки что в нее попадают в одной точке. Тоже самое будет если все лучи параллельны, то есть только один вид параллельности, и можем поставить линзу так чтобы все эти лучи были параллельны главной фокальной оси. В таком случае угол

тоже будет нулевой и мы не получим никакой информации об объекте кроме того где оно находиться на полусфере, ибо все лучи от него соберутся в одну точку за линзой. Вот так.
Теперь вопрос с которым еще предстоит разобраться: увеличит ли объектив, без окуляра, изображение если за ним поставить экран? Для этого используем рисунок супермодератора, только немного увеличив его.
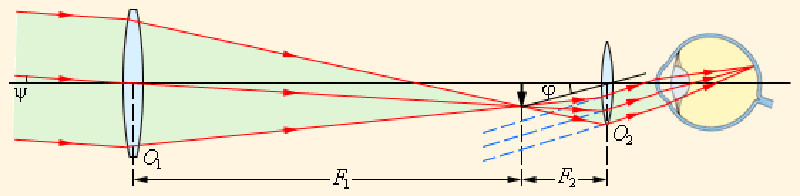
Параллельные лучи под углом

есть такие с диапазона различных углом множеств параллельных лучей, границы этого диапазона например на рисунке профессора Вайнберга это угол

, а на моем это угол

если расстояние до объекта много больше размера линзы объектива. Ну насколько я понял. Более того, на рисунке модератора эти три параллельные входящие лучи есть
все от одной верхушки стрелочки. Вообразить это лично мне довольно трудно, даже если ваш покорный слуга правильно понял.
Теперь почему один объектив без окуляра не увеличит изображение? — Потому-что если поставить экран далеко за фокусом, то лучи от какой либо точки, например верхушки разойдутся, а это не имеет смысла в плане того что каждая точка этого "телесного расхождения, чем дальше от фокуса тем больше будет напоминать "луч — одна точка", то есть луч это что-то бесконечно тоненькое.
Если поставить экран в фокальной плоскости, увеличиться ли размер изображения с видимым размером?
Видимый глазом размер, видимый им потому-что в глазе есть линза, а линза объектива больше, поэтому интенсивность сфокусированного света будет больше. Более того, размер изображения на экрана допустим с тоненькой линзой диаметром один метр, и линзой диаметром один сантиметр, наверное будет разница. Хотя и не особо понятен механизм этого... Вообщем тут надо еще подумать.
П. С. Это уже мне троечка за старания и разбирательства, ну не двойка точно.




