Помогите с принципом работы телескопа Кеплера

[Pphantom]

frostysh в сообщении #1439277 писал(а):

Зачем разбираться сначала с линзами? — Не могу вообразить как оно там после объектива получается

Выше уже написали много правильного, но все же добавлю: детальное разбирательство с тем, что будет происходить со светом в реальной линзе - это большая и сложная отдельная наука, которая для понимания оптики в целом совершенно не нужна. Безусловно, для человека, который собирается конструировать оптические приборы - это хлеб, который должен быть известен как "Отче наш", но за пределами этой узкой области (и некоторых смежных) в эти детали никто не вдается.

Поэтому сначала начните с приближения тонкой линзы с постулированными свойствами. Когда этот этап будет полностью освоен, тогда (если останется желание) можно будет заняться большей детализацией.

[arseniiv]

frostysh в сообщении #1439277 писал(а):

Объект имеет угловой размер, если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!

Да, я кстати выше недостаточно ясно выразился: мы же интересуемся увеличением вообще, в том числе увеличением расстояний (точнее углов) между точечными объектами. Вот про них как раз удобно получить ответ, взяв сначала эти точечные объекты бесконечно удалёнными.

[Dmitriy40]

frostysh в сообщении #1439277 писал(а):

Если расстояние до объекта будет тысячу фокусных, или десять тысяч и при этом угловой размер линзы будет различимый с заданной точностью, то тогда и расстояние $FF'$, те есть разница между расстоянием где надо поставить экран чтобы изображение не размытое было и фокусным, должно быть различимо,

Нет, не должно, оно зависит от фокусного расстояния и от расстояния от объекта до линзы, но не от её диаметра. Посмотрите, все лучи из одной точки объекта пересекаются в одной же точке экрана, независимо на какой высоте от центра линзы они прошли. Значит можно линзу по краям немного обкусить, изображение стрелочки не изменится, лучей ведь очень-очень много и потеря нескольких по краям ничего не значит, оставшиеся соберутся всё равно ровно там же. И ещё обкусить. И ещё. Или наоборот увеличить линзу и новые лучи соберутся всё равно в нужной точке экрана. И ещё увеличить. Ничего не изменится.

[Xey]

frostysh в сообщении #1439277 писал(а):

если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!

Смысл есть.
Хотя для сегодняшних телескопов все звезды являются точечными объектами и видны в виде кружков, определяемых дифракцией и абберациями. Телескоп позволяет увеличить разрешение (видеть по отдельности две близкие звезды), увеличить точность определения углов между звездами и видеть очень слабые звезды.

[Pphantom]

Xey в сообщении #1439350 писал(а):

Хотя для сегодняшних телескопов все звезды являются точечными объектами и видны в виде кружков, определяемых дифракцией и абберациями.

Строго говоря, неверны и первая, и вторая часть утверждения. Не все звезды - точечные, а вид изображений тех, угловые размеры которых не разрешаются (их, конечно, подавляющее большинство), определяется в основном не дифракционным пределом.

[frostysh]

Dmitriy40 в сообщении #1439279 писал(а):

frostysh в сообщении #1439277 писал(а):

Если расстояние до объекта будет тысячу фокусных, или десять тысяч и при этом угловой размер линзы будет различимый с заданной точностью, то тогда и расстояние $FF'$, те есть разница между расстоянием где надо поставить экран чтобы изображение не размытое было и фокусным, должно быть различимо, мне вот интересно как это расстояние зависит от углового размера линзы если смотреть с объекта...

Да, при изменении расстояния до объекта будет меняться расстояние от фокуса до экрана. Но! При удалении объекта в бесконечность это расстояние (от экрана до фокуса) стремится к нулю. И (лень считать) скажем для миллиона фокусных разница расстояний от линзы до фокуса и до экрана станет меньше микрона (ну к примеру, не считал) — а такое мелкое смещение на резкость уже не повлияет, это Вы наверняка уже можете оценить сами (простейшая пропорция как у меня выше). И для вех более далёких объектов, а телескоп предназначен для очень далёких объектов, это расстояние (от фокуса до экрана) будет практически тем же.

Чтобы понять эту пропорцию по идее нужно понимать как идут луче всередине линзы, буду разбераться скоро с этим тоже.

Dmitriy40 в сообщении #1439279 писал(а):

Я там ошибся и зачеркнул, для упрощения можно считать весь объектив одним сплошным куском стекла с кривой передней поверхностью, только на которой и происходит преломление, а дальше лучи идут строго прямо. Продолжив этот кусок стекла до окуляра и выполнив его как заднюю поверхность куска получим монолитный телескоп с двумя преломляющими поверхностями. Удобно для расчётов. Может даже иметь ограниченно практическое применение ...

Вот только такое сплошное упрощение как тогда на нормальный случай, с воздухом между объективом и окуляром переносить, но вообще интересно, я то думал что там посредине обязательно должна быть среда оптически не такая как окуляр и объектив.
А ваше сообщение было процитировано еще до зачеркивания, пока отвечал на ваше, еще написали сообщения, на эти тоже ответил, а потом только запостил.

Dmitriy40 в сообщении #1439279 писал(а):

Это проще. И достаточно первого Вашего рисунка, вот ваш готовый объектив телескопа, уже даже с ходом лучей в нём. Осталось справа приставить правильно окуляр (вторую линзу с более коротким фокусом) и нарисовать ход новых (!) лучей от уже изображения после объектива дальше вправо. А ещё правее нарисовать точку глаза (да, точки вполне достаточно) и провести лучи из неё к финальному изображению после окуляра (оно обычно мнимое!) и к исходному объекту — разница углов к изображению и к объекту и будет увеличением телескопа.

Если честно, что-то все ровно недопойму, ведь то будет увелечительный прибор для чего-то не очень далеко так как лучи от точек объекта идут не параллельно, в смысле от каждой точки по отдельности, а я вот начертил для чего-то очень далекого. Разобрался с угловыми размерами и геометрией параллельных лучей от крайних точек объекта, это для далеких.

В смысле попробуем следуя советам на форуме сначала разобраться с механизмом без влезания в собственно как лучи линзах себя ведут, следуя простым правилам построения изображений, а потом будем разбирать детальней.



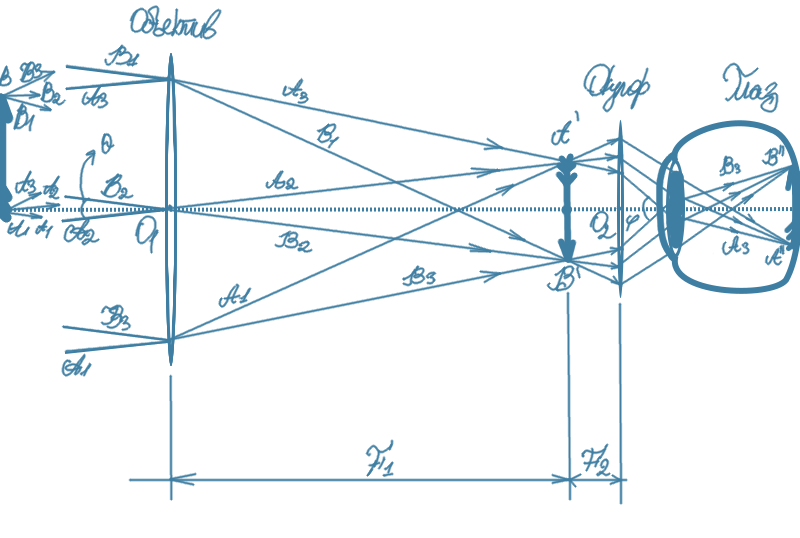
Где $O_{1}$ и $O_{2}$ есть оптические центры, ну и вообще центры, линз объектива и окуляра соответственно, $F_{1}$ и $F_{2}$ — фокусы этих линз. Линейный размер в видимом поперечнике это отрезок $AB$ объекта, например Альфы Центавры какой-то, это могут быть тысячи и тысячи километров. Угловой размер под которым объект виден без телескопа это $\theta$, угловой размер под которым объект виден при использовании телескопа — $\varphi$ соответственно, при увеличении углового размера информация об объекте не теряется ибо там лучей бесконечное множество.
Начертя круг, точней окружность с центром в точке $O_{1}$, радиусом $F_{1}$, мы увидим что длина отрезка воображаемого изображения $A'B, там нету экрана, поэтому и воображаемое, мы увидим, что при достаточной малости угла $\theta$ и длины $A'B'$, эта длина пропорциональна углу

$$A'B' = \dfrac{\theta 2 \pi F_{1}}{360^{\circ}},$$

почему все на фокальной плоскости фокусируется написано выше и разберу точней поздней. Очевидно что отношение углов $\varphi / \theta$ будет увеличение телескопа, но как связать это с параметрами самых линз? В одной книге предлагается способ, который не особо понятен, и рисунок тоже не особо понятен, ибо я вообще не пойму почему если большой объект поместить в фокусе линзы то лучи на выходе будут параллельные. Пояснение примерно следующее: давайте запустим лучи в обратном направлении, типу окуляр стал объективом, тогда для окуляра нарисуем окружность с центром в $O_{2}$, и проделаем тоже, считая по ходу действия $A'B'$ и $\varphi$ очень маленьким, и поэтому воображаемое изображение которое создает телескоп, будет сходное с реальным объектом который посылает лучи во все стороны, хотя на самом деле лучи после фокуса $F_{1}$ будут расходится только внутри некого угла. Так вот запишем для окуляра следующую равность

$$A'B' = \dfrac{\varphi 2 \pi F_{2}}{360^{\circ}},$$

теперь можно увидеть примерную зависимость увеличения от фокусных расстояний объектива и окуляра

$$1 = \dfrac{\varphi F_{2}}{\theta F_{1}},$$

отсюда

$$Zoom = \dfrac{\varphi}{\theta} = \dfrac{F_{1}}{F_{2}}.$$

Вот рисунок с книги к этому всему.

Dmitriy40 в сообщении #1439279 писал(а):

frostysh в сообщении #1439277 писал(а):

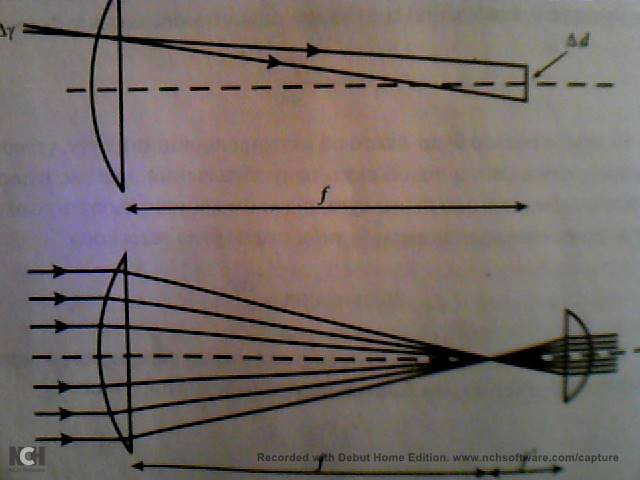
то смысла на него смотреть нету в плане увеличения в этот телескоп!

Да.
Есть правда другие тонкости, где увеличение таки нужно и для точечных объектов, но это уже не геометрическая оптика и пока рано (а может и вообще не нужно).

Вот так смотри, и разберусь с этой геометрической оптикой телескопа, с помощью этого форума и его участников, хоть поспокойней будет на душе в чем-то.

Pphantom в сообщении #1439280 писал(а):

frostysh в сообщении #1439277 писал(а):

Зачем разбираться сначала с линзами? — Не могу вообразить как оно там после объектива получается

Выше уже написали много правильного, но все же добавлю: детальное разбирательство с тем, что будет происходить со светом в реальной линзе - это большая и сложная отдельная наука, которая для понимания оптики в целом совершенно не нужна. Безусловно, для человека, который собирается конструировать оптические приборы - это хлеб, который должен быть известен как "Отче наш", но за пределами этой узкой области (и некоторых смежных) в эти детали никто не вдается.

Поэтому сначала начните с приближения тонкой линзы с постулированными свойствами. Когда этот этап будет полностью освоен, тогда (если останется желание) можно будет заняться большей детализацией.

Вот выше вычертил увеличение, следуя советам, слава богам понял что от каждой точки конкретного далекого объекта лучи идут параллельно, но если взять весь объект, то лучи от него идут не параллельно, а внутри некого угла — называемого угловым размером.

Теперь надо понять:

• разницу между воображаемым изображением, без экрана на фокусной плоскости объектива, и реальным объектом если его туда поместить;
• какая разница при этом будет для окуляра, с фокусной плоскостью там же;
• и почему лучи от объекта в фокусной плоскости идут параллельно после окуляра (это наверное немного надо понять как лучи внутри линзы летят), и должны ли так идти лучи от воображаемого изображения?

arseniiv в сообщении #1439281 писал(а):

frostysh в сообщении #1439277 писал(а):

Объект имеет угловой размер, если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!

Да, я кстати выше недостаточно ясно выразился: мы же интересуемся увеличением вообще, в том числе увеличением расстояний (точнее углов) между точечными объектами. Вот про них как раз удобно получить ответ, взяв сначала эти точечные объекты бесконечно удалёнными.

Да, правильно, всмысле не правильно, а ваш покорный слуга так считает что правильно. Действительно целесообразно брать расстояние бесконечным для точечных объектов с которых там что-то например складывается, в этом смысл телескопа.

arseniiv в сообщении #1439281 писал(а):

frostysh в сообщении #1439277 писал(а):

Объект имеет угловой размер, если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!

Да, я кстати выше недостаточно ясно выразился: мы же интересуемся увеличением вообще, в том числе увеличением расстояний (точнее углов) между точечными объектами. Вот про них как раз удобно получить ответ, взяв сначала эти точечные объекты бесконечно удалёнными.

Я в смысле что если угловой размер линзы будет неразличим если смотреть на линзу с объекта, то от каждой точки объекта до линзы будут идти параллельные лучи от каждой конкретной точки объекта, хотя с разными углами к главной фокальной оси в зависимости от конкретной точки. То есть, если проиллюстрировать.



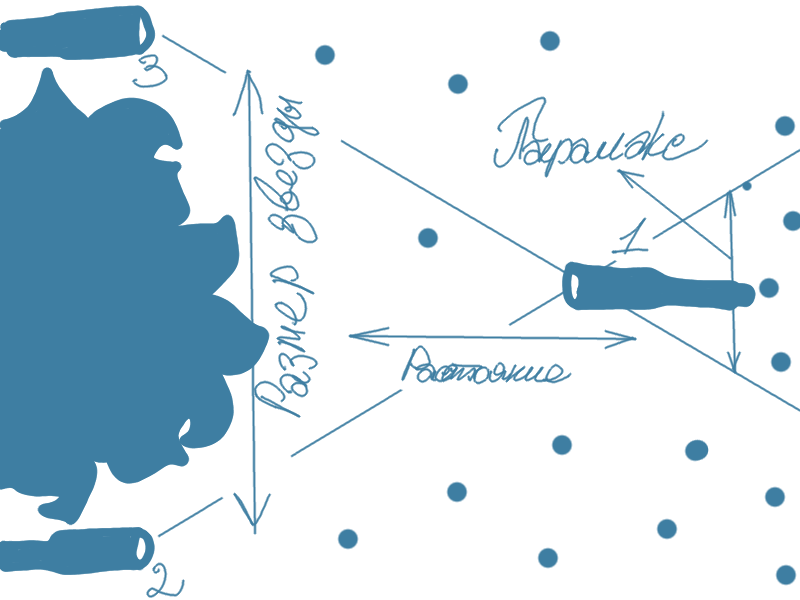
У нас три телескопа: $1$, $2$, $3$, одинаковых. Если в телескопы два и три виден телескоп один не как точка, а как-что с угловым размером, для этого наши телескопы должны быть или супер увеличительные, или размером порядка звезды... Вообще если виден угловой размер первого телескопа, то посмотрев с первого телескопа на зведу, мы получим случай для объектива — линза и объект на очень далеком расстоянии, во много раз большем чем фокус, но все же не бесконечном.
Если же углового размера телескопа один не видно, но виден его паралакс при переходе от второго телескопа к третьему например, то посмотрев с первого на звезду, мы получим для объектива случай — объект на бесконечно далеком расстоянии.
Если же и параллакса не видно с телескопов два и три, тогда посмотрев телескопа один — мы увидим просто светящуюся точку без углового размера. Вот так вот, такая у меня лично модель этого всего.

Xey в сообщении #1439350 писал(а):

frostysh в сообщении #1439277 писал(а):

если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!

Смысл есть.
Хотя для сегодняшних телескопов все звезды являются точечными объектами и видны в виде кружков, определяемых дифракцией и абберациями. Телескоп позволяет увеличить разрешение (видеть по отдельности две близкие звезды), увеличить точность определения углов между звездами и видеть очень слабые звезды.

Де юре две точечные звезды и расстояние между ними, это для угловых размеров тоже самое что и физический объект размером с это расстояние. Дифракции и абберации, это наверно неудобно будет лучами изображать, или есть какие-то модели такие для подобного в геометрической оптике?

[Dmitriy40]

frostysh в сообщении #1439497 писал(а):

мы увидим что длина отрезка воображаемого изображения $A'B, там нету экрана, поэтому и воображаемое,

Нет, оно не воображаемое, там можно поместить экран и оно на нём появится, так что оно действительное. Экран можно сделать и полупрозрачным, тогда он не будет сильно мешать работе окуляра.

frostysh в сообщении #1439497 писал(а):

почему все на фокальной плоскости фокусируется написано выше и разберу точней поздней.

Таково свойство применяемых оптических деталей под названием "линза", фокусировать параллельные лучи на фокальной плоскости, а идущие параллельно оптической оси — в фокусе. Просто линзы именно так и изготавливаются, чтобы вот это и делать. Есть много других оптических деталей, делающих с лучами что-то другое, а вот линзы делают это, фокусируют.

На первом рисунке глаз излишен, достаточно угла $\varphi$, что будет с лучами дальше правее (в глазу) — дело другое и к телескопу мало относящееся.

frostysh в сообщении #1439497 писал(а):

мы увидим, что при достаточной малости угла $\theta$ и длины $A'B'$, эта длина пропорциональна углу

$$A'B' = \dfrac{\theta 2 \pi F_{1}}{360^{\circ}},$$

Это не совсем верно, это будет длина дуги окружности, а не длина хорды/изображения, тут надо куда-то синус угла прикрутить, и тогда можно не ограничиваться малыми углами. Но для телескопа да, углы малы и можно (и нужно для упрощения понимания) и без синуса.

frostysh в сообщении #1439497 писал(а):

В одной книге предлагается способ, который не особо понятен, и рисунок тоже не особо понятен, ибо я вообще не пойму почему если большой объект поместить в фокусе линзы то лучи на выходе будут параллельные.

Это вполне стандартный способ, чтобы не выводить всё снова воспользоваться симметричностью ситуации. В геометрической оптике лучам всё равно идут они слева направо, или справа налево, излучаются далёкой звездой и попадают на экран или излучаются экраном (например монитор LCD) и уходят к звезде. Ничего при этом не меняется. Потому можете брать своё изображение в фокусе и запускать от него лучи куда угодно, например ровно по тем же "дорожкам" что уже нарисованы — и они пойдут ровно по ним и никак иначе.
Если у Вас путаница с понятиями вход и выход, то разверните листок с чертежом на 180° чтобы изображение оказалось слева, а объект справа.

frostysh в сообщении #1439497 писал(а):

будет сходное с реальным объектом который посылает лучи во все стороны, хотя на самом деле лучи после фокуса $F_{1}$ будут расходится только внутри некого угла.

Расходиться они будут конечно во все стороны (если рассматривать не только лучи от далёкого объекта после объектива, они то в ограниченном угле), но те что не попадут в линзу объектива (или окуляра) нам не интересны, они поглотятся трубой телескопа и полезного действия не совершат. Но лучей мно-о-ого и какие-то попадут и в линзы — и они и построят нужное изображение. И даже их очень много (бесконечное количество, как возможных лучей в рамках заданного угла).

frostysh в сообщении #1439497 писал(а):

отсюда

$$Zoom = \dfrac{\varphi}{\theta} = \dfrac{F_{1}}{F_{2}}.$$

Да, это правильная формула, и вывод её вроде достаточно правильный.

frostysh в сообщении #1439497 писал(а):

разницу между воображаемым изображением, без экрана на фокусной плоскости объектива, и реальным объектом если его туда поместить;

Это лучше понимать/разбираться с лупой, одиночной линзой, не с телескопом как (относительно) сложной оптической системой.
Возьмите тонкую собирающую линзу (с одним параметром фокусное расстояние), поместите объект на утроенном фокусном расстоянии, нарисуйте ход лучей. Потом на удвоенном. Потом на полуторном. Потом на 1.1 фокусного (можно и пропустить если уверены в своих силах). Заметьте что изображение всегда действительное, его можно увидеть на экране в данном месте. Потом точно на фокусном. Потом на 0.75 фокусного. В последнем случае должны получить расходящиеся лучи, справа нигде не пересекающиеся, т.е. изображения объекта не создающие. Но! Можно их продолжить влево за линзу, виртуально, пунктиром, и вот там они вполне себе пересекутся. И если бы справа был глаз (совершенно неважно как устроенный), то увидев такие расходящиеся лучи ему бы показалось что они идут от объекта слева где пересекаются их продолжения. Разумеется никакого объекта или изображения там нет, но глазу казалось бы что есть. И потому это кажущееся изображение называют мнимым. Заметьте что оно больше реального объекта, хотя и дальше от линзы. И не перевёрнутое относительно объекта. Если теперь построить угол под которым из некоей далёкой точки справа (дальше к примеру десятикратного фокусного расстояния) виден исходный объект без линзы и мнимое изображение через линзу, то будет видно что через линзу угол больше. Это и есть увеличение лупы.

frostysh в сообщении #1439497 писал(а):

и почему лучи от объекта в фокусной плоскости идут параллельно после окуляра (это наверное немного надо понять как лучи внутри линзы летят), и должны ли так идти лучи от воображаемого изображения?

Не надо ничего внутри линзы понимать. Летят и летят, и пусть летят как хотят. Главное что происходит с ними снаружи линзы. А снаружи Вы уже дважды построили картинку, для объектива. Переверните её так чтобы изображение было слева, а входные лучи справа, переназовите изображение объектом, лучи из него входными, лучи вправо после линзы выходными, а объект где-то справа далеко-далеко изображением — и будет Вам готовое решение почему лучи из фокальной плоскости уходят параллельными. Снова повторю, это просто свойство применяемых финтифлюшек под названием "линза", они специально именно так и сделаны.
Насчёт же воображаемого изображения, лучам после испускания уже без разницы чем или кем они испущены, хоть объектом, хоть звездой, хоть свечкой, хоть изображением чего-то, хоть реальным, хоть воображаемым — главное чтобы они хоть чем-то испустились, а дальше уже просто законы геометрической оптики (как очень маленького и сильно упрощённого кусочка физических законов, никакой магии или чудес тут нет).

frostysh в сообщении #1439497 писал(а):

Вот так вот, такая у меня лично модель этого всего.

Немного туманно и запутанно, но по сути вроде верно.

frostysh в сообщении #1439497 писал(а):

Дифракции и абберации, это наверно неудобно будет лучами изображать, или есть какие-то модели такие для подобного в геометрической оптике?

Не стоит пока в это лезть, рано, запутаетесь.
Коротко скажу, просто чтобы не оставлять в недоумении.
Дифракцию лучами да, неудобно, если вообще возможно, тут существенна волновая картина света, что в геометрической оптике игнорируется.
Аберрации можно и лучами, но неудобно, проще в терминах изображений и фокальных поверхностей (они уже не плоскости) и искажений поля зрения.
Надо понимать что это уже не идеальная геометрическая оптика, это уже следствие или физической природы света, или погрешностей изготовления оптических деталей (линз).

[arseniiv]

Dmitriy40 в сообщении #1439518 писал(а):

Не надо ничего внутри линзы понимать.

Кроме того если начать строить ход лучей внутри линзы, придётся или мириться с тем, что она строго говоря уже не тонкая и ведёт себя хитрее, или придётся пренебрегать тем или сем, чем ТС по-моему заниматься упорно не хочет. Так до понимания дойти очень трудно, к тому же холизм вообще иллюзия, потому что мы не можем рассмотреть всех факторов в настоящих явлениях, и раз чем-то мы пренебрегаем даже просто потому что не знаем, что оно есть, то всё же неразумно не попренебрегать уже и сознательным образом. Но эта идея конечно не так проста и не сразу получает в голове одобрение. У меня когда-то в каких-то масштабах тоже такое было, но может быть потому что меня никто и не направлял, а тут ситуация вроде иная.

[frostysh]

Dmitriy40 в сообщении #1439518 писал(а):

На первом рисунке глаз излишен, достаточно угла $\varphi$, что будет с лучами дальше правее (в глазу) — дело другое и к телескопу мало относящееся.

Это не совсем верно, это будет длина дуги окружности, а не длина хорды/изображения, тут надо куда-то синус угла прикрутить, и тогда можно не ограничиваться малыми углами. Но для телескопа да, углы малы и можно (и нужно для упрощения понимания) и без синуса.

Рисунок я для себя рисовал, с глазом намного легче мне вообразить. Теперь о синусе угла и хорде хотелось бы разобраться в данному случае...





Половина хорды в окружности с радиусом один, построенная на двойном угле который идет с центра этой окружности будет синус этого угла. В нашем случае возьмем $\sin{\dfrac{\theta}{2}}$, но даже зная что любой хорде, допустим $BA$, мы можем начертить круг с центром на любой точке на линии перпендикулярной этой хорде и такой что выходит с центра этой хорды, то есть например в точке $O_{1}$, то как нам узнать радиус этой окружности чтобы потом узнать какую поправку внести у формулы чтобы было точней? Я подумаю над этим... Ну хотя для получения зависимости увеличения телескопа от отношения фокусных расстояний, это не имеет по сути значения, результат одинаков будет, но все же.

Dmitriy40 в сообщении #1439518 писал(а):

Это вполне стандартный способ, чтобы не выводить всё снова воспользоваться симметричностью ситуации. В геометрической оптике лучам всё равно идут они слева направо, или справа налево, излучаются далёкой звездой и попадают на экран или излучаются экраном (например монитор LCD) и уходят к звезде. Ничего при этом не меняется. Потому можете брать своё изображение в фокусе и запускать от него лучи куда угодно, например ровно по тем же "дорожкам" что уже нарисованы — и они пойдут ровно по ним и никак иначе.
Если у Вас путаница с понятиями вход и выход, то разверните листок с чертежом на 180° чтобы изображение оказалось слева, а объект справа.

Ну так экрана же нету, поэтому от изображения $A'B'$ (неправильно наверное я терминологию "воображаемое" изображение использовал), лучи не будут идти на всю полусферу, а только внутри плоского угла $\theta$, а вот если экран поставить, тогда во все стороны! Вот тут мож я чего и не понял...

Dmitriy40 в сообщении #1439518 писал(а):

Расходиться они будут конечно во все стороны (если рассматривать не только лучи от далёкого объекта после объектива, они то в ограниченном угле), но те что не попадут в линзу объектива (или окуляра) нам не интересны, они поглотятся трубой телескопа и полезного действия не совершат. Но лучей мно-о-ого и какие-то попадут и в линзы — и они и построят нужное изображение. И даже их очень много (бесконечное количество, как возможных лучей в рамках заданного угла).

А допустим темнота, все кроме далекого объекта, опять же если поместить реальный объект (или экран) в фокальную плоскость объектива, то это будет уже не эквивалентно нашему изображению единственного объекта во Вселенной?

Dmitriy40 в сообщении #1439518 писал(а):

Это лучше понимать/разбираться с лупой, одиночной линзой, не с телескопом как (относительно) сложной оптической системой.
Возьмите тонкую собирающую линзу (с одним параметром фокусное расстояние), поместите объект на утроенном фокусном расстоянии, нарисуйте ход лучей. Потом на удвоенном. Потом на полуторном. Потом на 1.1 фокусного (можно и пропустить если уверены в своих силах). Заметьте что изображение всегда действительное, его можно увидеть на экране в данном месте. Потом точно на фокусном. Потом на 0.75 фокусного. В последнем случае должны получить расходящиеся лучи, справа нигде не пересекающиеся, т.е. изображения объекта не создающие. Но! Можно их продолжить влево за линзу, виртуально, пунктиром, и вот там они вполне себе пересекутся. И если бы справа был глаз (совершенно неважно как устроенный), то увидев такие расходящиеся лучи ему бы показалось что они идут от объекта слева где пересекаются их продолжения. Разумеется никакого объекта или изображения там нет, но глазу казалось бы что есть. И потому это кажущееся изображение называют мнимым. Заметьте что оно больше реального объекта, хотя и дальше от линзы. И не перевёрнутое относительно объекта. Если теперь построить угол под которым из некоей далёкой точки справа (дальше к примеру десятикратного фокусного расстояния) виден исходный объект без линзы и мнимое изображение через линзу, то будет видно что через линзу угол больше. Это и есть увеличение лупы.

Ага! Представил... Явное изображение это что-то где нам нужно, в той-же плоскости примерно, что-то разместить, например глаз или экран, а воображаемое изображение, это лучи света которые делают такой угловой размер как будто бы в точке где мы воображаем изображение оно действительно бы было, в смысле объект. Типа зеркала. И для этого не важна по сути система с которой мы будем разглядывать эти лучи. Это получается еще и потому, что в некотором угле очень много лучей, бесконечно много. Во, еще один пробел со школы уже не пробел в плане это все в уме представить.

Dmitriy40 в сообщении #1439518 писал(а):

Не надо ничего внутри линзы понимать. Летят и летят, и пусть летят как хотят. Главное что происходит с ними снаружи линзы. А снаружи Вы уже дважды построили картинку, для объектива. Переверните её так чтобы изображение было слева, а входные лучи справа, переназовите изображение объектом, лучи из него входными, лучи вправо после линзы выходными, а объект где-то справа далеко-далеко изображением — и будет Вам готовое решение почему лучи из фокальной плоскости уходят параллельными. Снова повторю, это просто свойство применяемых финтифлюшек под названием "линза", они специально именно так и сделаны.
Насчёт же воображаемого изображения, лучам после испускания уже без разницы чем или кем они испущены, хоть объектом, хоть звездой, хоть свечкой, хоть изображением чего-то, хоть реальным, хоть воображаемым — главное чтобы они хоть чем-то испустились, а дальше уже просто законы геометрической оптики (как очень маленького и сильно упрощённого кусочка физических законов, никакой магии или чудес тут нет).

Ну да, там другие участники форума печатали что линзы так специально делают, то есть я понял, специально чтобы если поместить объект в фокальной плоскости, от него лучи будут идти паралельно после линзы, и наоборот, если лучи идут параллельно, или по малым углом как в телескопе, они будут фокусироваться в фокальной плоскости (ну ошибка в плане телескопа неразличима), понял.

Dmitriy40 в сообщении #1439518 писал(а):

Не стоит пока в это лезть, рано, запутаетесь.
Коротко скажу, просто чтобы не оставлять в недоумении.
Дифракцию лучами да, неудобно, если вообще возможно, тут существенна волновая картина света, что в геометрической оптике игнорируется.
Аберрации можно и лучами, но неудобно, проще в терминах изображений и фокальных поверхностей (они уже не плоскости) и искажений поля зрения.
Надо понимать что это уже не идеальная геометрическая оптика, это уже следствие или физической природы света, или погрешностей изготовления оптических деталей (линз).

Да, моя интуиция не подвела по ходу снова, в смысле можно но неудобно. Спасибо! Не в дифракции пока не буду, там все сложно, когда в универе учился, точней "учился"... То мне эти механизмы дифракций, Фраунгоферы, Френели, и так далее, не особо понятные были, точней почти совсем непонятные... В любом случае когда-то повторю, выучу.

(arseniiv)

arseniiv в сообщении #1439554 писал(а):

Кроме того если начать строить ход лучей внутри линзы, придётся или мириться с тем, что она строго говоря уже не тонкая и ведёт себя хитрее, или придётся пренебрегать тем или сем, чем ТС по-моему заниматься упорно не хочет. Так до понимания дойти очень трудно, к тому же холизм вообще иллюзия, потому что мы не можем рассмотреть всех факторов в настоящих явлениях, и раз чем-то мы пренебрегаем даже просто потому что не знаем, что оно есть, то всё же неразумно не попренебрегать уже и сознательным образом. Но эта идея конечно не так проста и не сразу получает в голове одобрение. У меня когда-то в каких-то масштабах тоже такое было, но может быть потому что меня никто и не направлял, а тут ситуация вроде иная.

О, если это за свободу воли то я тоже в это верю! Как и во многое другое, хотя например такие как профессор Роберт Сапольський не верят, но например есть попытка научного подхода к этому от профессора Скотта Ааронсона, в его работе "The Ghost In The Qunatum Turring Machine" (2013), в честь годовщины Тьюрринга. Но лично мне конечно там ниче не понятно, просто говорю что и такое есть. И слова физика Альберта Айнштайна, про то "первый шаг не всегда может быть описан логикой", или как-то так, мне лично нравиться.

[Dmitriy40]

frostysh в сообщении #1439626 писал(а):

то как нам узнать радиус этой окружности чтобы потом узнать какую поправку внести у формулы чтобы было точней? Я подумаю над этим...

Ну там наверняка пригодится косинус угла ...

Рисунки с лупой детально до микрон сверять не буду, на первый взгляд правильно, за исключением случая 1.1F — для любого расположения объекта дальше фокуса лучи должны получаться сходящимися, а тут получились расходящиеся, что неправильно. UPD. Кажется они таки сходящиеся, только сильно далеко справа, тогда всё правильно.
Ещё полезное наблюдение: при расстоянии 2F изображение появляется точно на расстоянии 2F и точно такого же размера, только перевёрнутое.
Вариант с точно фокусным расстоянием не привели, а он может быть важен для понимания что происходит с параллельными лучами. Ведь это строго обратная ситуация для объектива телескопа.

(Другое объяснение работы телескопа, на пальцах)

Не хотел этого приводить, но может так будет проще понять. Вот есть лупа, можно с её помощью рассматривать предметы в увеличенном виде. Но далёкие предметы мы не можем рассмотреть в лупу т.к. не можем к ним приблизиться (просто по условиям). Но! Можем проделать финт ушами и приблизить изображение объекта к нам с лупой с помощью объектива. И тогда объектив создаст вот тут рядом изображение предмета и мы сможем его спокойно рассматривать в лупу. Получился телескоп. И не надо заморачиваться с ходом лучей от бесконечно удалённых предметов (точечные они там или нет). Правда это не позволяет посчитать увеличение или поле зрения или другие величины, но чисто интуитивно ... Впрочем некие оценки "на глаз" получить всё же можно: чем сильнее лупа (меньше её фокусное расстояние) тем больше её увеличение; чем длиннофокуснее объектив тем больше будет линейный размер изображения далёкого объекта; увеличивая фокус объектива и уменьшая фокус окуляра (лупы) увеличиваем суммарное увеличение телескопа. Но для вывода формулы придётся строить лучи.

[Xey]

К этому объяснению можно бы добавить картинку

Т.е. линза работает как совокупность призм с малым углом отклонения луча.
Такие призмы называют клиньями. Приближенная формула отклонения луча клином очень простая.
А точнее и не надо, геометрическая оптика описывает параксиальные лучи , идущие вблизи главной оси. Иначе изображение расползается.

Это расползание можно поправить асферическими поверхностями, но для лучей идущих под наклоном к оси асферические дают плохую картинку.

[frostysh]

Dmitriy40

Ах, да, я просто сонный был и у меня как всегда мысля не в ту сторону пошло. Используя рисунок выше и свойства прямоугольного треугольника можем найти следующий линейный размер изображение в фокальной плоскости объектива:

$$A'B' = 2F_{1}\tg{\dfrac{\theta}{2}},$$

направляя лучи в обратную сторону получим

$$\quad A'B' = 2F_{2}\tg{\dfrac{\varphi}{2}},$$

соответственно можем найти отношение тангенсов половинных углов

$$\dfrac{\tg{\dfrac{\varphi}{2}}}{\tg{\dfrac{\theta}{2}}} = \dfrac{F_{1}}{F_{2}}.$$

Теперь надо как-то связать отношение угловых размеров и отношение этих тангенсов половинных углов. Ладно, сегодня буду разбираться, потом. На счет рисунка с объектом в фокусе, да, пропустил почему-то, дорисую, пусть будет тоже. На счет телескопа как лупы тоже начинаю понимать, можно представить что там реальный объект в плоскости фокальной объектива, только перевернутый и по каких-то причинах от него идут лучи внутри некого угла, но это самого принципа работы телескопа никак не изменяет. Хорошо.

Xey

Создам отдельную тему поздней о том как лучи идут в линзах чтобы вообще спокойно на душе было в плане понимания этого, хотя-бы примерно, просто по какой-то причине не могу найти понятную книгу по этому, либо уровень университетов (у меня какие-то оптики есть), либо школьной (например учебник Барьяхтара), где этого нету. Ну думаю в интернете где-то есть.

П. С. Почему-то Латех ровняет тета в знаменателе не по нижней черточки дроби а по верхней, выглядит не очень, есть способы чтобы ровняло по нижней?

[Dmitriy40]

Вот чтобы не мучиться с половинными углами видимо и берут стрелочку/объект в одну сторону от оптической оси.

Кстати в русской вики вполне грамотно нарисованы ваши картинки и про линзу с выводом формул, и про систему линз, и про варианты расположения объекта: Ход лучей в тонкой линзе (этот пункт и все следующие до пункта "Недостатки простой линзы", его пока рано изучать, лишь ознакомиться при желании). Фактически эта викистатья полностью заменяет всю эту тему ... Зря товарищи сразу не послали туда чтобы здесь задавать уже конкретные вопросы что осталось непонятным в вики.
Разумеется всё это есть и в учебниках, но так как я не связан с преподаванием, то в каких не помню. Впрочем в самой вики есть ссылка на учебник, примечание 7 (сам не смотрел). Хотя, они сразу послали в школьный учебник, ну наверное там тоже есть все нужные выводы.

[frostysh]

Dmitriy40

Вот моя зарисовка для объекта разположеного перед линзой дальше на одну десятую фокусного расстояния этой линзы.



А вот для расположения объекта в фокусной плоскости.



На счет Википедии, я просто сначала начал разбирать механизм работы телескопа примерно с пункта в той статье "Расчет фокусного расстояния и оптической силы линзы", только для сильно упрощеного случая. Там просто дана уже формула с которой смысла мне особого нету ибо интересовало как-раз получения этого всего, то есть как это так получается что лучи именно туда идут и изображение строиться. А по поводу элементарных построений, так смысл мне у Википедию смотреть? Хотелось освежить память со школы, если сильно достал этот форум элементарными вопросами — то не знаю слова на русском, на украинской перепрошую.

[Dmitriy40]

Да, эти оба рисунка правильные.

Вот теперь возьмите последний рисунок, переверните его слева направо, чтобы лучи приходили из бесконечности параллельными — и они соберутся в фокальной плоскости в изображение объекта. Если там далеко-далеко объект мал, то угол между лучами от разных точек объекта (которые на данном рисунки идут параллельно оси и под углом к ней) будет очень мал и соответственно мал будет размер изображения. Но не нулевой для неточечного объекта.

Наверное пора Вам осмыслить последние рисунки, формулы, и попытаться чётко сформулировать что осталось непонятным.