Нет, можно сконструировать объект из разноцветных лазеров, выпускающих каждый ровно один луч в сторону линзы, всё равно правильное изображение будет лишь в фокальной плоскости (если объект в бесконечности), в остальных местах порядок цветов точек и их относительное расположение будут неправильными, т.е. изображение объекта будет искажённым.
Ну ведь тогда надо бесконечное количество этих лазеров или толстые лучи. Но я примерно понял, думаю что понял, что Вы подразумевали, — эти лучи за плоскостью будут пересекаться абы как. Но вот, следуя рекомендациям, допустим объект на расстоянии пару фокальных расстояний от объектива.
Если расстояние до объекта будет тысячу фокусных, или десять тысяч и при этом угловой размер линзы будет различимый с заданной точностью, то тогда и расстояние

, те есть разница между расстоянием где надо поставить экран чтобы изображение не размытое было и фокусным, должно быть различимо, мне вот интересно как это расстояние зависит от углового размера линзы если смотреть с объекта...
Будет мутное пятно.
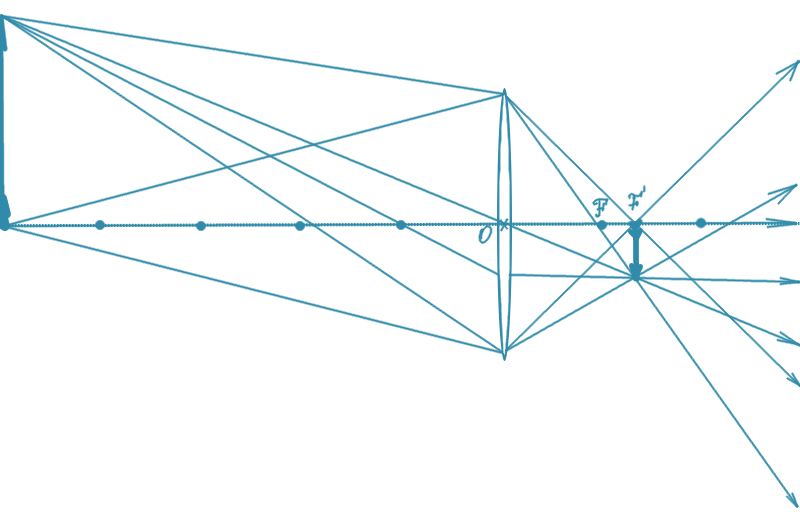
Чёткое изображение будет там, где пересекаются все лучи от одной точки объекта. А не от разных. Можно брать не все лучи, а несколько (минимум очевидно два, но лучше три, для контроля), один удобно пускать через центр линзы чтобы не считать как он преломляется (второй параллельно оптической оси — его можно сразу нарисовать за линзой через фокус, третий удобно пустить через передний фокус — тоже сразу понятно куда он пойдёт после линзы).
Да, спасибо! Сумел вообразить и представить.
По рисункам, у вас по моему слишком большой угол преломления на передней поверхности по сравнению с углом преломления задней, на тонкую линзу это совсем не похоже. Рисуйте точнее, показатели преломления стекла меньше полутора всего лишь, и уж точно одинаковы для передней и задней поверхности.
Ну вот так, только закон заломления то только для синусов, поэтому мы (ну то есть я) считаем что углы достаточно маленькие, но это не удобно рисовать...
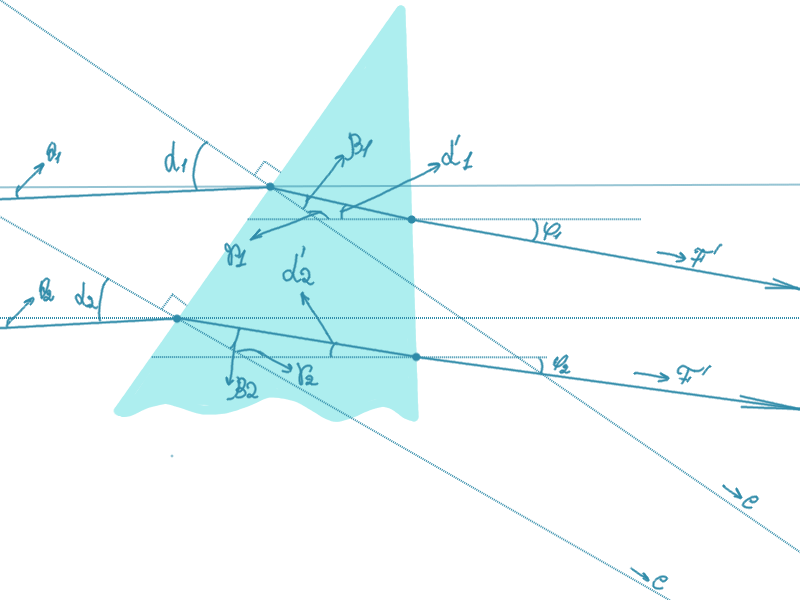
Удобно вместо плоской заднюю поверхность взять радиуса равным фокусному — при этом в идеале лучи ею преломляться не будут вообще, это проще для понимания и анализа.
Лучи не преломляються только когда есть симметрия, то есть луч иде сквозь центр оптический линзы, ну по крайней мере я так помню. Во вторых двовыпуклая линза мне сложная, в одновыпуклой хотя-бы понятно почему лучи параллельные фокальной оси в фокусе пересекутся, а з двовыпуклой формулы еще не разобрал и вообще представить сложно...
Честно говоря непонятно зачем погружаться в детали преломления внутри линзы если можно начать сразу с понятия тонкой линзы (у которой нулевая толщина и одна преломляющая поверхность). Строить ход лучей в ней, понять какие лучи удобно выбирать для быстрого построения изображения объекта. Разобраться с действительным и мнимым изображением (это важно). Потом добавить вторую тонкую же линзу и построить ход лучей уже в телескопе как единой конструкции. И смотреть где там спряталось увеличение.
Зачем разбираться сначала с линзами? — Не могу вообразить как оно там после объектива получается, и вообще как строиться изображение на экране, или на сетчатке, было сложно представить почему лучи от каждой отдельной точки параллельны на далеком расстоянии, а вот от разных точек объекта как бы и нет, это наверное самое сложное было, но как оказалось это зависит от размера линзы объектива и объекта, то есть от их угловых размеров приблизительно, и это стало понятным после рисунков и пару формул.
Тут, мне кажется, не надо путать причину и следствие. Собирающие линзы специально делают именно так, чтобы лучи, параллельные оптической оси, пересекались в одной точке. И уже из этого следует их (линз) нужная форма и остальные геометро-оптические свойства.
Я понятия не имею как делают линзы, но недавно узнал что для тоненькой (но достаточно толстой), одновыпуклой линзы, угол между главной фокусной осью зависит от угла падания лучей параллельных главной фокусной оси пропорционально, это значит что любое изменения угла падения (из-за сферичности линзы) влечет за собою изменение угла между уже заломленым лучом и осью, поэтому все лучи в одно точке фокусируются. Для двовыпуклой линзы сложней но тоже самое, еще не разобрался.
Причем коэффициент пропорциональности постоянен и зависит от коэффициента преломления из внешней среды в линзу.
arseniivХотя бы потому-что это помогло мне понять, представить, что не параллельные лучи идут от объекта, а только от точки на объекте, причем по сути непараллельные и там и там, просто первая непараллельность в много-много раз (если только линза не размером с объект) больше второй... Объект имеет угловой размер, если объект не имеет углового размера в телескопе (то есть имеет нулевой, это более математично а не физично думаю), то смысла на него смотреть нету в плане увеличения в этот телескоп!