Допустим, в алгебре я могу постепенно, шаг за шагом переходить от

, к более сложным

и далее, без скачков к уравнениям

степеней. Есть определенная преемственность. А здесь получается, что вот вполне понятная запись

, а потом внезапно появляется

или

, которые непонятно что. Переменные? Множества? Дельты некоторых изменений функции? Значения скорости изменения функции?
Ну давайте немного философии.
1. В алгебре вы работаете с числами. Вы осваиваете операции (алгебраические операции):
сложение, умножение, вычитание, деление
и их свойства. Чтобы говорить о каких-то общих случаях, вы заменяете числа буквами, и переходите к действиям с буквами. Например, вы можете начать с выражения

и раскрыть скобки, но не можете вычислить его значение до окончательного числа, потому что вам не известно, что надо подставлять в буквы

и
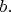
То есть, вы работаете с формулами из чисел и букв (которые тоже подразумевают числа). И наконец, вы можете поставить задачу: "такая-то формула даёт такое-то число; какие числа в неё подставлены?". То есть, записать уравнение, и начать решать его относительно неизвестных значений букв. Такое уравнение - алгебраическое уравнение - тоже даёт в ответе число.
2. В мат. анализе вы работаете с функциями. Функция - это объект более сложный, чем число, он содержит больше информации. Соответственно, с ними есть тоже множество разных действий, операций. Часть этих действий в школе называют "действия над графиками".
а) Есть поточечные операции с числами ("по-точечные", то есть "по точкам"). Это такие же действия, что и обычные алгебраические операции, они записываются такими же значками. Но смысл здесь таков, что берётся функция и функция, и на выходе в результате получается снова функция:
 - это означает "в каждой точке
- это означает "в каждой точке  то есть, при каждом значении независимой переменной
то есть, при каждом значении независимой переменной  надо сначала вычислить значение функции
надо сначала вычислить значение функции  а потом значение функции
а потом значение функции  и их сложить - и это будет значение новой функции в той же точке
и их сложить - и это будет значение новой функции в той же точке  ";
";
 - это означает "в каждой точке
- это означает "в каждой точке  надо сначала вычислить значение функции
надо сначала вычислить значение функции  а потом умножить его на
а потом умножить его на  - и это будет значение новой функции в той же точке
- и это будет значение новой функции в той же точке  ".
".
б) Есть алгебраические операции, но уже не поточечные. Например:
 - это означает "в каждой точке
- это означает "в каждой точке  надо сначала сложить
надо сначала сложить  и получить новое число, а потом вычислить значение функции
и получить новое число, а потом вычислить значение функции  уже для этого нового числа как независимой переменной - и это будет значение новой функции именно в точке
уже для этого нового числа как независимой переменной - и это будет значение новой функции именно в точке  ".
".
Этими действиями можно, например, совершать множество действий с графиками функций: сдвигать по вертикали и по горизонтали, сжимать и растягивать, отражать, и т. д.
в) Обобщение предыдущей идеи - это общая идея
замены переменных, или
подстановки функции в функцию, или
операции композиции функций. А именно:
 - это означает "в каждой точке
- это означает "в каждой точке  то есть, при каждом значении независимой переменной
то есть, при каждом значении независимой переменной  надо сначала вычислить значение функции
надо сначала вычислить значение функции  а вычислить значение функции
а вычислить значение функции  уже для этого нового числа как независимой переменной - и это будет значение новой функции, опять же, именно в точке
уже для этого нового числа как независимой переменной - и это будет значение новой функции, опять же, именно в точке  ".
".
Операция композиции уже позволяет очень мощно конструировать разнообразные функции, но ей не хватает маленькой детали. Спросим себя, если

- какая-то известная функция, то какой должна быть неизвестная функция

чтобы выполнялось

? То есть, такая функция будет как бы "отменять" действие функции

г) Операция взятия обратной функции - это такая функция

что выполняется

и

Обратная функция бывает не для всякой функции

Зато если уж она есть, то

- то есть, данная функция будет обратной к своей обратной. Несколько примеров обратных функций:
![$\sqrt[n]{x}$ $\sqrt[n]{x}$](https://dxdy-03.korotkov.co.uk/f/6/3/f/63fb778ee723673461d37510bb35cba782.png) - функция, обратная к
- функция, обратная к  (если мы не ограничим область определения для функции возведения в степень, то у неё может не быть обратной);
(если мы не ограничим область определения для функции возведения в степень, то у неё может не быть обратной);
 - функция, обратная к
- функция, обратная к  ;
;
 - функция, обратная к
- функция, обратная к ![$\sin x,x\in[-\tfrac{\pi}{2},\tfrac{\pi}{2}]$ $\sin x,x\in[-\tfrac{\pi}{2},\tfrac{\pi}{2}]$](https://dxdy-02.korotkov.co.uk/f/5/5/1/551996969b0e6c2a65555afd482ba3c882.png) (если мы не ограничим достаточно область определения для функции синуса, то у неё не будет обратной)...
(если мы не ограничим достаточно область определения для функции синуса, то у неё не будет обратной)...
Итак, в этой области

- это какая-то конкретная функция, а буквами

обозначаются такие функции, которые ещё не известны, но на их место можно подставлять всякие разные функции (не всегда любые; например, к функции могут быть какие-то требования). И наконец, можно записать
функциональное уравнение, то есть такое, в котором некоторая буква

- неизвестная функция, а само уравнение при помощи каких-то операций с ней - выражает какое-то свойство этой функции. (Или система уравнений и несколько функций.) Например:
 - такому уравнению удовлетворяет показательная функция
- такому уравнению удовлетворяет показательная функция 
Но всё-таки в таком виде это довольно "скучный" мир (а функциональные уравнения почти все безнадёжно нерешаемы), и недостаточен для надобностей физики и техники. И поэтому в него добавляют ещё
д) Операции дифференцирования и интегрирования. Они выходят за рамки вычисления функций в отдельных точках, и требуют:
чтобы узнать значение производной от данной функции - знать её значения в какой-то окрестности точки, справа и слева;
а чтобы узнать значение интеграла от данной функции - знать её значения на каком-то большом промежутке, например, слева от данной точки.
Это не единственные операции такого типа, но с них можно начинать. (Например, есть важные операции свёртки; преобразования Фурье; преобразования Лапласа.)
И уже эти операции позволяют записывать
дифференциальные и
интегральные уравнения, которые не только часто удачно решаются, но и выражают очень многие идеи и математические модели в физике и других науках. Например:
 выражает идею, что какое-то количество
выражает идею, что какое-то количество  постоянно уменьшается, причём со скоростью, пропорциональной самому этому количеству, например, скорость радиоактивного распада пропорциональна количеству радиоактивного вещества (а единица вещества распадается с одной и той же скоростью, не меняющейся по времени и от других условий);
постоянно уменьшается, причём со скоростью, пропорциональной самому этому количеству, например, скорость радиоактивного распада пропорциональна количеству радиоактивного вещества (а единица вещества распадается с одной и той же скоростью, не меняющейся по времени и от других условий);
и решение этого уравнения  является законом радиоактивного полураспада, с периодом полураспада, равным
является законом радиоактивного полураспада, с периодом полураспада, равным 
То есть, вам надо освоить один новый объект - функции. И две новых операции: дифференцирование и интегрирование. Но конечно, это в сумме довольно много новых фактов, и осваивать вы их будете долго и постепенно.



