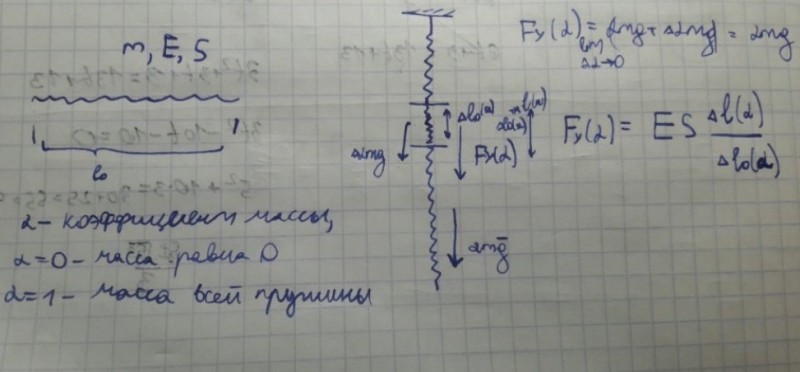
Сегодня на дне открытых дверей в МФТИ студенты ФОПФ раздавали листочки с условиями задач. Там была задача с висящей пружиной. Данная задача сводилась к следующей вспомогательной: Пусть дана вертикально висящая пружина с жесткостью
![$\[k = \frac{{ES}}{{{l_0}}}\]$ $\[k = \frac{{ES}}{{{l_0}}}\]$](https://dxdy-02.korotkov.co.uk/f/d/f/a/dfa662a5733730d2b1f942c0b582575a82.png)
, и равномерно распределенной массой

. Необходимо найти удлинение пружины под действием силы тяжести.
Мое решение, как по мне, является весьма громоздким, и воспроизводить подобное на олимпиадах не самый лучший вариант - время ограничено. Прошу форумчан посоветовать, что можно изменить в моем решении, чтобы как можно быстрее прийти к тому же результату. Буду рад и другим вариантам решения.
Для начала ввожу коэффициент массы
![$\[\alpha \]$ $\[\alpha \]$](https://dxdy-03.korotkov.co.uk/f/a/0/b/a0b2054e7bad2f2818e3ff801fa7a41882.png)
для параметризации пружины: он отчитывает часть массы пружины, рассматриваемой от самой низшей точки пружины до точки, определяемой данным параметром.Если
![$\[\alpha = 0\]$ $\[\alpha = 0\]$](https://dxdy-04.korotkov.co.uk/f/3/c/c/3cc913a20917e043ef63ad76f60a43a182.png)
, то рассматриваемая часть пружины вырождается в низшую точку всей пружины, если
![$\[\alpha = 1\]$ $\[\alpha = 1\]$](https://dxdy-01.korotkov.co.uk/f/4/6/8/468d01b98b9a3cd729261936bbbd078982.png)
, то имеем дело со всей пружиной, таким образом,
![$\[\alpha \in \left[ {0;1} \right]\]$ $\[\alpha \in \left[ {0;1} \right]\]$](https://dxdy-02.korotkov.co.uk/f/9/a/d/9ad253e5951a09018aa8057f59b76f3b82.png)
.
Рассмотрим малую часть пружины длиной
![$\[\Delta {l_0}(\alpha )\]$ $\[\Delta {l_0}(\alpha )\]$](https://dxdy-01.korotkov.co.uk/f/4/f/3/4f33a90ea60e895ecdc09f841ba77c1682.png)
в недеформированном состоянии, находящуюся выше части пружины массой
![$\[\alpha mg\]$ $\[\alpha mg\]$](https://dxdy-04.korotkov.co.uk/f/f/a/c/facde5416a4eb160e5a417085b2841cd82.png)
. Пусть
![$\[\Delta l(\alpha )\]$ $\[\Delta l(\alpha )\]$](https://dxdy-03.korotkov.co.uk/f/e/5/e/e5ebb2433f1fdf39773702e3c37c9e9082.png)
- удлинение малой части пружины вследствие действия силы тяжести. Введем коэффициент удлинения
![$\[t(\alpha ) = \frac{{\Delta l(\alpha ) + \Delta {l_0}(\alpha )}}{{\Delta l(\alpha )}}\]$ $\[t(\alpha ) = \frac{{\Delta l(\alpha ) + \Delta {l_0}(\alpha )}}{{\Delta l(\alpha )}}\]$](https://dxdy-04.korotkov.co.uk/f/f/e/9/fe98353c40ee878b3dade78d662181c382.png)
. Во второму закону Ньютона и закону Гука имеем:
![$$\[\alpha mg = ES\frac{{\Delta {l_0}(\alpha )}}{{\Delta l(\alpha )}} = ES\left( {t - 1} \right) \Rightarrow t(\alpha ) = \alpha \frac{{mg}}{{ES}} + 1\]$$ $$\[\alpha mg = ES\frac{{\Delta {l_0}(\alpha )}}{{\Delta l(\alpha )}} = ES\left( {t - 1} \right) \Rightarrow t(\alpha ) = \alpha \frac{{mg}}{{ES}} + 1\]$$](https://dxdy-03.korotkov.co.uk/f/a/e/5/ae55819ad1bc39b1c080f1ff75c5d1cf82.png)
Элементарное длина малой части пружины в деформированном состоянии равна
![$\[t(\alpha )\Delta {l_0}(\alpha )\]$ $\[t(\alpha )\Delta {l_0}(\alpha )\]$](https://dxdy-02.korotkov.co.uk/f/5/6/e/56eef5e23b264bed0d555bdc553dc8f882.png)
, тогда общая длина равна:
![$$\[l = \sum {t(\alpha )\Delta {l_0}(\alpha ) = } \sum {\left( {\alpha \frac{{mg}}{{ES}} + 1} \right)\Delta {l_0}(\alpha ) = } \sum {\Delta {l_0}(\alpha ) + \sum {\alpha \Delta {l_0}(\alpha )\frac{{mg}}{{ES}}} } = {l_0} + \frac{1}{2}\frac{{mg}}{{ES}} \cdot {l_0} = {l_0} + \frac{1}{2}\frac{{mg}}{k}\]$$ $$\[l = \sum {t(\alpha )\Delta {l_0}(\alpha ) = } \sum {\left( {\alpha \frac{{mg}}{{ES}} + 1} \right)\Delta {l_0}(\alpha ) = } \sum {\Delta {l_0}(\alpha ) + \sum {\alpha \Delta {l_0}(\alpha )\frac{{mg}}{{ES}}} } = {l_0} + \frac{1}{2}\frac{{mg}}{{ES}} \cdot {l_0} = {l_0} + \frac{1}{2}\frac{{mg}}{k}\]$$](https://dxdy-03.korotkov.co.uk/f/6/6/2/6621cdbc593598084c909e1e581d707d82.png)
Последние выкладки опираются на тот факт, что
![$$\[\sum {\alpha \Delta {l_0}(\alpha ) = \frac{{{l_0}}}{2}} \]$$ $$\[\sum {\alpha \Delta {l_0}(\alpha ) = \frac{{{l_0}}}{2}} \]$$](https://dxdy-03.korotkov.co.uk/f/e/b/0/eb0eccbfef1bf70a86aa1834d961616282.png)
, я понятия не имею, как это доказать.
Хотелось бы для начала посоветоваться по поводу того,во-первых ,почему
![$$\[\sum {\alpha \Delta {l_0}(\alpha ) = \frac{{{l_0}}}{2}} \]$$ $$\[\sum {\alpha \Delta {l_0}(\alpha ) = \frac{{{l_0}}}{2}} \]$$](https://dxdy-03.korotkov.co.uk/f/e/b/0/eb0eccbfef1bf70a86aa1834d961616282.png)
дабы разобраться с моим решением и, во-вторых, интересно было бы услышать предложения по поводу альтернативных решений.
-- 08.01.2019, 19:12 --Похоже с суммой разобрался:
![$$\[\int\limits_0^1 {\alpha d{l_0} = } \int\limits_0^1 {\alpha {l_0}d\alpha = {l_0}} \int\limits_0^1 {\alpha d\alpha = } \frac{{{l_0}}}{2}\]$$ $$\[\int\limits_0^1 {\alpha d{l_0} = } \int\limits_0^1 {\alpha {l_0}d\alpha = {l_0}} \int\limits_0^1 {\alpha d\alpha = } \frac{{{l_0}}}{2}\]$$](https://dxdy-04.korotkov.co.uk/f/3/4/2/34288baf344279ce025cbb9b9d7258ac82.png)
Вопрос с альтернативным решением остается открытый.



