Для школьников в этой задаче я вижу три сложности.
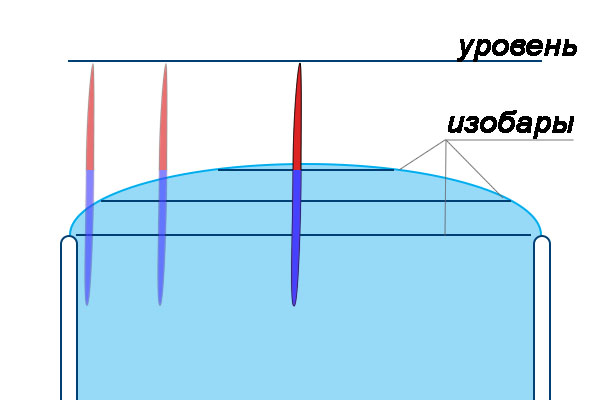
1. Нарушение закона Архимеда из-за того, что он справедлив только для горизонтального уровня жидкости, которое иллюстрируется рисунком.
Изобары - линии равного давления в жидкости соответствуют линиям mgh, а сверху условно показан равновесный уровень поплавка.
2. В зависимости от угла смачивания поплавка жидкостью, изменяется величина и знак работы, совершаемой поверхностным натяжением на единицу длины смоченного периметра поплавка.
3. При изменении положения плавающего тела с переменным сечением, длина смоченного периметра изменяется.
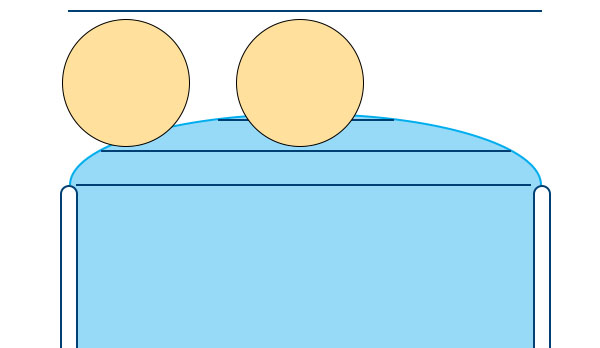
Теперь очевидно, что результат зависит как от смачиваемости тела, так и от формы его поверхности.
Если величина смоченного периметра тела при смещении к краю сосуда уменьшается и поверхность тела смачиваемая, то его энергия увеличивается - тело самопроизвольно вернется в положение с максимальным смоченным периметром.
Если мы возьмем тело в виде конуса с верхним положением вершины, то величина смоченного периметра при смещении к краю увеличится - смачиваемое тело будет стремиться к краю сосуда.
Если тело не смачивается жидкостью, то в двух вариантах выше, результат будет противоположным.
Если поплавок цилиндрический, то на краю сосуда его сечение поверхностью жидкости превратится из окружности в овал (увеличится), то есть он поведет себя как шарик, погруженный менее чем на половину - будет стремится к центру если смачивается и к краю - если не смачивается.



