Тема навеяна сообщениями
manul91 и
epros в
topic130678-75.htmlПусть мы произвольно задали микросостояние какой-то системы, и соответственно определили ее макросостояние. Система начала эволюционировать с соответствующем увеличением энтропии с условного момента
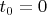
когда мы ее приготовили в этом состоянии. Но если мы начнем ее эволюционировать назад во времени

, путем обращения назад обратимых физических законов взаимодействий частиц, то энтропия будет тоже
увеличиваться, и соответственно в прямом времени уменьшаться. Т.е. мы задали точку отсчета на оси времени, создав данное микросостояние, а затем энтропия начала увеличиваться в обе стороны от него, задавая как бы два направления времени.
Это легко видеть на примере диффузии, пусть у нас есть неравномерное распределение каких-то частиц на кольце, каждая частица может с равной вероятностью сместиться и влево и вправо. Очевидно что система придет в равновесное положение, когда плотность частиц везде будет одинаковой. НО! Если мы обратим эту систему назад во времени, то закон случайного блуждания не поменяется, просто поменяется лево и право, а сам закон останется тем же. Получается энтропия должна увеличиваться и при обратном времени от точки задания начального состояния системы!
Кто что думает по этому вопросу?



