===========ММ239===============ММ239 (10 баллов)
Существует ли выпуклый многогранник, у которого:
a) не менее половины граней семиугольники;
b) более половины граней семиугольники;
с) не менее половины граней восьмиугольники;
d) более половины граней восьмиугольники;
e) не менее половины граней девятиугольники?
Примечание: Если у вас получается, что ответ на пункт <а> отрицательный, а на пункт <b> - положительный, подумайте еще.
РешениеПривожу решения Виктора Филимоненкова, Анатолия Казмерчука, Владимира Чубанова и vpb.
(Решение Владимира Чубанова)
ММ239Существует ли выпуклый многогранник, у которого:
a) не менее половины граней семиугольники;
b) более половины граней семиугольники;
с) не менее половины граней восьмиугольники;
d) более половины граней восьмиугольники;
e) не менее половины граней девятиугольники?
Эстетическая оценка 5 баллов. Мне нравятся такие задачи, правда, эта сильно пересекается с позапрошлым марафоном.
__________
Ответы: a) -- d) да, e) нет.
Решение.
Решение основано на уже упоминавшемся в марафонах неравенстве

Здесь

-- число

-угольных граней. Равенство получается с применением формулы Эйлера при подсчёте рёбер, вершин и граней простого многогранника (в каждой вершине которого сходится 3 ребра). Если в какой-то из вершин сходится более трёх рёбер, равенство превращается в неравенство. Вывод (1) я не буду давать, поскольку и я, и другие участники уже давали его в одном из прошлых марафонов.
Сразу заметим, что данное неравенство очевидно несовместимо с п. e). С остальными пунктами противоречий нет и результат можно получить из теоремы Эберхарда, но лучше построить подтверждающие примеры.
Для п. a) дадим простой умозрительный пример: обрежем немного все вершины куба, кроме двух диагональных. Тогда все 6 граней куба станут 7-угольными и добавится ещё 6 треугольных граней. В этом случае неравенство (1) становится равенством и можно заметить, что многогранник с меньшим (меньше 12) количеством граней не может удовлетворять п. a).
Для п. b) приведём ещё один явный пример. На рисунке ниже кружочки обозначают место среза вершины, образующее 3-угольную грань. Количество 7-угольных граней в данном примере равно 15, количество 3-угольных -- 11, и 6-угольных -- 3.

Для п.п. c) и d) приведём один пример. Многогранник на рисунке получен пересечением двух 8-угольных пирамид. Если каждую вершину в нём немного обрезать плоскостью, как в примере выше, получим

8-угольных граней и 16 треугольных.

Для произвольных

максимально возможную долю

в общем количестве граней легко можно вычислить, используя теорему Эберхарда, утверждающую, что существует простой многогранник для любого набора

, удовлетворяющего равенству в (1). Следовательно, (недостижимый) супремум возможной доли

составляет

. Для

супремум равен 1 (на последовательности фуллеренов, которые могут иметь произвольно большое количество 6-угольных граней при 12 пятиугольных). При

существуют многогранники, имеющие только

-угольные грани.
(Решение vpb)
ММ239Для выпуклого многогранника

и натурального числа

пусть

--- отношение числа граней

, являющихся

-угольниками, к общему числу граней.
Ответ на все пункты задачи содержится в следующей теореме.
Теорема. Для любого  и любого
и любого  верно неравенство
верно неравенство  . В случае
. В случае  число
число  является точной верхней гранью для
является точной верхней гранью для  , по всем
, по всем  (которая, таким образом, не достигается).
(которая, таким образом, не достигается). Отсюда ответы на пункты а)--г) задачи положительны, на д) отрицательный.
Сначала докажем первое утверждение теоремы.
Предложение. Всегда  , при
, при  . Доказательство.
. Доказательство. Обозначим

. Пусть

,

,

--- числа вершин, ребер, граней соответственно. По формуле Эйлера

. Также

.
Оценим

. Имеем

, где

--- число

-угольников,

--- прочих граней. Таким образом,

,

. Ясно, что

, откуда

Значит

. Подставляя оценки для

и

в формулу Эйлера, находим

, откуда

,

,

,

,

.
QED
Для доказательства второго утверждения сначала рассмотрим некоторый "многогранник" на плоскости (т.е. разбиение плоскости на выпуклые многоугольники).
Пусть

--- некоторая плоскость. Пусть

--- (однозначно определенное
с точностью до движения) разбиение плоскости на правильные 6-угольники с ребром длины

.
Пусть

--- множество всех вершин

.
Лемма. Для каждого  существует такое подмножество
существует такое подмножество  , что ровно
, что ровно  вершин каждого шестиугольника из
вершин каждого шестиугольника из  принадлежат
принадлежат  . Доказательство.
. Доказательство. При

, очевидно,

,

. При

предоставляем найти

читателю, нарисовав картинку (

будет периодическим). При

можно взять в качестве

дополнения

,

соответственно. QED
Для

определим некоторое разбиение плоскости на треугольники и (неправильные)

-угольники (неправильные), обозначим его

. Именно, возьмем разбиение

, и каждую вершину

(где

) заменим на небольшой треугольник (детальное описание такой замены опустим).
Ясно, что в разбиении

каждый

-угольник граничит с

треугольниками, а каждый треугольник с тремя

-угольниками. Поэтому асимптотическое отношение числа

-угольников к числу треугольников составляет

. "Асимптотическое" означает, что если мы возьмем окружность достаточно большого радиуса

, и ограничимся рассмотрением тех многоугольников разбиения, которые целиком лежат внутри окружности, то указанное отношение стремится к

, когда

. Поэтому доля

-угольников среди всех граней разбиения стремится к

, что и нужно.
Теперь надо "перенести" описанную конструкцию в пространство. Будем считать плоскость

вложенной в обычное трехмерное евклидово пространство. Возьмем какую-либо сферу, касающуюся

, обозначим ее

. Пусть

--- точка касания,

--- противоположная точка сферы ("южный" и "северный" полюса). Пусть

--- (обратная) стереографическая проекция, т.е.

--- это точка пересечения

с отрезком

, для любой

. Хорошо известно, что при стереографической проекции окружности на плоскости соответствуют окружностям на сфере.
Пусть

--- круг радиуса

с центром в

;

--- образы на сфере тех точек из

, которые лежат в

. Наконец, пусть

--- выпуклая оболочка

в пространстве.
Лемма. Пусть  --- некоторый шестиугольник разбиения
--- некоторый шестиугольник разбиения  такой, что
такой, что  ;
;
 --- его вершины, и
--- его вершины, и  . Тогда
. Тогда  лежат в одной плоскости, и
лежат в одной плоскости, и  --- грань для
--- грань для  , причем
, причем  --- вершины этой грани. Доказательство.
--- вершины этой грани. Доказательство. 
--- правильный шестиугольник, значит он вписан в некоторую окружность

.

--- окружность на

, значит, лежит в некоторой плоскости

. Значит, все

.
Плоскость

делит

на две части, а именно, внутренность и внешность окружности

. Соответствующие части на

--- это внутренность и внешность окружности

. Однако ни одна вершина из

не лежит внутри

. Значит, все вершины из

, и тем более

, лежат по одну сторону от

. При этом на

лежат только

. Значит, их выпуклая оболочка --- это грань многогранника

(и сами они --- в точности вершины этой грани).
QED
В ситуации, описанной в лемме, будем обозначать

через

.
Следствие. Пусть  . Тогда грани в
. Тогда грани в  , содержащие
, содержащие  --- это три шестиугольника (и других граней нет). Доказательство.
--- это три шестиугольника (и других граней нет). Доказательство. Пусть

,

,
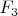
--- три шестиугольника

, содержащие

. Тогда все они лежат внутри

. Значит

--- грань для

, содержащая

. Поскольку

и

имеют общее ребро, то

и

имеют общее ребро. Но, поскольку каждые две из трех граней

имеют общее ребро, других граней, содержащих

, нет. QED
Таким образом, мы видим, что в окрестности всех вершин, за исключением вершин

, для которых

,

устроено комбинаторно так же, как

. Всего

имеет порядка

вершин, ребер и граней. А "исключительных" вершин, очевидно, порядка

(откуда легко следует, что "нехороших" ребер и граней тоже

).
Теперь мы усечем многогранник

в окрестностях некоторых вершин. А именно, в окрестностях вершин

, для которых

. Довольно понятно, что полученный многогранник содержит столько же

-угольников и треугольников, сколько разбиение

внутри круга

, с точностью до

. А также, возможно, есть

других граней, кроме треугольников и

-угольников. Отсюда следует, что

, чем теорема и доказана.
QED
Обсуждение Ровно в половине всех присланных (и всех приведенных) решений авторы обошлись без картининок.
Чтобы восполнить этот пробел, приведу пару своих картинок (зря, чтоли рисовал?).
Первый рисунок иллюстрирует ответы сразу к трем пунктам задачи: a), b), c).
Отрезав от додекаэдра красные вершины, получим многогранник в котором более (а значит, и не менее) половины граней являются семиугольниками.
Если же наоборот, оставить красные вершины, а остальные отрезать, получим многогранник, в котором ровно половина граней - восьмиугольники.

На втором рисунке приведен граф многогранника с вектором граней (28,0,0,4,0,36), обосновывающий положительный ответ к пункту d).

ММ239 (как и ММ235) - это отголосок XXII Марафонского конкурса, посвященного данной тематике. Участники, пропустившие тот конкурс, вынуждены были переотрывать утверждения типа Теоремы Эберхарда etc (конечно, можно было просто найти нужные результаты в сети, но наши конкурсанты не ищут легких путей

). С удовольствием констатирую, что нашлись те, кто преодолел эти трудности (были ли те, кто не смог - неизвестно, они решений не прислали).
Изучение вопроса о верхней грани отношения количества k-угольных граней к общему числу граней (

) поощрялось дополнительными баллами. В случае
vpb, это поощрение скомпенсировалось сбавкой за штейнеровское отношение к читателю

. (Каюсь, сам я работ Якоба Штейнера в первоисточнике не читал, но, говорят, он свои сугубо геометрические выкладки вообще не снабжал чертежами.)
Остальные изъятия сделаны либо за отсутствие примеров на некоторые пункты, либо за присутствие примеров с невозможными многогранниками (с нецелым количеством ребер

)
Волшебное превращение восьмиугольных граней в семиугольные (при склейке по общей треугольной грани) я оценивать не стал
 Награды
НаградыЗа решение задачи ММ239 участники Марафона получают следующие призовые баллы:
Анатолий Казмерчук - 12;
Владимир Чубанов - 11;
vpb - 10;
Константин Шамсутдинов - 10;
Виктор Филимоненков - 9;
Владислав Франк - 6.
Эстетическая оценка задачи - 4.8 балла