===========ММ236===============ММ236 (7 баллов)
Натуральные числа от 1 до
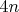
разбили на четыре группы по

чисел в каждой. Оказалось, что произведение всех чисел из первой группы равно произведениям всех чисел из второй и третьей групп. Найти наименьшую возможную сумму чисел четвертой группы.Существует ли выпуклый многогранник, у которого равны: количество ребер; количество диагоналей; суммарное количество диагоналей граней?
РешениеПривожу решения Виктора Филимоненкова (мне понравилось его доказательство минимальности ответа), Юрия Варламова (с принципиально иным подходом к доказательству минимальности) и Анатолия Казмерчука (с хорошей оценкой на подходящие

для обобщения задачи).
Обсуждение Наиболее сложной частью решения данной задачи оказалось внимательное прочтение условия. Сразу три конкурсанта решали другую задачу, в которой произведение чисел первой группы равнялось не произедениЯМ чисел из второй и третьей групп, а произведениЮ этих произведений. Причем один из них не "исправился" даже после явного указания на этот момент.
Основным недочетом решения было недостаточно строгое обоснование минимальности найденного ответа. Лично меня вполне убеждает реплика типа "ясно, что с дальнейшим ростом

сумма чисел в 4-й группе будет возрастать". Но балл я, все таки, снимал. Тем более, что я не вовсе не уверен в монотонности этого роста.
Другие неточности были связаны с тем, что один из конкурсантов "прозевал" требуемое разбиение для

и нашел его только для

, а другой наоборот не заметил разбиения для

. Последнее, правда, вовсе и не требовалось (при наличии разбиения для

), но это не повод, чтобы утверждать, что его нет

Задача просто напрашивается на обобщения. Выражу эти обобщения в виде двух предположений:
1. Для любого натурального

найдется натуральное

такое, что числа от 1 до

, можно разбить на

групп по

чисел так, что произведения чисел во всех группах, за исключением одной, будут одинаковы.
2. Для любого натурального

найдется натуральное

такое, что для любого натурального

числа от 1 до

, можно разбить на

групп по

чисел так, что произведения чисел во всех группах, за исключением одной, будут одинаковы.
Тех конкурсантов, которые высказали подобные гипотезы, я поощрял дополнительным призовым баллом. Еще одним баллом поощрялись оценки снизу для подходящих

для разных количеств групп. Разглядеть следы этих поощрений в разделе "Награды" можно не всегда, поскольку они в значительной мере скомпенсировались штрафами за отмеченные выше недостатки.
Подтвердить первое утверждение мне удалось пока лишь для

. Подходящее

оказалось равно 440. Оно хорошо согласуется с оценкой из решения Анатолия и, по-видимому, является минимальным.
В особую группу в этом случае можно включить числа:
47, 59, 71, 73, 79, 83, 97, 101, 103, 113, 127, 139, 149, 151, 157, 158, 163, 167, 191, 193, 194, 197, 199, 211, 223, 226, 227, 229, 233, 239, 241, 277, 278, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 382, 383, 386, 389, 394, 397, 398, 401, 409, 417, 419, 421, 422, 431, 433, 439, 554, 557, 562, 563, 566, 569, 571, 573, 577, 586, 587, 593, 599, 601, 607, 613, 614, 617, 619, 622, 625, 626, 631, 634, 641, 643, 647, 653, 659, 661, 662, 673, 674, 677, 683, 691, 694, 698, 701, 709, 719, 727, 729, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 831, 839, 843, 849, 853, 857, 859, 863, 877, 879, 881, 883, 887, 907, 911, 919, 921, 929, 933, 937, 939, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1059, 1061, 1063, 1069, 1077, 1087, 1091, 1093, 1097, 1103, 1109, 1114, 1117, 1123, 1126, 1129, 1138, 1142, 1151, 1153, 1154, 1163, 1171, 1174, 1181, 1186, 1187, 1193, 1198, 1201, 1202, 1213, 1214, 1217, 1223, 1226, 1229, 1231, 1234, 1237, 1238, 1249, 1259, 1262, 1277, 1279, 1282, 1283, 1286, 1289, 1291, 1294, 1297, 1301, 1303, 1306, 1307, 1318, 1319, 1321, 1322, 1327, 1346, 1354, 1361, 1366, 1367, 1373, 1381, 1382, 1399, 1402, 1409, 1418, 1423, 1427, 1429, 1433, 1438, 1439, 1447, 1451, 1453, 1454, 1459, 1466, 1471, 1478, 1481, 1483, 1486, 1487, 1489, 1493, 1499, 1502, 1511, 1514, 1522, 1523, 1531, 1538, 1543, 1546, 1549, 1553, 1559, 1567, 1571, 1574, 1579, 1583, 1594, 1597, 1601, 1607, 1609, 1613, 1618, 1619, 1621, 1622, 1627, 1637, 1642, 1646, 1654, 1657, 1658, 1663, 1667, 1669, 1671, 1678, 1679, 1689, 1693, 1697, 1699, 1706, 1707, 1709, 1713, 1714, 1718, 1721, 1723, 1726, 1731, 1733, 1741, 1747, 1753, 1754, 1759, 1761, 1762, 1766, 1774, 1777, 1779, 1783, 1787, 1789, 1797, 1801, 1803, 1811, 1814, 1817, 1821, 1822, 1823, 1831, 1838, 1839, 1847, 1851, 1857, 1858, 1861, 1867, 1871, 1873, 1874, 1877, 1879, 1882, 1889, 1893, 1894, 1901, 1906, 1907, 1909, 1913, 1923, 1927, 1929, 1931, 1933, 1934, 1937, 1941, 1942, 1949, 1951, 1954, 1959, 1963, 1966, 1973, 1977, 1979, 1982, 1983, 1987, 1993, 1994, 1997, 1999, 2003, 2011, 2017, 2018, 2019, 2026, 2027, 2029, 2031, 2038, 2039, 2041, 2042, 2049, 2053, 2059, 2062, 2063, 2066, 2069, 2073, 2078, 2081, 2083, 2087, 2089, 2098, 2099, 2102, 2103, 2111, 2113, 2122, 2123, 2126, 2127, 2129, 2131, 2137, 2138, 2141, 2143, 2147, 2153, 2157, 2161, 2167, 2173, 2174, 2179, 2181, 2182, 2186, 2189, 2194, 2199
Я, правда, поленился разбивать остальные 1760 чисел отрезка
![$[1..2200]$ $[1..2200]$](https://dxdy-01.korotkov.co.uk/f/8/4/6/8466df440af27cf42a664302ce385dd882.png)
на 4 группы по 440 чисел с произведениями
2504958280188081419921948972441396317993403801235686917189404793494410952319221107430699726426543482893150616818461328275525066728687821299944018804591123621764708436862923779082966701604255562735809
1289805092573842321119037749653748128030277852462704135079581240704766941274957290255116129389746051106781284949262988305500523148052986768314929608953462205114770269799533777220776888022882268969186
8256939455438775400312990802515143584992001317970206751063207265933958654529870772678667922698614937697266272985614883442793368986129518695143853094690122842913111643945798988875703895754483271038238
5182286564472391875215890301211571968504622359098107301057543005228410333158529079435309905796210654850747735976571461993013928271912292976427305555810117105923392750217796599906972251697366242580020
6575367017793348811892036002082886312661321854126266243791495009659816597145491149452188822078532158201083317945464571775879624578222350271609362065397049910467258829985447414830630497759605272939234
1842004607084907601089731497294700874743226451167075020005453698345376641104337205715485217753202924728864257010129270319864299599985377280000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000000000000000000.
Но, учитывая, что произведение этих чисел в точности равно 4-й степени вышеприведенного числа, я уверен, что это возможно.
Что касается второй гипотезы, полагаю, что для

подходит

. Среди

, меньших

требуемое разбиение возможно для

. Я не искал требуемого разбиения для большинства этих

, ограничившись составлением 4-й группы, для которой произведение остальных чисел является точным кубом.
Моя уверенность в том, что

базируется на том, что бОльших чисел 4-я группа составляется со все возрастающим запасом (из отрезка
![$[1..4n]$ $[1..4n]$](https://dxdy-02.korotkov.co.uk/f/d/1/5/d15be36ddb79bf5b56cf5df0ffb2788082.png)
можно изъять существенно меньше

чисел так, что произведение остальных будет кубом). Но точного доказательства у меня нет.
НаградыЗа решение задачи ММ236 участники Марафона получают следующие призовые баллы:
Анатолий Казмерчук - 9;
Виктор Филимоненков - 7;
Валентина Колыбасова - 7;
Владислав Франк - 7;
Евгений Гужавин - 7;
Владимир Дорофеев - 7;
Юрий Варламов - 7;
Дмитрий Курашкин - 6;
Владимир Чубанов - 6;
Константин Шамсутдинов -3.
Эстетическая оценка задачи - 4.6 балла