ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФЕРМА
Будем натуральные числа, которые удовлетворяют уравнению (1),
называть корнями уравнения Ферма и обозначать

,

,

и


.
Если искать решения уравнения (1) во множестве целых чисел,
то уравнение (1) является диофантовым уравнением Ферма,
решениями которого будут натуральными числа

,

,

и

.
Рассмотрим вещественное уравнение с вещественными переменными

,
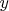
,

и


,
где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
.
Очевидно, что при

корни уравнения Ферма обращают функцию (2) в ноль, то есть
корни уравнения Ферма являются и корнями уравнения (2).
Следует заметить, что других корней уравнение (2) не имеет, то есть множества корней
уравнения Ферма и уравнения (2) совпадают, то есть уравнение (2) и уравнение Ферма эквивалентны.
Рассмотрим вещественную функцию вещественных переменных

,

,

и

(левая часть уравнения (2)).

где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
;

; a

и

- достаточно малое число.
Очевидно, что при

корни уравнения Ферма обращают функцию (2) в ноль,
то есть в этих точках функция (2) имеет локальные минимумы.
Таким образом, задачу решения диофантового уравнения Ферма (1) свели
к решению тригонометрического уравнения (2) и задаче нахождения экстремумов функции (3)
при

.
Запишем необходимые условия существования экстремума функции (3):


Будем искать координаты минимума функции (3) во множестве
натуральных координат, поэтому запишем необходимые условия существования экстремума
функции (3) в точках с целыми координатами

и

для чего координаты

и

подставим в уравнения (4) и (5).
Тогда получим


где
![$ z_0 = \sqrt[n]{x_0^n+y_0^n} $ $ z_0 = \sqrt[n]{x_0^n+y_0^n} $](https://dxdy-04.korotkov.co.uk/f/3/2/d/32d29d1dae4fd8f60ce788700d631aeb82.png)
.
Таким образом, получили два уравнения (6) и (7) с переменными

и

и
постоянными коэффициентами

и

.
В эти уравнения входит неопределенное число
![$\ z_0 = \sqrt[n]{(x_0^n+y_0^n)}$ $\ z_0 = \sqrt[n]{(x_0^n+y_0^n)}$](https://dxdy-04.korotkov.co.uk/f/f/c/5/fc5827990c1ee0af01be50743c2b896d82.png)
неопределенное в смысле того, что неизвестно какое значение оно принимает
целое или иррациональное. Чтобы исключить это число
преобразуем уравнения (6) и (7). Обе части уравнения (6) поделим на

, а
обе части уравнения (7) поделим на

, затем из первого полученного уравнения
вычтем второе полученное уравнение, тогда получим уравнение (8)

.
Любое уравнение вида

можно считать заданием неявной функции

.
Поэтому уравнение (8) можно рассматривать как неявную функцию
переменной

от переменной

, то есть

.
Таким образом, уравнение (8) позволяет найти при

функцию

, в которой

и

постоянны и не зависят от переменной

.
Из уравнения (8) я можно выразить зависимость

в явном виде:

График функции (9) показан на рис. 1.

Функция (9) определена при

, а в точке

функция (9) не определена.
Найдем по правилу Лопиталя предел функции (9) когда

.
Этот предел равен

.
Предел функции (9)

не зависиn от значений

и
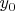
и равен 2,
то есть

при любых значениях

и
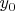
.
Мы нашли предел функции (9)

только и всего.
Функция (9) при

не позволяет определить координату экстремума функции (3),
чтобы определить эту координату надо вернуться к эквивалентному диофантовому уравнению Ферма.
Если есть решение диофантового уравнения Ферма, то координаты точки экстремума при

будут равны

,

,

и

.
На Рис. 1. точка

соответствует точке

, точке

соответствует выколотая точка

.
Следует заметить, что если

, то функция координат точек экстремумов будет иметь разрыв,
а если

, то функция координат точек экстремумов будет непрерывной.
Если функция координат точек экстремумов имеет разрыв в точке

, то это свидетельствует о том,
что не существует решений диофантового уравнения Ферма при

,
а если функция координат точек экстремумов непрерывна, то это свидетельствует о том,
что при данном

решения диофантового уравнения Ферма существуют.
Поскольку функция координат точек экстремумов при

и

имеет разрывы,
поэтому при

диофантовое уравнение Ферма не имеет решение.
Функция координат точек экстремумов только при

будет непрерывной, поэтому
диофантовое уравнение Ферма имеет решения только при

.
Графики функции при фиксированных х0 , у0 и n=3 показаны на Рис. 2.

Таким образом, теорема Ферма доказана.
Следует заметить, что доказательство теоремы Ферма выполнено методом, основанном
на сведении решения диофантового уравнения Ферма к решению
эквивалентного тригонометрического уравнения и нахождению минимумов функции,
получаемой из тригонометрического уравнения.
-- 26.11.2017, 18:58 --Коровьев !
У Вас уравнение

,
соответствующее функции (2) не эквивалентно уравнению (1).
-- 26.11.2017, 18:59 --Коровьев !
У Вас уравнение

,
соответствующее функции (2) не эквивалентно уравнению (1).