Здравствуйте! Растолкуйте, пожалуйста, одно место в книге. Определение последовательности:
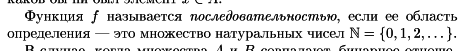
нигде не сказано, что функция

не может быть, к примеру, константой (для простоты речи ограничимся пока этим случаем). Ладно, хорошо. Идем дальше. Определение счетного множества (немного непривычное):

Т.е., ввиду сделанного выше замечания, бесконечное счетное множество может состоять из одного элемента (замечание №2).
Определение эквивалентных множеств:
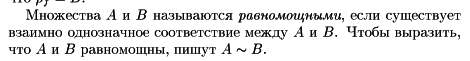
Теперь, собственно, вызвавшее затруднение доказательство:

Т.е. я

выбираю отличными от уже выбранных

. Ну как я могу это сделать для любого натурального

, если

может быть бесконечной последовательностью своего элемента? Там, заменив предположение

предположением, что бесконечное множество значении

состоит из элементов конечного множества, только записанных бесконечной последовательностью в каком-либо порядке, получу не менее интересный вопрос.
(Оффтоп)
Другое доказательство этого утверждения знакомо, интересно разобраться с этим.



