У меня мысль такая.
"Символ" - это не формальный термин, а "такая закорючка на бумаге / на доске, которой мы будем это обозначать". На это слово можно наплевать.
Содержательно, речь идёт о том, что имеется числовая бесконечная последовательность

и ей ставится в соответствие другая числовая последовательность
 частичных сумм
частичных сумм. Понятно, что называть рядом просто последовательность

нелепо. В теории рядов интересна взаимосвязь свойств

и

Значит, рядом назовём такую пару, исходная последовательность и её образ по этому отображению.
По сути, можно придумать много разных отображений последовательностей в последовательности. Возьмём одно из них, и обозначим

По сути, не важно, как мы его обозначим: в дальнейшей теории это просто некоторое константное отображение. Это не более сложная вещь, чем числовая константа
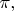
или функция

или множество

Очевидно, удобно вместо пары

указывать только один из элементов, а второй получать из первого, дописывая значок

Можно ввести другие такие значки:
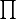
для частичных произведений,

или

И даже заметить симметрию: можно пользоваться

а можно

Просто первое используется по традиции.
-- 22.06.2017 01:59:28 --Глянул немного исходную тему. Там был вопрос: что означает
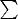
по множеству? Это уже, конечно, не ряд. Но можно взять множество подмножеств исходного множества, и даже сильнее, множество конечных подмножеств. И ему сопоставить множество частичных сумм. И исследовать свойства этого образа и отображения.



