Доказательство непрерывности функции

[NEvOl]

Здравствуйте, пытаюсь разобраться, в книге написано: Функция $y=f(x)$ называется непрерывной в точке $x_0$, если в этой точке имеет место быть следующее соотношение:
$$\lim_{\Delta x \to 0} \Delta y = \lim_{\Delta x \to 0}\left( f(x_0 + \Delta x) - f(x_0) \right) = 0$
Можем ли мы сделать так что бы доказать что функция непрерывна во всей области определения ?
$f(x)=cosec(x)$
$y+\Delta y = cosec(x+\Delta x)$
$\Delta y = cosec(x+\Delta x)-cosec(x)$

$$\lim_{\Delta x \to 0} cosec(x+\Delta x)-cosec(x)=cosec(x+0)-cosec(x)=0$
где значения $x$ принадлежат области определения функции $f(x)=cosec(x)$

[Aritaborian]

Нет, не можем. Написанное вами вообще ни малейшего смысла не имеет. А косеканс пишите так: $\cosec$.

[svv]

Нет, так нельзя. Вас должно было смутить, что применяемая магия:

NEvOl в сообщении #1140673 писал(а):

$\lim_{\Delta x \to 0} cosec(x+\Delta x)-cosec(x)=cosec(x+0)-cosec(x)=0$

позволяет сделать вывод о непрерывности функции, ничего о ней не зная.

[NEvOl]

svv в сообщении #1140676 писал(а):

Вас должно было смутить

Так оно и было, по-этому я решил спросить у знающих людей, ибо обосновать сам не могу почему так делать нельзя(
В книге $$\Delta y$ преобразовывается до вида:

$$\Delta y = \frac{2\cos(x+\frac{\Delta x}{2})\sin(-\frac{\Delta x}{2})}{\sin(x+\Delta x)\sin(x)}$$

В итоге

$$\lim_{\Delta x \to 0} \frac{2\cos(x+\frac{\Delta x}{2})\sin(-\frac{\Delta x}{2})}{\sin(x+\Delta x)\sin(x)} =\frac{2\cos(x)}{(\sin(x))^2}0=0 $$

Но не совсем понимаю для чего это сделано, подскажите пожалуйста. Разница в том что тут предел стремиться к бесконечно малой величине а в предыдущем примере он равен 0 ?

[AV_77]

Разница в том, что вы по какой-то причине заменяете $\Delta x$ на его предельное значение $0$ никак это не обосновывая.

[Aritaborian]

NEvOl, а вот давайте вы сейчас возьмёте учебник матана и заново выучите понятия предела и бесконечно малой величины. Вы же постыдно плаваете в самых что ни на есть основах.

[Mihr]

NEvOl в сообщении #1140678 писал(а):

Но не совсем понимаю для чего это сделано, подскажите пожалуйста.

Для того, чтобы воспользоваться непрерывностью синуса и косинуса, которая наверняка была доказана ранее.

[Aritaborian]

Господа, зачем вы помогаете этому неучу? Ну что это за слова такие?

NEvOl в сообщении #1140678 писал(а):

предел стремиться к бесконечно малой величине а в предыдущем примере он равен 0 ?

Вас это не настораживает? Безграмотность на безграмотности едет и безграмотностью погоняет, тьфу! Да любой университетский препод, узрев такое, снял бы очки, достал носовой платок и погнал бы им этого нерадивого тунеядца прочь. А вы пресловутым носовым платком ему сопли вытираете.

[Mikhail_K]

NEvOl в сообщении #1140673 писал(а):

$$\lim_{\Delta x \to 0} cosec(x+\Delta x)-cosec(x)=cosec(x+0)-cosec(x)=0$$

Вот здесь ошибка. Всё дело в том, что вот так вот "подставить" $\Delta x=0$ внутрь предела:

$$ \lim\limits_{\Delta x\to 0}{\rm{cosec}}(x+\Delta x)={\rm{cosec}}(x+0)={\rm{cosec}}x $$

- можно, но только если непрерывность функции ${\rm{cosec}}$ уже известна. Вам же она неизвестна, Вам эту непрерывность надо доказать.
Вообще, подобные "подстановки" типа $\lim\limits_{x\to x_0}f(x)=f(x_0)$ часто приходится делать, но делать их можно только тогда, когда про функцию $f$ уже точно известно, что она непрерывна.

(Оффтоп)

Aritaborian в сообщении #1140684 писал(а):

Господа, зачем вы помогаете этому неучу? Безграмотность на безграмотности едет и безграмотностью погоняет, тьфу!

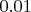
Да, едет и погоняет. Но мне вот по долгу службы приходится иметь дело и с гораздо более тяжёлыми случаями. Не так давно выясняли со студенткой-математиком 4 курса (практически выпускницей), чему равен предел $1/x$ при $x\to 0$. Попутно выяснилось, что она совсем не представляет, какие точки ближе к нулю, а какие дальше на числовой прямой, и не способна разделить $1$ на $0.1$ или на $0.01$ без калькулятора. И это не единичный случай. Тем не менее, в любом, даже самом тяжёлом случае есть возможность студенту хоть что-то прояснить, и он станет понимать то, чего не понимал ранее. Я для себя решил, что если есть хотя бы мизерный педагогический результат, то я не зря тратил свою энергию на разъяснения.

[Otta]

(Оффтоп)

Mikhail_K в сообщении #1140692 писал(а):

Тем не менее, в любом, даже самом тяжёлом случае есть возможность студенту хоть что-то прояснить, и он станет понимать то, чего не понимал ранее.

В подавляющем большинстве случаев, - чтобы через пять минут об этом благополучно забыть. :(

[Aritaborian]

(Оффтоп)

Ну и кто был прав? Пришёл университетский препод и всех разогнал.

[NEvOl]

Mikhail_K в сообщении #1140692 писал(а):

Вообще, подобные "подстановки" типа $\lim\limits_{x\to x_0}f(x)=f(x_0)$ часто приходится делать, но делать их можно только тогда, когда про функцию $f$ уже точно известно, что она непрерывна.

т.е. я правильно понял что, что бы доказать что функция непрерывна в точке $x_0$ нужно показать следующее:

$$\lim_{\Delta x \to 0} \Delta y=0$$

но при этом преобразовав $\Delta y$ до функций непрерывность которых уже доказана и затем находить предел ?
Еще одно уточнение, я так понимаю что

$$\lim\limits_{x\to x_0}f(x)=f(x_0) (1)$$

только тогда, когда $f$ непрерывна в точке $x_0$, но я "натыкался" на упоминания о том что $\lim\limits_{x\to x_0}f(x)=f(x_0)$ когда $x_0$ принадлежит области допустимых значений функции $f$, но т.к. функция $f$ непрерывна в точке $x_0$ следовательно $x_0$ точно принадлежит области допустимых значений и ограничение $(1)$ строже, следовательно нужно придерживать его $(1)$ ?

[Otta]

NEvOl в сообщении #1140765 писал(а):

т.е. я правильно понял что, что бы доказать что функция непрерывна в точке $x_0$ нужно показать следующее:

$$\lim_{\Delta x \to 0} \Delta y=0$$

но при этом преобразовав $\Delta y$ до функций непрерывность которых уже доказана и затем находить предел ?

Например, так, да.

NEvOl в сообщении #1140765 писал(а):

я "натыкался" на упоминания о том что $\lim\limits_{x\to x_0}f(x)=f(x_0)$ когда $x_0$ принадлежит области допустимых значений функции $f$, но т.к. функция $f$ непрерывна в точке $x_0$ следовательно $x_0$ точно принадлежит области допустимых значений и ограничение $(1)$ строже, следовательно нужно придерживать его $(1)$ ?

Набор слов. Процитируйте, пожалуйста, дословно, на что Вы натыкались.

[Aritaborian]

И где именно.

[NEvOl]

Формулировка примерно следующая: $f(x)$ - элементарная функция, точка $a$ лежит в области определения этой функции, тогда

$$\lim_{x \to a} f(x) = f(a)$$

.