Растут ли чёрные дыры?

[Degen1103]

Degen1103 в сообщении #1116818 писал(а):

Ещё вопрос: о луковичной структуре. Возьмём большую ЧД сравнительно невысокой плотности. Может ли внутри неё свой коллапс произойти, чтоб горизонт под горизонтом образовался?... И т.д.?...

А, оказывается, уже обсуждали, в январе прошлого года. Выходит, не такую уж глупость ляпнул

[kortes74]

Внешний наблюдатель увидит что его друг застыл навечно у горизонта событий для внутреннего наблюдателя начнуть краснеть и гаснуть звезды пока не наступит абсолютная тьма остановки времени

[Munin]

Это неправда, и много раз было говорено.

[Pphantom]

Тема перемещена из форума «Астрономия» в форум «Помогите решить / разобраться (Ф)»
Причина переноса: поехали-ка сюда, к астрономии это все имеет весьма смутное отношение.

[specialist]

Munin в сообщении #1090243 писал(а):

irygaev в сообщении #1090190 писал(а):

Спасибо. Какая подготовка требуется для чтения этой книги?

Для чтения этой книги - достаточно СТО и электродинамики. Остальное излагается в самой книге. Хотя и в предыдущих главах, а не непосредственно в главе про чёрную дыру.

Товарищ Munin с высот своих знаний, и специфики образования, выразился довольно формально. МТУ - книга очень хорошая, но чтоб начать её понимать (не ОТО, а именно МТУ), необходимо помимо СТО и электродинамики, курс линейной алгебры и функций многих переменных обязательно с дифформами (допустим в нашем вузе, когда читали курс линейной алгебры, линейные формы опустили, а про дифформы мы вообще не слышали) основы тензорного исчисления (авторы с самого начала используют индексные обозначения, но при этом еще говоря о тензорах как о "машинах", но операции на тензорах будут даны только на 112 странице), основы дифференциальной геометрии (чтоб иметь представление как понимают другие авторы). Желательно набрать как можно больше разных книжек по этим областям и книга поддастся. Да и это только для первого тома МТУ.
P.S это мое личное, субъективное мнение инженера, основанное на опыте с этой книгой, возможно вам действительно хватит электродинамики и СТО.

[Munin]

specialist в сообщении #1126985 писал(а):

необходимо... курс линейной алгебры и функций многих переменных обязательно с дифформами... основы тензорного исчисления... основы дифференциальной геометрии.

Во-первых, я просто не упоминал математики. Только подготовку по физике.

Во-вторых, необходимы только линейная алгебра (с тензорами) и функции многих переменных. Дифформы и дифгеометрия рассказываются в самой книге МТУ.

Конечно, желательно читать другие книжки. Но увы, довольно многие (не самые лучшие) книжки излагают эти вопросы хуже, чем МТУ. Тут надо быть довольно придирчивым.

[Pphantom]

Рассуждения об аналогиях и фактологии отделены в «Листы и прочий оффтопик»

[irygaev]

Кажется у меня сложилась в голове картинка по исходному вопросу, но хотелось бы понять, правильная ли.

Смущает вот это заявление:

Munin в сообщении #1090179 писал(а):

Он будет выглядеть бесконечным. "Быть для наблюдателя" - оксюморон.

Но ведь это два разных понятия и два разных момента времени - 1) когда событие произошло по часам удалённого наблюдателя и 2) когда информация о нём дошла до него. Первое я называл быть, второе - выглядеть, возможно, неправильно.

Как я теперь понимаю, на горизонте событий световой конус падающего наблюдателя наклоняется так, что его край оказывается направлен "вверх", параллельно мировой линии удалённого наблюдателя, поэтому они никогда не пересекутся, т.е. свет и информация до удалённого наблюдателя не дойдёт. Но это же не значит, что само падение заняло бесконечное время по часам удалённого наблюдателя, верно? Оно заняло конечное время, хоть и большее, чем у падающего. То есть время на горизонте событий замедляется не до нуля, правильно?

Вот картинка. Пока у падающего наблюдателя прошёл отрезок времени CD, у удалённого — AB. AB длиннее CD, но не бесконечно длинный. А бесконечно длинным станет отрезок AE, если фотон летит непосредственно из точки D на горизонте событий.

[Munin]

irygaev в сообщении #1132196 писал(а):

Но ведь это два разных понятия и два разных момента времени - 1) когда событие произошло по часам удалённого наблюдателя и 2) когда информация о нём дошла до него. Первое я называл быть, второе - выглядеть, возможно, неправильно.

Дело в том, что "1" вообще не определено. Можно вводить разные системы координат, в которых "событие по часам удалённого наблюдателя" будет происходить в разные моменты времени. Причём с разбросом от $0$ до $+\infty,$ так что это вопрос не праздный.

irygaev в сообщении #1132196 писал(а):

Как я теперь понимаю, на горизонте событий световой конус падающего наблюдателя наклоняется

Это в координатах Эддингтона-Финкельштейна. Они очень удобны для рассмотрения падающего наблюдателя.

Но есть и ещё много других систем координат. Наиболее часто упоминаются:
Шварцшильда - в них "падения через горизонт" вообще не происходит в конечный момент времени;
Крускала / Крускала-Секереша (вторую фамилию как только ни транскрибируют) - удобна для рассмотрения глобальных вопросов.
И не только эти. Например, в Ландау-Лифшице упоминается система координат Леметра.

irygaev в сообщении #1132196 писал(а):

Но это же не значит, что само падение заняло бесконечное время по часам удалённого наблюдателя, верно?

Да. Для выдуманной величины "время по часам удалённого наблюдателя" это вообще ничего не значит. В одних координатах это "время" будет одним, в других - другим, в третьих - третьим.

irygaev в сообщении #1132196 писал(а):

То есть время на горизонте событий замедляется не до нуля, правильно?

Да (для падающего через горизонт наблюдателя), но не "то есть", а по другим причинам. В промежутке вы написали то, что неверно (верно только в координатах Эддингтона-Финкельштейна).

irygaev в сообщении #1132196 писал(а):

Вот картинка.

Эта картинка называется "координаты Эддингтона-Финкельштейна".

[irygaev]

Munin в сообщении #1132203 писал(а):

Дело в том, что "1" вообще не определено. Можно вводить разные системы координат, в которых "событие по часам удалённого наблюдателя" будет происходить в разные моменты времени.

Я подозревал подобное.

А если мы возьмём плоское пространство Минковского (т.е. только СТО, и только ИСО в ней), 1 будет определено? Или опять возможны различные системы координат?
Вот на этом рисунке, можно ли говорить, что событие B произошло в момент A по часам покоящегося наблюдателя?

Munin в сообщении #1132203 писал(а):

irygaev в сообщении #1132196 писал(а):

Как я теперь понимаю, на горизонте событий световой конус падающего наблюдателя наклоняется

Это в координатах Эддингтона-Финкельштейна.

Разве сам факт наклона световых конусов в разных точках относительно друг друга при искривлении пространства-времени зависит от системы координат?

Munin в сообщении #1132203 писал(а):

Для выдуманной величины "время по часам удалённого наблюдателя" это вообще ничего не значит. В одних координатах это "время" будет одним, в других - другим, в третьих - третьим.

Верно ли, что, задав систему координат, мы задаём способ синхронизации времени? Или эти вещи независимы?
Вот на моей первой картинке красные прямые - это "правильные" линии одновременности для удалённого наблюдателя в координатах Эддингтона-Финкельштейна? Или только одни из возможных? Или вообще неправильные?

[Geen]

irygaev в сообщении #1132381 писал(а):

по часам покоящегося наблюдателя?

"Покоящийся наблюдатель" - это большая условность.

irygaev в сообщении #1132381 писал(а):

Разве сам факт наклона световых конусов в разных точках относительно друг друга при искривлении пространства-времени зависит от системы координат?

А что такое "наклон относительно друг друга в разных точках"? Вот, например, в координатах Крускала конусы наклонены?

irygaev в сообщении #1132381 писал(а):

Верно ли, что, задав систему координат, мы задаём способ синхронизации времени? Или эти вещи независимы?

Координаты - это просто "произвольные" числа, которыми мы помечаем события. Они не имеют физического смысла. Например, координаты Эддингтона-Финкельштейна могут быть двух типов - когда прямыми "изображаются" падающие в центр световые лучи или когда прямые исходящие. Если переходить от одних к другим, то координаты событий изменяться, диаграмма "деформируется", но если решаемая задача физически таже самая, то ответ в ней не измениться.

irygaev в сообщении #1132381 писал(а):

Вот на моей первой картинке красные прямые - это "правильные" линии одновременности для удалённого наблюдателя в координатах Эддингтона-Финкельштейна? Или только одни из возможных? Или вообще неправильные?

Или вопрос плохой Ведь тут ещё бы понять зачем Вам эта "одновременность" понадобилась.

[irygaev]

Geen в сообщении #1132401 писал(а):

"Покоящийся наблюдатель" - это большая условность.

Вы просто ушли от ответа. Хорошо, я уточню. По часам наблюдателя, мировая линия которого на этом рисунке направлена строго вверх.

Geen в сообщении #1132401 писал(а):

Ведь тут ещё бы понять зачем Вам эта "одновременность" понадобилась.

Линии одновременности задают "мгновенное пространство" наблюдателя, мгновенный трёхмерный срез четырёхмерного пространства-времени. Хочу выяснить, есть ли вообще такое понятие как "мгновенное пространство". Пока получается, что в плоском пространстве Минковского (в СТО) вроде бы есть (или я просто привык так считать), а в искривлённом (в ОТО) - уже нет (точнее его нельзя задать однозначно). Правильно или нет?

[Munin]

irygaev в сообщении #1132381 писал(а):

А если мы возьмём плоское пространство Минковского (т.е. только СТО, и только ИСО в ней), 1 будет определено? Или опять возможны различные системы координат?
Вот на этом рисунке, можно ли говорить, что событие B произошло в момент A по часам покоящегося наблюдателя?

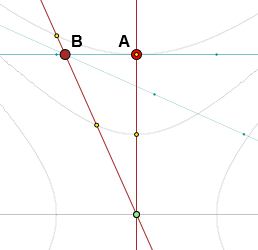
Можно, но надо понимать, что это условность. Эта условность принята в СТО, но от неё приходится отказываться в ОТО. Вот что вам надо уловить.

irygaev в сообщении #1132381 писал(а):

Разве сам факт наклона световых конусов в разных точках относительно друг друга при искривлении пространства-времени зависит от системы координат?

Ага. Например, в системе координат Шварцшильда вообще никакого наклона нет. И в системе координат Крускала-(Секереша).

Этот "наклон" нужен только для того, чтобы проиллюстрировать, как световые конусы расположены на горизонте. Причём, к ним надо подойти "гладко" снаружи, без резких рывков.

В системе координат Шварцшильда, сам горизонт не рассматривается, и "наклонять" конусы не нужно. В системе координат Крускала-(Секереша) горизонт не нарисован как вертикальная линия, поэтому и конусы можно не наклонять.

Вообще, вам надо привыкнуть, что все эти разные системы координат и способы изображения - в чём-то аналогичны разным картографическим проекциям сферической Земли на плоскость карты. Можно нарисовать карту с большой Гренландией и маленькой Индией. Можно нарисовать карту, где юг будет сверху или слева. От этого сама Гренландия не увеличится, а Москва не станет южней Лондона.

irygaev в сообщении #1132381 писал(а):

Верно ли, что, задав систему координат, мы задаём способ синхронизации времени?

По сути, да.

irygaev в сообщении #1132381 писал(а):

Вот на моей первой картинке красные прямые - это "правильные" линии одновременности для удалённого наблюдателя в координатах Эддингтона-Финкельштейна?

Правильные, в том смысле, что они соответствуют некоторым линиям $t=\mathrm{const}$ системы координат.

Но тут надо оговорить, что вообще вовсе не обязательно в системе координат должна быть вообще одна из координат со смыслом "времени". Ни глобально (какая-нибудь $t$ может быть где-то в роли времени, а где-то - нет), ни даже локально (можно ввести такие координаты $x_1,x_2,x_3,x_4,$ что ни одна из этих координат не сгодится на роль времени). Единственное, ради чего вводятся координаты с подобными буковками $t,$ - это наглядность, особенно для тех, кто не слишком глубоко проник в физику ОТО.

irygaev в сообщении #1132404 писал(а):

Линии одновременности задают "мгновенное пространство" наблюдателя, мгновенный трёхмерный срез четырёхмерного пространства-времени.

Вот только этот "мгновенный срез" целиком вымышленный и искусственный, и никакой особой роли не играет. Никакой реальной физики к нему не привязано.

irygaev в сообщении #1132404 писал(а):

Хочу выяснить, есть ли вообще такое понятие как "мгновенное пространство".

Есть - как мысленная конструкция!

Ровно так же, как на поверхности Земли есть параллели и меридианы, экватор - как вымышленные человеком линии. Их можно провести карандашом или выложить из камня. Но горы, реки и моря на эти линии не обращают никакого внимания, и звери в лесах об них не спотыкаются.

irygaev в сообщении #1132404 писал(а):

Пока получается, что в плоском пространстве Минковского (в СТО) вроде бы есть (или я просто привык так считать), а в искривлённом (в ОТО) - уже нет (точнее его нельзя задать однозначно). Правильно или нет?

Нет, и в плоском пространстве их нет. Просто в плоском пространстве удобней считать, что есть. Поэтому учебники СТО написаны с той точки зрения, что есть, а учебники ОТО - с той точки зрения, что нет.

[irygaev]

Munin в сообщении #1132408 писал(а):

Эта условность принята в СТО, но от неё приходится отказываться в ОТО. Вот что вам надо уловить.

Munin в сообщении #1132408 писал(а):

Нет, и в плоском пространстве их нет. Просто в плоском пространстве удобней считать, что есть. Поэтому учебники СТО написаны с той точки зрения, что есть, а учебники ОТО - с той точки зрения, что нет

Отлично, спасибо! Примерно такого ответа я и ждал.

Munin в сообщении #1132408 писал(а):

Вообще, вам надо привыкнуть, что все эти разные системы координат и способы изображения - в чём-то аналогичны разным картографическим проекциям сферической Земли на плоскость карты.

Да, понятно. Но такой вопрос ) Картинку в координатах Эддингтона-Финкельштейна можно продолжить влево от сингулярности? Там должно получиться симметрично. И в принципе можно нарисовать вторую чёрную дыру где-то справа, или вообще несколько дыр, если они расположены на одной прямой. Получится такой двумерный срез по одной пространственной координате. По-моему, это очень наглядно представило бы искривлённое пространство-время. Или так нарисовать нельзя? Или это будет некорректно?

[arseniiv]

Думаю, что стоит всё же добавить следующее. Чтобы понять, есть или нет «мгновенные пространства», надо попытаться сформулировать их определение. В СТО мы можем взять времениподобный вектор $u$ и какое-то событие $A$. Тогда можно сказать, что «мгновенное пространство» относительно $(A,u)$ состоит из событий $X$ таких, что $(X-A,u) = 0$ (тут скобки — это уже скалярное произведение, а не пара).

Теперь ОТО. Касательные пространства в каждом событии оказываются не тождественными, а ещё мы не можем больше сказать «$X-A$». Хотя мы всё ещё можем переносить векторы туда-сюда по геодезическим и другим кривым и выбирать геодезическую, проходящую через событие, по касательному к ней вектору. Как переформулируем?