Есть следующая исходная структурная схема:
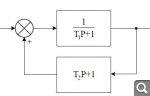
По правилам преобразования последовательно параллельных схем соединения (соединения с обратной связью) можно свернуть исходник и получить следующую передаточную функцию:

Известно, что

,

, подставив известные значения в полученную передаточную функцию, получим:

Этот блок можно смоделировать в матлабе.
Однако, можно использовать второй подход, и представить форсирующее звено в цепи обратной связи как сумму сигнала и производной от него, чтобы смоделировать её в матлабе. Обе схемы реализованы здесь:
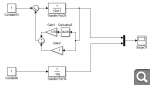
Но не могу разобраться, почему, казалось бы, одинаковые с точки зрения конечного результата схемы дают симметричные относительно оси

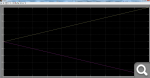
графики. Не пойму, мистика какая то, помогите пожалуйста разобраться. График на рисунке ниже: