Сонантометрия или алгебра музыкальной гармонии.

[Свободный Художник]

Свободный Художник в сообщении #1097997 писал(а):

Нам особенно важно то, что Пиаже сделал главной "фишкой" своего подхода свойство обратимости рассматриваемых операций:
"... Пиаже также открыл главное свойство этих операций - их обратимость. Характеризуя понятие обратимости, Пиаже привел в качестве примера арифметические действия - сложение и вычитание, умножение и деление..."

В свете генезиса муз. теории здесь можно было бы упомянуть еще и об операции взятия среднего пропорционального (как операции, обратной к операции взятия "двойного отношения" -- двукратного увеличения данного муз интервала):
http://www.px-pict.com/7/3/1/9/2/1/1/5.html
Декарт, кстати говоря, причислял операцию взятия среднего пропорционального к числу "основных" арифметических операций:
http://www.px-pict.com/9/6/5/1/2/1.html

-- Вт фев 09, 2016 23:49:08 --

Свободный Художник в сообщении #1091606 писал(а):

Вы же писали, что для Вас важна "основная теорема арифметики". Ее, однако, нельзя до конца понять без апелляции к аддитивным понятиям, как об этом написано, например, у Арнольда:
http://www.px-pict.com/7/4/1/2/7/13/103b.html
Учитывая, что в арифметике (положительных) рациональных чисел аддитивных понятий получается не одно, а два ($\bullet$ и $\circ$), причем абсолютно равноправных по отношению к мультипликативному понятию ($\cdot$), можно ожидать, что такая двойственность окажется каким-то образом полезной в контексте рассмотрений по "основной теореме арифметике". В принципе, эта идея реализована у Арнольда:
http://www.px-pict.com/7/4/1/2/7/13/104a.html

Как следует из чтения Арнольда, именно свойство обратимости дробей (в определенном смысле) лежит в основе интересующей нас двойственности:
http://www.px-pict.com/preprints/grundlagen/9.html
(пункт 3 на указаной странице)

[commator]

Свободный Художник в сообщении #1098237 писал(а):

В свете генезиса муз. теории здесь можно было бы упомянуть еще и об операции взятия среднего пропорционального (как операции, обратной к операции взятия "двойного отношения" -- двукратного увеличения данного муз интервала):

Имеется прототип такого упоминания:

Ноосфера писал(а):

Гармонический ряд есть арифметический ряд ($1\times\mathrm{f}, 2\times\mathrm{f}, 3\times\mathrm{f}, 4\times\mathrm{f}, 5\times\mathrm{f}, \dots$). В выражениях частоты (измеряется в циклах в секунду, или Герцах (Гц), где $\mathrm{f}$ основная частота), разница между последовательными гармониками есть поэтому постоянна и равна осноаной [частоте]. Но поскольку человеческие уши отзываются на звук нелинейно, высшие гармоники воспринимаются как "ближе друг к другу", чем нижние. С другой стороны, октавный ряд представляет собой геометрическую прогрессию ($2\times\mathrm{f}, 4\times\mathrm{f}, 8\times\mathrm{f}, 16\times\mathrm{f}, ...$), и люди слышат эти расстояния как "однообразность" в смысле музыкального интервала, В пределах того, что слышится, каждая октава в гармоническом ряду делится на всё более "мелкие" и более многочисленные интервалы..

(English)

The harmonic series is an arithmetic series ($1\times\mathrm{f}, 2\times\mathrm{f}, 3\times\mathrm{f}, 4\times\mathrm{f}, 5\times\mathrm{f}, ...$). In terms of frequency (measured in cycles per second, or hertz (Hz) where $\mathrm{f}$ is the fundamental frequency), the difference between consecutive harmonics is therefore constant and equal to the fundamental. But because human ears respond to sound nonlinearly, higher harmonics are perceived as "closer together" than lower ones. On the other hand, the octave series is a geometric progression ($2\times\mathrm{f}, 4\times\mathrm{f}, 8\times\mathrm{f}, 16\times\mathrm{f}, ...$), and people hear these distances as "the same" in the sense of musical interval. In terms of what one hears, each octave in the harmonic series is divided into increasingly "smaller" and more numerous intervals.

[Свободный Художник]

Алиса из Страны чудес:
https://ru.wikipedia.org/wiki/%D0%90%D0 ... 0%B5%D1%81
https://en.wikipedia.org/wiki/Alice%27s ... Wonderland
спрашивала:"Чему же вас учили?" И то, что ей отвечали:
http://www.px-pict.com/10/3/4/14/9/2.html
могло свидетельствовать о том, что нет особой ясности по поводу "основных" операций арифметики. Декарт считал, что их четыре или пять:

Свободный Художник в сообщении #1098237 писал(а):

Декарт, кстати говоря, причислял операцию взятия среднего пропорционального к числу "основных" арифметических операций:
http://www.px-pict.com/9/6/5/1/2/1.html

С другой стороны, почему бы не добавить к ним операции взятия НОД и НОК на множестве положительных рациональных чисел:
http://www.px-pict.com/preprints/grundlagen/9.html
(пункт 4 на указанной странице)
Эти операции важны для более полного выявления феномена двойственности в системе положительных рациональных чисел.

[commator]

Свободный Художник в сообщении #1099181 писал(а):

из Страны чудес:

Кто-то писал(а):

Принцип заключен не только в количестве чисел, а преимущественно в их качественном расположении

[Свободный Художник]

Свободный Художник в сообщении #1099181 писал(а):

С другой стороны, почему бы не добавить к ним операции взятия НОД и НОК на множестве положительных рациональных чисел:
http://www.px-pict.com/preprints/grundlagen/9.html
(пункт 4 на указанной странице)
Эти операции важны для более полного выявления феномена двойственности в системе положительных рациональных чисел.

Особенно важным для нас является следующее обстоятельство, отмеченное Арнольдом:
"Доказанная теорема позволяет притти независимо от теорем 1 и 2 параграфа 103 к доказательству основной теоремы о делимости произведения":
http://www.px-pict.com/7/4/1/2/7/13/105.html
(пункт 2 на указанной странице)

Свободный Художник в сообщении #1091606 писал(а):

Вы же писали, что для Вас важна "основная теорема арифметики". Ее, однако, нельзя до конца понять без апелляции к аддитивным понятиям, как об этом написано, например, у Арнольда:
http://www.px-pict.com/7/4/1/2/7/13/103b.html
Учитывая, что в арифметике (положительных) рациональных чисел аддитивных понятий получается не одно, а два ($\bullet$ и $\circ$), причем абсолютно равноправных по отношению к мультипликативному понятию ($\cdot$), можно ожидать, что такая двойственность окажется каким-то образом полезной в контексте рассмотрений по "основной теореме арифметики".

Свободный Художник в сообщении #1099181 писал(а):

Эти операции важны для более полного выявления феномена двойственности в системе положительных рациональных чисел.

О сответствующей дистрибутивной решетке я уже упоминал в теме о двойственности:

Свободный Художник в сообщении #225875 писал(а):

Дистрибутивная решетка на множестве натуральных чисел, порождаемая операциями НОД и НОК, естественным образом обобщается до соответствующей дистрибутивной решетки на множестве положительных рациональных чисел...
Значит, мы можем промоделировать эту дистрибутивную решетку внутри системы $\mathbf{Q^+}$:

Свободный Художник в сообщении #144753 писал(а):

Например, если определить систему: $\mathbf{Q^+} = \langle \, \mathrm{Q^+}, \bullet\,, \circ\,, \overline{\phantom{a}} \rangle$,
где $\mathrm{Q^+}$ есть множество положительных рациональных чисел;
$\bullet$ есть бинарная операция на множестве $\mathrm{Q^+}$, определяемая как $x \bullet y = x + y$;
$\circ$ есть бинарная операция на множестве $\mathrm{Q^+}$, определяемая как $x \circ y = \dfrac{xy}{x + y}$;
$\overline{\phantom{a}}$ есть унарная операция на множестве $\mathrm{Q^+}$, определяемая как $\overline{x} = \dfrac1{x}$;
то в системе $\mathbf{Q^+}$ будут справедливы многие законы, имеющие место быть в булевой алгебре, например, законы де Моргана: $\overline{x \bullet y} = \overline{x} \circ \overline{y}$ и $\overline{x \circ y} = \overline{x} \bullet \overline{y}$.

Если согласиться, что операцию умножения внутри системы $\mathbf{Q^+}$ мы все-таки определили...
Т. е. после этих доопределений $\mathbf{Q^+}$ становится решеточно-упорядоченной абелевой группой относительно операции умножения.

Дожали таки мы $\mathbf{Q^+}$ до дистрибутивной решетки.
Стало быть и теорема Стоуна о представлении здесь рулит.

-- Вс фев 14, 2016 20:47:10 --

Свободный Художник в сообщении #1090248 писал(а):

Доказательство того, что ко-сложение $\circ$ и умножение $\cdot$ связаны в $\overline R$ законом дистрибутивности:
$\left(\dfrac{x}{a} \cdot \dfrac{z}{c}\right) \circ \left(\dfrac{y}{b} \cdot \dfrac{z}{c}\right) = \dfrac{xz}{ac} \circ \dfrac{yz}{bc}$
$\dfrac{xz}{ac} \circ \dfrac{yz}{bc} = \dfrac{xyz^2}{xzbc + acyz}$
$\dfrac{xyz^2}{xzbc + acyz} = \dfrac{xyz}{xbc + acy}$
$\dfrac{xyz}{xbc + acy} = \left(\dfrac{xy}{ay + bx}\right) \cdot \dfrac{z}{c}$
$\left(\dfrac{xy}{ay + bx}\right) \cdot \dfrac{z}{c} = \left(\dfrac{x}{a} \circ \dfrac{y}{b}\right) \cdot \dfrac{z}{c}$
Просто хладнокровно записываем последовательность соответствующих "переписывающих соотношений", как к тому призывает Стюарт:
http://www.px-pict.com/9/6/6/6/6.html

По поводу общих переписывающих систем (Term Rewriting Systems), конструкции которых планируется применять дальше, см.:
https://en.wikipedia.org/wiki/Rewriting
http://mathworld.wolfram.com/TermRewritingSystem.html
http://www.px-pict.com/9/6/2/2/1.html

[Свободный Художник]

Свободный Художник в сообщении #1092687 писал(а):

Однако с целью наибольшего удобства рассуждений о "гармоническом дуализме" я решил не жадничать и дать на звуко-высотность и интервало-широтность не одну, а две взаимно-ортогональные оси. О чем честно и сообщил во вводном параграфе:
http://www.px-pict.com/9/6/8/2/1/1/2/1.html
Значит, всего осей будет три. Временно абстрагируясь от временнОй оси, получаем две оси, одна из которых (на время этого абстрагирования) будет условно считаться горизонтальной, а другая -- вертикальной.

Содержательную интерпретацию используемых упорядоченных пар (в общем случае, положительных вещественых) чисел можно уточнить с помощью рисунков, приведенных в книге Д. Ф. Егорова:
http://www.px-pict.com/7/4/1/2/17/3.html
(Фиг. 2 и Фиг. 3 на указанной странице)
Содержательно такие упорядоченные пары будут интерпретироваться как "упорядоченные пары длин струн".
Сразу после Фиг. 2 Д. Ф. Егоров пишет: "Прямые $x = a$, $y = b$ вместе с осями ограничивают некоторый прямоугольник". Длина стороны этого прямоугольника, параллельной оси абсцисс, будет интерпретироваться как первый элемент упорядоченной пары "длин струн" (а сама сторона будет интерпретироваться как "первая струна упорядоченной пары струн"), тогда как длина стороны этого прямоугольника, параллельная оси ординат, будет интерпретироваться как второй элемент упорядоченной пары "длин струн" (а сама сторона будет интерпретироваться как "вторая струна упорядоченной пары струн").

[commator]

Свободный Художник в сообщении #1098237 писал(а):

Как следует из чтения Арнольда, именно свойство обратимости дробей (в определенном смысле) лежит в основе интересующей нас двойственности: http://www.px-pict.com/preprints/grundlagen/9.html
(пункт 3 на указаной странице)

Сегодня попалось на глаза:

Математик в Сети писал(а):

пишут Холопов - Поспелова, что никто до Царлино не обучал теории музыки с до, а обучали именно с ре.
Так зачем же Царлино все перековеркал? Просто "моча в голову ударила"? Или есть все же какая-то более существенная причина?

Посмотришь на рисунок с (отрезком) квинтовой спирали:
http://www.px-pict.com/7/3/2/5/1.html

и ясно видишь, что ре ― по центру, а фа и си (среди основных звуков) ― по краям.
А до и не в центре, и не с краю.

Так какая есть причина для переписывания ладов именно с до?

Математик в Сети писал(а):

Попозже изложу свою версию.

Была ли упомянутая версия изложена?

[Свободный Художник]

Нет, не была. Хотелось дополнительно разобраться с некоторыми нюансами. Теперь, в принципе, это возможно: у Olorulus'a в библиотеке выложены нужные работы:
Harold Powers. Mode / The New Grove Dictionary of Music and Musicians (1980) (PDF, 15 Mb)
Harold Powers. Mode / The New Grove Dictionary of Music and Musicians (2001) (PDF, 3 Mb)
http://www.kholopov.ru/dl_rus.html
(в конце указанной страницы)

[commator]

Если дело в ладах, Вы полагаете, то надо заглянуть ещё в одну книжицу:

bntr в сообщении #1061064 писал(а):

Теория многоосновности ладов и созвучий ч.II Гарбузова.

-- 27.02.2016, 23:50 --

Картинка Царлино заставляет думать, что всё у него начинается с A (т. е. ля), по алфавиту.

commator в сообщении #1031148 писал(а):

bntr в сообщении #1031098 писал(а):

Интересно, что получается a-moll

Первичность $a\mathsf{-}moll$ нагляднейшим образом демонстрирует картинка основателя теории чистого строя:

Zarlino 1558 писал(а):

Белым клавишам большой октавы его инструмента присвоены большие буквы

A, H*, C, D, E, F, G;

на клавишах малой октавы и выше — малые буквы

a, h*, c, d, e, f, g.

Нынешняя система буквенных имён поддерживает первичность $C\mathsf{-}dur$; в ней Царлино пришлось бы нанести на клавиши такие буквы:

A, H, c, d, e, f, g, a, h, c1, d1, e1, f1, g1, a1,

что смотрится гораздо менее убедительным поводом для размещения клавиш класса А в начале, середине и конце клавиатуры его инструмента.

*) h, особенно готическое $\mathfrak{h}$ похоже на b-квадратное, по-французски becarre, т. е. бекар и международный значок , первоначально обозначавший твёрдую, жёсткую b, в отличие от обычной, округлой и мягкой $\mathfrak{b}$, по-французски bemol, у нас имя бемоль для международного значка . Произносить имя ноты H, h как аш, эйч или ха, как у наc повелось, не вполне правильно. Лучше бекар, что и написано на соотаетсвующих клавишах Царлино.

commator в сообщении #997469 писал(а):

В сонантометрических преобразованиях удобно избавиться от $H$ и вместо $B, H, His$ писать не $B$♭, $B$♮, $B$♯, а $Bes, B, Bis$, что на нотном стане будет отображаться некоторыми подмножествами высотных классов Си-бемоль, Си-бекар и Си-диез.

[Свободный Художник]

commator в сообщении #1101718 писал(а):

Сегодня попалось на глаза:

Математик в Сети писал(а):

пишут Холопов - Поспелова, что никто до Царлино не обучал теории музыки с до, а обучали именно с ре.
Так зачем же Царлино все перековеркал? Просто "моча в голову ударила"? Или есть все же какая-то более существенная причина?

Посмотришь на рисунок с (отрезком) квинтовой спирали:
http://www.px-pict.com/7/3/2/5/1.html

и ясно видишь, что ре ― по центру, а фа и си (среди основных звуков) ― по краям.
А до и не в центре, и не с краю.

Так какая есть причина для переписывания ладов именно с до?

Честно говоря, для меня интерес к упомянутому Вами вопросу начался с рисунков из книги Ю. Н. Холопова:
http://www.px-pict.com/7/3/2/5/14/8/5.html
и с приведенного там замечания о связях этой концепции с построениями Оголевца. С размышлениями последнего о дорийском ладе можно ознакомиться здесь:
http://www.px-pict.com/7/3/2/4/10/5.html

-- Вс фев 28, 2016 23:50:27 --

Интересно, что Modern Dorian Mode иногда называют "русским минором":
https://en.wikipedia.org/wiki/Dorian_mode

[commator]

Свободный Художник в сообщении #1102945 писал(а):

для меня интерес к упомянутому Вами вопросу начался с рисунков из книги Ю. Н. Холопова: http://www.px-pict.com/7/3/2/5/14/8/5.html

Свободный Художник в сообщении #1102945 писал(а):

Интересно, что Modern Dorian Mode иногда называют "русским минором": https://en.wikipedia.org/wiki/Dorian_mode

Как бы он индийским не оказался, если его не греки или арии в Индию занесли:

Datta & Others 2006 писал(а):

Хотя древние трактаты не раскрывают ничего о действительном размере суар, некоторые интервальные соотношения могут быть построены с помощью подсказок в Натьяшастре. Например Бхарата говорил о консонантных интервалах девяти и тринадцати шрути. Мы знаем, что наиболее консонантные интервалы 4/3 и 3/2. Рассмотрим 4/3 как девять-шрути интервал и 3/2 как тринадцать-шрути интервалы. Отмечая распределение шрути 3, 2, 4, 4, 3, 2 и 4 для суар Sa, Ri, Ga, Ma, Pa, Dha и Ni соответственно некоторые разумные соотношения интервалов могут быть получены для всех нот, кроме Ri и Dha (рис1). Дадим, Ma и Pa быть 4/3 и 3/2 соответственно. Тогда, как Ni есть девять-шрути интервал от Ma его соотношение будет 16/9. Тогда Ga будет половина 16/9 х 4/3, т.е. 32/27. Очевидно также, что четыре-шрути интервал составит 3/2 ÷ 4/3 = 9/8. Ri будучи только 3 шрути вверх от Sa мы имеем предположить подходящим консонантным соотношением менее чем 9/8 для три-шрути интервала. 10/9 есть такое соотношение, что есть около 22 центов ниже 9/8. Если мы возьмем Ri быть 10/9, то Dha становится 10/9 х 3/2 = 5/3.

(English)

Though the ancient treatises do not reveal anything about the objective measure of swaras, some interval ratios can be built up using the hints in Nātyashāstra. For example Bharata has talked about consonant intervals of nine and thirteen shrutis. We know that most consonant intervals are 4/3 and 3/2. Let us consider 4/3 as a nine-shruti interval and 3/2 as the thirteen-shruti intervals. Noting the shruti distribution 3, 2, 4, 4, 3, 2 and 4 for swaras Sa, Ri, Ga, Ma, Pa, Dha and Ni respectively some reasonable ratio intervals may be derived for all notes except Ri and Dha (fig1). Let us assume Ma and Pa to be 4/3 and 3/2 respectively. Then as Ni is nine-shruti interval from Ma its ratio would be 16/9. Then Ga would be half of 16/9 x 4/3 i.e., 32/27. It is also obvious that a four-shruti interval would be 3/2 ÷ 4/3 = 9/8. Ri being only 3 shruti up from Sa we have to assume a suitable consonant ratio less than 9/8 for a three-shruti interval. 10/9 is such a ratio, which is about 22 cents below 9/8. If we take Ri to be 10/9 then Dha becomes 10/9 x 3/2 = 5/3.

[commator]

commator в сообщении #1103314 писал(а):

Как бы он индийским не оказался, если его не греки или арии в Индию занесли:

Уместно вспомнить:

commator в Сети писал(а):

Математик в Сети писал(а):

Точнее, я здесь вот что хотел сказать.

В “чистом строе” каждый звук обрастает вокруг себя акустическими значениями бемольных и диезных изменений таким образом, что “качественно нормированные” зоны остаются как бы ячейками, строго отделенными друг от друга.

А вот в пифагорейском строе имеет место быть принципиально иная картина:
http://www.px-pict.com/7/3/2/4/4/1.html

О В. Ф. Одоевском на стр. 24 журнала Старинная музыка №№3-4, 2005.
<<…
в 1860-е го­ды Владимир Федорович напряженно работал, пытаясь осмыслить закономерности русской народной музыки и привести их в некую стройную теоретическую кон­цепцию. В письме к И.П. Сахарову он сообщал: «Я ра­зобрал все до тонкости и могу указать в немногих руко­писях, бывших у меня под рукою, целую теорию нашей исконной мелодии и гармонию, отличную от Западной и весьма глубокую: работа была нелегкая: пробуя путь со всех концов, я испытал (!) начать прямо с акустики, и она вывела меня на свет Божий. Радуйтесь, радуйтесь!»
…>>

На стр. 319 книги В. Ф. Одоевский. Музыкально-литературное наследие, Москва, 1956:
<<…
В наших русских напевах должно отличать две эпохи: одна — древняя; к ней принадлежат песни старинные, вообще до-Петровские, и все сочиненные (сколько показали до­ныне исследования) не только в чисто диатонической гамме, но и в таких звукорядах, которые весьма сходны с доныне сохранившимися древними индийскими звукорядами.
… >>

И на стр. 328, 329
<<…
В числе доказательств, можно указать на весьма старин­ную, и едва ли не времен языческих, песню, столь общеиз­вестную во всей России: «Ай, мы просо сеяли».
…
У меня собрано несколько вариантов этой песни, и все они — чисто русские, не только принадлежат ко второму гласу, но состоят именно из тех нот, которые содержатся в одной из вышеупомянутых индийских погласиц; Джонес (Jones) обо­значает ее названием: Carnati; она состоит из следующих пяти звуковых элементов:

соль, ла, ут, ре, ми.

Эти только пять звуков мы находим и в песне: «Ай, мы просо сеяли»,

соль, ре ми, ре ут, ла, ми, ми, ми, ре ут, ре, ми, ут ре, ла ут, ре, ла.

Не любопытно ли такое сближение народностей, отдален­ных друг от друга и временем и пространством?
…>>

Там же на стр. 325:
<<…
Так напр[имер], очень часто встречающуюся в старинных наших напевах фразу:

ми, соль, ла

обыкновенно исправляют так:

ми, соль-диез, ла

и характеристическая, вполне правильная фраза обращается в пошлость
… >>

Это всё к тому, что музыка не обязательно возникает на почве усиленного обострения тяготений. В индийской музыке без танпура и сегодня не играют, а по моему разумению его неизменная и не утихающая на всём протяжении пьесы квинта создаёт набор опорных обертонов, во взаимодействии с которыми и развивается мелодия. Древнюю обертоновую основу, как способ самодостаточного существования, индийская музыка сохранила и по сей день, не в пример русской. И нельзя ведь сказать, что она бессвязно звучит. Обертоновая основа и чистая интонация предела более трёх музыки не портит, а придаёт ей особенные выразительные возможности. Нотация такой музыки дело хлопотное, и с этим в Индии похоже ещё много проблем.

Нашёл ноты.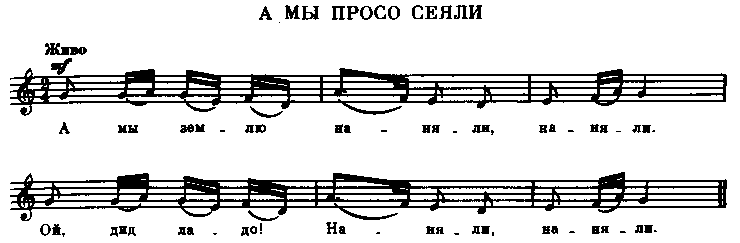



От версии данной Одоевским отличаются.

[commator]

Свободный Художник в сообщении #1102945 писал(а):

Интересно, что Modern Dorian Mode иногда называют "русским минором": https://en.wikipedia.org/wiki/Dorian_mode

Русским минором Балакирева, точнее.

Интересно, также, что

Одоевский 1868 по Бернандту 1956 писал(а):

В замечательном Сборнике Балакирева эта песня напеча-тана в двух видах, на стр. 18 и 20; их редакция весьма близ-ка к одному из записанных мною с голоса крестьян вариантов.

Представляем историкам, этнографам, филологам и археологам: во-первых, определить, хоть приблизительно, эпоху этой замечательной песни, кажется, намекающей на обычай увоза невест, — и разъяснить, наконец, что значат слова припева: дид ладо? а во-вторых, подвергнуть все представляемые музыкою данные исторической критике.

[commator]

Одоевский 1868 по Бернандту 1956 писал(а):

У меня собрано несколько вариантов этой песни, и все они — чисто русские, не только принадлежат ко второму гласу, но состоят именно из тех нот, которые содержатся в одной из вышеупомянутых индийских погласиц; Джонес (Jones) обозначает ее названием: Carnati*; она состоит из следующих пяти звуковых элементов:

соль, ла, ут, ре, ми¹.


¹ К сожалению, у нас нет в эту минуту под рукою книги Джонеса, но полагаем, что помещенная здесь уже давно сделанная выписка не содержит в себе ошибок.

*) Комментарий Издателя, с. 626: Carnati — южноиндийская музыкально-теоретическая система.

[commator]

commator в сообщении #1103523 писал(а):