Падение стержня у стенки

[Mihr]

mindroz в сообщении #1090428 писал(а):

$p=\frac{2}{3}m\sqrt{\frac{2gl}{3}}$

Отлично. Завершаем рассуждение. В конце падения (перед ударом о пол верхнего шарика) стержень ориентирован горизонтально. Следовательно, горизонтальные компоненты скорости (а потому и импульса) обоих шариков в этот момент равны (стержень ведь не растягивается и не сжимается). То есть, каждый из них имеет горизонтальную компоненту импульса, равную $p=\frac{1}{3}m\sqrt{\frac{2gl}{3}}$. Но у нижнего (правого) шарика помимо горизонтальной компоненты импульса никакой другой нет, то есть абсолютная величина его импульса и будет $p=\frac{1}{3}m\sqrt{\frac{2gl}{3}}$. Отсюда легко найти кинетическую энергию правого шарика в нужный нам момент времени. Вычитаем её из полной механической энергии системы $mgl$ и находим кинетическую энергию левого шарика. Отсюда находим его скорость.

Пожалуйста, досчитайте и напишите, что у Вас получилось.

[mindroz]

$E_{k2}=\frac{4mgl}{27}$
$E_{k1}=\frac{23mgl}{27}$
Конечная скорость $v$ равна
$v=\sqrt{\frac{46}{27}gl}$
Действительно, меньше, чем $\sqrt{2gl}$:).
А если у стержня не будет возможности оторваться от стенки, то скорость верхнего шарика в момент падения будет равна $\sqrt{2gl}$?

[Mihr]

mindroz в сообщении #1090434 писал(а):

$E_{k2}=\frac{4mgl}{27}$
$E_{k1}=\frac{23mgl}{27}$
Конечная скорость $v$ равна
$v=\sqrt{\frac{46}{27}gl}$

Имхо, Вы ошиблись, начиная с первой строчки.
Пересчитайте. Обратите, кстати, внимание на формулу $E_{k}=\frac{p^2}{2m}$. По ней зачастую считать удобнее.

mindroz в сообщении #1090434 писал(а):

А если у стержня не будет возможности оторваться от стенки, то скорость верхнего шарика в момент падения будет равна $\sqrt{2gl}$?

Да. Вы ведь сами это установили.

[mindroz]

У меня получился импульс $p=\frac{2}{3}m\sqrt{\frac{2gl}{3}}$, а у Вас, видимо, $p=\frac{1}{3}m\sqrt{\frac{2gl}{3}}$.

[Mihr]

mindroz в сообщении #1090437 писал(а):

У меня получился импульс $p=\frac{2}{3}m\sqrt{\frac{2gl}{3}}$, а у Вас, видимо, $p=\frac{1}{3}m\sqrt{\frac{2gl}{3}}$.

Так ведь импульс одного правого шарика (перед падением левого) и есть $p=\frac{1}{3}m\sqrt{\frac{2gl}{3}}$, я это подчёркивал. Величина $\frac{2}{3}m\sqrt{\frac{2gl}{3}}$ - это полный горизонтальный импульс системы. В конце движения этот импульс распределяется поровну между двумя шариками.

[mindroz]

Понял:).
$E_{k2}=\frac{mgl}{27}$
$E_{k1}=\frac{26mgl}{27}$
$v=\sqrt{\frac{52gl}{27}}$

-- 13.01.2016, 23:10 --

Большое спасибо за помощь! Очень понравилось Ваше решение, особенно конец:).

[Mihr]

На этот раз всё совпало. Ура.

[OlegCh]

Mihr в сообщении #1090442 писал(а):

На этот раз всё совпало. Ура.

Ээээ... А совпадает ли ваш ответ с ответом, если скорость искать через ЗСЭ с использованием формулы для кинетической энергии $K=\dfrac{MV^2}{2}+\dfrac{I\omega^2}{2}$, упомянутой уважаемым Димой М?

[Pphantom]

Сообщение dying отправилось в Карантин: «Из: Падение стержня у стенки»

[Mihr]

OlegCh в сообщении #1090682 писал(а):

Ээээ... А совпадает ли ваш ответ с ответом, если скорость искать через ЗСЭ с использованием формулы для кинетической энергии $K=\dfrac{MV^2}{2}+\dfrac{I\omega^2}{2}$, упомянутой уважаемым Димой М?

Решил указанным DimaM способом. У меня всё совпало точь-в-точь. Если хотите, могу предъявить своё решение.

[OlegCh]

Было бы интересно.

[Mihr]

OlegCh в сообщении #1090865 писал(а):

Было бы интересно.

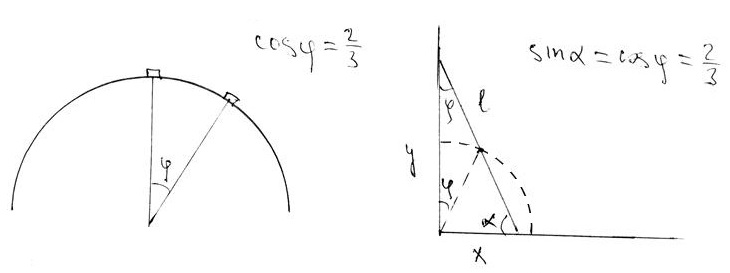
Рассмотрим сначала вспомогательную задачу с монетой, съезжающей без трения с полусферического купола радиуса $R$. В момент, когда радиус-вектор монеты (проведённый из центра полусферы), образует с вертикалью угол угол $\varphi$, потенциальная энергия монеты уменьшилась на величину $mgR(1-\cos(\varphi))$, и, значит, согласно закону сохранения энергии для скорости монеты справедливо соотношение
$\frac{mv^2}{2}=mgR(1-\cos(\varphi))$
откуда
$v^2=2gR(1-\cos(\varphi))$
и, значит, нормальное (центростремительное) ускорение
$a_n=\frac{v^2}{R}=2g(1-\cos(\varphi))$
С другой стороны, в момент отрыва от купола на монету действует лишь сила тяжести (так как сила нормальной реакции опоры обращается в нуль), следовательно, полное ускорение монеты в этот момент равно $g$, а нормальное (проекция полного ускорения на радиус полусферы) равно
$a_n=g\cos(\varphi)$.
Решая уравнение
$g\cos(\varphi)=2g(1-\cos(\varphi))$,
получаем
$\cos(\varphi)=\frac{2}{3}$.
При соответствующем значении угла происходит отрыв монеты от купола.

В нашем решении задачи со штангой разгон нижнего груза продолжается до значения $y=\frac{2}{3}l$, откуда $\sin(\alpha)=\frac{2}{3}$, и, значит, по формулам приведения $\cos(\varphi)=\frac{2}{3}$. То есть, отрыв верхнего груза от вертикальной опоры происходит при том же самом значении угла $\varphi$.
Найдём угловую скорость центра масс системы в этот момент. Имеем
$K=\frac{2mv^2}{2}+\frac{J\omega^2}{2}$,
где
$J=2m(\frac{l}{2})^2$
и
$v=\omega\frac{l}{2}$.
Подставляя указанные значения скорости центра масс и момента инерции в выражение для кинетической энергии, получаем после упрощения
$K=\frac{ml^2\omega^2}{2}$,
поэтому на основании закона сохранения энергии имеем
$mgl(1-\cos(\varphi))=\frac{ml^2\omega^2}{2}$.
Отсюда
$\omega^2=\frac{2g(1-\cos(\varphi))}{l}$.
Подставив сюда значение $\cos(\varphi)=\frac{2}{3}$, получим значение угловой скорости центра масс в момент отрыва верхнего груза от опоры
$\omega=\sqrt{\frac{2g}{3l}}$.
Тогда абсолютное значение скорости центра масс в данный момент
$v_c=\omega\frac{l}{2}=\sqrt{\frac{gl}{6}}$,
а проекции этой скорости на координатные оси
$v_{cx}=\frac{2}{3}\sqrt{\frac{gl}{6}}$, $v_{cy}=-\frac{\sqrt5}{3}\sqrt{\frac{gl}{6}}$.
Штанга поворачивается вокруг центра масс с такой же угловой скоростью (но в обратном направлении), поэтому скорость нижнего конца штанги относительно центра масс в интересующий нас момент времени также равна по абсолютной величине
$u=\omega\frac{l}{2}=\sqrt{\frac{gl}{6}}$,
а проекции этой скорости на координатные оси
$u_x=\frac{2}{3}\sqrt{\frac{gl}{6}}$, $u_y=\frac{\sqrt5}{3}\sqrt{\frac{gl}{6}}$.
Складывая скорость центра масс со скоростью нижнего конца штанги относительно центра масс, получаем скорость нижнего конца штанги относительно поверхности. Компоненты этой скорости равны
$v_{2x}=\frac{4}{3}\sqrt{\frac{gl}{6}}$, $v_{2y}=0$.
Это в точности соответствует результату, полученному ТС:

mindroz в сообщении #1090428 писал(а):

$p=\frac{2}{3}m\sqrt{\frac{2gl}{3}}$

Дальше мы опирались лишь на закон сохранения энергии и на утверждение о том, что к моменту падения верхнего шарика горизонтальный импульс системы делится между шариками поровну.
Повторять эти рассуждения, думаю, незачем.

Есть ли ошибка в приведённых рассуждениях?

[OlegCh]

Mihr в сообщении #1090909 писал(а):

То есть, отрыв верхнего груза от вертикальной опоры происходит...

А почему, вы считаете, происходит отрыв?

[Mihr]

OlegCh в сообщении #1090915 писал(а):

А почему, вы считаете, происходит отрыв?

Мы получили, что $x$-компонента скорости (а значит и импульса) нижнего груза в некоторый момент времени достигла максимума. Следовательно, $x$-компонента его ускорения в этот момент равна нулю. Верхний груз до указанного момента времени двигался лишь вертикально: ни его скорость, ни ускорение не имели $x$-компоненты. Итак, в указанный момент времени изменение $x$-компоненты импульса прекратилось. Это значит, что исчезли горизонтальные силы, то есть верхний груз потерял контакт со стенкой.

[OlegCh]

Mihr в сообщении #1090921 писал(а):

Это значит, что исчезли горизонтальные силы, то есть верхний груз потерял контакт со стенкой.

И что? Что происходит дальше?