Yarkin писал(а):
Для

корни имют вид

и, если

- целое, то

и

- иррациональные.
А это почему? Понимаете, здесь я не смогу привести контрпример, иначе я бы опроверг теорему Ферма. Но доказанность при

настолько же отсутствует, как и при

. Вы лишь переформулировали формулировку.
P.S.
Уххх.....  Добавлено спустя 5 минут 26 секунд:
Добавлено спустя 5 минут 26 секунд:Хотя, пожалуй, в такой формулировке привести контрпример не сложно. Скажем, при

,
![$y=\sqrt[3]{7}$ $y=\sqrt[3]{7}$](https://dxdy-04.korotkov.co.uk/f/7/8/4/7843c2d9a029d7181583ed868161aa7882.png)
,
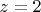
, имеем

, и имеем всё тот же треугольник, но при этом иррациональным будет только
одно из чисел

и

, а не
оба, как вы утверждали:
Цитата:
если

- целое, то

и

- иррациональные.
Более того, ясно, что число
 бывает
бывает рациональным (хотя бы потому, что функция

непрерывна, и, следовательно, принимает все промежуточные значения). Так что проблема --- как раз в том, чтобы доказать, что

и

не могут быть рациональными
одновременно.