Если рассматривать
все заряды системы, то из уравнений исчезают

и





Но что значит "рассматривать все заряды"? Ну допустим решая задачку про некоторое небольшое количество зарядов в вакууме это сделать можно. Но заряды в веществе? Это для "нейтрального проводника" вместо усредненных

вам придется аккуратно расписать в виде

и

каждый протончик и электрончик и все это подставить в уравнения. Мало того что это утомительно, по современным представлениями это и вовсе невозможно. Представлять каждый протончик и электрончик в виде механически движущихся шариков с какой то плотностью заряда некорректно.
Поэтому львиную долю этих зарядов, пользуясь тем что среднее поведение их в малом участке вещества схоже между собой, описывают через их "совместное поведение"
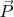
и

.
Некоторое подмножество зарядов

, обладающее в среднем нулевыми плотностью заряда и плотностью тока, описываются как "плотность количества протекшего заряда"

, где интеграл отсчитывается от условного момента

когда плотность этого подмножества зарядов была везде строго нулевой. Плотность заряда и плотность тока из этой величины легко восстанавливаются

,

Другое подмножество зарядов с нулевой плотностью заряда

(уже не в среднем а всегда) и ненулевой плотностью чисто вихревого тока, который по этой причине можно выразить как ротор от другой величины

.
Таким образом уравнения, с разбиением зарядов на описанные подгруппы, можно переписать в виде


Если теперь ввести обозначения

для "электрического поля за вычетом той его части, которая создана второй подгруппой зарядов"

и

для "магнитного поля за вычетом той его части, которая создана третьей подгруппой зарядов"

(умножив вышеопределенное

на

для подгонки к более удобной размерности) то и получим запись


То что
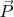
используется традиционно для описания диэлектриков а

магнетиков - не догма. Вы можете нейтральное проводящее кольцо с постоянным током описать и через

с нулевыми
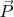
,

. Можете через линейно растущее
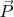
с нулевыми

,

. Можете через

с нулевыми

,
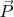
и все три описания дадут один и тот же результат. А можете разбить ток на три произвольные части и каждую описать своим способом. Как разбивать заряды на подгруппы - дело ваше. Другое дело что скажем в магнетиках величина

не своей жизнью живет а зависит от

и там такое описание более оправдано



