У вас два заряда. Один с плюсом, другой с минусом. Исправляйте снова

Даже не знаю, после интегрирования получается именно то, что я написал, может есть какие-то нюансы при интегрирования производной от дельта функции

? Минус у меня появился от умножения на
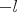
, для того чтобы образовать производную от дельта-функции.
берите градиент от выражения для потенциала без дельта-функций. Дельта-функции появятся от

и

(у меня выше в знаменателе стоит

, должно быть

).
Спасибо, ваш вариант проще, но хотелось бы использовать наработку с потенциалом с дельта функцией, а то зря что ли я его уже 2 страницы вывожу

А дальше уже можно плясать и в обратную сторону.
А можете раскрыть тайну, что за такая обратная сторона, про которую вы говорите, а то я "темнота" что-то не понял
