Асимпт. плотность решений диофантовых уравнений

[Brukvalub]

vicvolf в сообщении #1036672 писал(а):

Под диофантовым уравнением от $k$ переменных понимается уравнение вида:
$F(x_1,...x_k)=0$, (1)
где все переменные принимают одновременно значения из области натуральных чисел, все коэффициенты и свободный член являются целыми числами, а степени являются натуральными числами.

Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

[vicvolf]

Brukvalub в сообщении #1039620 писал(а):

vicvolf в сообщении #1036672 писал(а):

Под диофантовым уравнением от $k$ переменных понимается уравнение вида:
$F(x_1,...x_k)=0$, (1)
где все переменные принимают одновременно значения из области натуральных чисел, все коэффициенты и свободный член являются целыми числами, а степени являются натуральными числами.

Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

Например, рациональная функция в числителе и знаменателе которой находятся многочлены, все коэффициенты и свободный член которых являются целыми числами, а степени являются натуральными числами.

[Deggial]

vicvolf, суть в том, что у Вас сейчас термин "диофантово уравнение" довольно расплывчатый. Например, $\tg n = m, n,m\in\mathbb{N}$ по-Вашему является диофантовым уравнением.

[Brukvalub]

vicvolf в сообщении #1039674 писал(а):

Brukvalub в сообщении #1039620 писал(а):

vicvolf в сообщении #1036672 писал(а):

Под диофантовым уравнением от $k$ переменных понимается уравнение вида:
$F(x_1,...x_k)=0$, (1)
где все переменные принимают одновременно значения из области натуральных чисел, все коэффициенты и свободный член являются целыми числами, а степени являются натуральными числами.

Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

Например, рациональная функция в числителе и знаменателе которой находятся многочлены, все коэффициенты и свободный член которых являются целыми числами, а степени являются натуральными числами.

Приведенный пример не исчерпывает всех ситуаций, попадающих под ваше "определение" диофантова уравнения, поэтому мой вопрос не снят.
Повторяю вопрос:
Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

[vicvolf]

Deggial в сообщении #1039706 писал(а):

vicvolf, суть в том, что у Вас сейчас термин "диофантово уравнение" довольно расплывчатый. Например, $\tg n = m, n,m\in\mathbb{N}$ по-Вашему является диофантовым уравнением.

Под диофантовым уравнением от $k$- переменных в данной работе понимается уравнение $F(x_1,...x_k)=0$, где функция, стоящая слева, принимает целочисленные значения при натуральных (целочисленных - оговаривается особо) значениях всех входящих в нее аргументов.
Уравнение $\tg n = m, n,m\in\mathbb{N}$ не является диофантовым в смысле данного определения, так как функция $\tg(n)$ не принимает целочисленные значения при натуральных значениях $n$. Однако, тригонометрические уравнения $\tg(\pi/4+2\pi n)=0$ и $\tg(-\pi/4+2\pi n)=0$ являются диофантовыми по данному определению, так как тригонометрические функции в указанных уравнениях принимают целочисленные значения при натуральных значениях $n$.

-- 24.07.2015, 11:34 --

Brukvalub в сообщении #1039711 писал(а):

Приведенный пример не исчерпывает всех ситуаций, попадающих под ваше "определение" диофантова уравнения, поэтому мой вопрос не снят.
Повторяю вопрос:
Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

Согласен, это не корректно сказано. Однако, эти уточнения не нужны в смысле данного выше определения диофантова уравнения.

[Brukvalub]

Вы сами себе противоречите. Сейчас вы утверждаете, что

vicvolf в сообщении #1040089 писал(а):

Под диофантовым уравнением от $k$- переменных в данной работе понимается уравнение $F(x_1,...x_k)=0$, где функция, стоящая слева, принимает целочисленные значения при натуральных (целочисленных - оговаривается особо) значениях всех входящих в нее аргументов.

Но ранее вы писали:

vicvolf в сообщении #1039674 писал(а):

Brukvalub в сообщении #1039620 писал(а):

vicvolf в сообщении #1036672 писал(а):

Под диофантовым уравнением от $k$ переменных понимается уравнение вида:
$F(x_1,...x_k)=0$, (1)
где все переменные принимают одновременно значения из области натуральных чисел, все коэффициенты и свободный член являются целыми числами, а степени являются натуральными числами.

Что такое "коэффициент функции"? Что такое "свободный член" функции? Что такое "степень" функции?

Например, рациональная функция в числителе и знаменателе которой находятся многочлены, все коэффициенты и свободный член которых являются целыми числами, а степени являются натуральными числами.

С одной стороны, согласно приведенному примеру, получается, что уравнение$ \frac{x+1}{x+2}=0 $является диофантовым, с другой стороны, функция в его левой части принимает много НЕ целочисленных значений для натуральных значений аргумента, значит, оно не является диофантовым. Я совсем запутался...

vicvolf в сообщении #1040089 писал(а):

Однако, тригонометрические уравнения $\tg(\pi/4+2\pi n)=0$ и $\tg(-\pi/4+2\pi n)=0$ являются диофантовыми по данному определению, так как тригонометрические функции в указанных уравнениях принимают целочисленные значения при натуральных значениях $n$.

Пока не оговорено, что такое "коэффициент уравнения", данное уравнение нельзя признать диофантовым, поскольку в нем присутствует число $\pi$, а вдруг, это "коэффициент уравнения" (по крайней мере, это число ОЧЕНЬ похоже на коэффициент, как его проходят в 6-м классе общеобразовательной школы)?
Может, вам сначала разобраться в задах теории диофантовых уравнений, подтянуть определения основных понятий, а уж потом излагать нам здесь свои "могучие изыскания в передовых областях теории чисел"?
Пока - незачОт!

[nnosipov]

Вот диофантово (в любых смыслах) уравнение: $y(2y^2-x^2)-x-c=0$, где $c \neq 0$ --- целочисленный параметр. vicvolf, что Ваши теоремы позволяют утверждать о количестве целочисленных решений $(x,y)$ этого уравнения? Как это количество зависит от параметра $c$? Более конкретно: можно ли с помощью Ваших теорем доказать, что при фиксированном значении $c$ множество решений конечно? Ответьте, пожалуйста.

[vicvolf]

nnosipov в сообщении #1040102 писал(а):

Вот диофантово (в любых смыслах) уравнение: $y(2y^2-x^2)-x-c=0$, где $c \neq 0$ --- целочисленный параметр. vicvolf, что Ваши теоремы позволяют утверждать о количестве целочисленных решений $(x,y)$ этого уравнения? Как это количество зависит от параметра $c$? Более конкретно: можно ли с помощью Ваших теорем доказать, что при фиксированном значении $c$ множество решений конечно? Ответьте, пожалуйста.

Здесь скорее поможет теорема Зигеля о конечном числе целых точек на кривой $f(x,y)=0$ над полем рациональных чисел, если род кривой $p>0$.
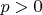
В моей работе меня больше интересовали диофантовы уравнения с бесконечным количеством натуральных решений, так как целью работы являлось доказательство, что асимптотическая плотность количества натуральных решений различных классов диофантовых уравнений равна 0. В случае конечного числа решений, асимптотическая плотность количества решений данного диофантового уравнения очевидно равна 0. Для алгебраического диофантова уравнения степени $n$ от $k$ переменных я нашел оценку сверху количества решений в гиперкубе размерности $k$ со стороной длиной $N$ ($N$- натуральное число) и показал, что указанная оценка равна $\pi(B_N) \leq n\cdot N^{k-1}$, а асимптотическая плотность количества решений $\lim_{N \to \infty} (n\cdot N^{k-1}/N^k)=0$. Указанная оценка достигается в вырожденном случае, когда поверхность, соответствующая диофантову уравнению, представляет из себя $n$ взаимно параллельных или перпендикулярных гиперплоскостей, параллельных гиперплоскостям координат и проходящих через первый квадрант. В частном случае при $k=2,n=3$ выполняется оценка $\pi(B_N) \leq 3 N$. Указанная оценка соответствует 3 взаимно параллельным или перпендикулярным прямым параллельным осям координат, проходящим через первый квадрант. Например, диофантово уравнение $(y-a)(y-b)(x-c)=0$, где $a,b,c$ - натуральные числа.

[nnosipov]

vicvolf в сообщении #1040449 писал(а):

Здесь скорее поможет теорема Зигеля о конечном числе целых точек на кривой $f(x,y)=0$ над полем рациональных чисел, если род кривой $p>0$.

Таким образом, Ваши теоремы здесь бесполезны. А ведь эта задача эффективно решается вполне школьными средствами, и дубинка (неэффективная к тому же) вроде метода Зигеля здесь совершенно неуместна.

vicvolf в сообщении #1040449 писал(а):

В частном случае при $k=2,n=3$ выполняется оценка $\pi(B_N) \leq 3 N$

Это очень слабый результат, ценность его равна нулю, поскольку он очень далёк от действительности (даже в элементарном случае $n=2$).

vicvolf в сообщении #1040449 писал(а):

Например, диофантово уравнение $(y-a)(y-b)(x-c)=0$, где $a,b,c$ - натуральные числа.

Назвать это уравнение диофантовым --- это пойти в ресторан не то что без галстука, а вообще без штанов. Ну, это же неприлично просто. Что такое диофантовы уравнения, можно узнать из книги Спринджука "Классические диофантовы уравнения от двух неизвестных". Загляните хотя бы в оглавление.

[vicvolf]

nnosipov в сообщении #1040477 писал(а):

vicvolf в сообщении #1040449 писал(а):

Например, диофантово уравнение $(y-a)(y-b)(x-c)=0$, где $a,b,c$ - натуральные числа.

Назвать это уравнение диофантовым --- это пойти в ресторан не то что без галстука, а вообще без штанов. Ну, это же неприлично просто. Что такое диофантовы уравнения, можно узнать из книги Спринджука "Классические диофантовы уравнения от двух неизвестных". Загляните хотя бы в оглавление.

Спасибо, заглянул. Добавление в определение алгебраического диофантова уравнения (ДУ) требования неприводимости многочлена по сравнению с общепринятым определением https://ru.wikipedia.org/wiki/%D0%94%D0 ... 0%B8%D0%B5 значительно сокращает количество его решений вплоть до конечного. Если автор рассматривает только такие ДУ, то он конечно имеет на это право. Если Вы рассматриваете тоже только такие ДУ, то тоже имеете на это право, но вот требовать от других рассмотрения только таких ДУ Вы не в праве. Например, Бухштаб на стр.268 в теореме 274 о конечности числа решений одного алгебраического ДУ отдельно оговаривает требование неприводимости многочлена, т.е он его не подразумевает по определению. В известной теореме: "Уравнение $a_1x_1^{n_1}+...+a_k x_k^{n_k}=0$, где $k \geq 2,n_1,...n_k$- натуральные числа, а $a_1,...a_k$- целые числа, $a_1>0,a_2+...a_k<0$,$n_1$ и $n_2 \cdot n_3....\cdot n_k$ взимно простые, имеет бесконечное множество решений в натуральных числа."(Серпинский стр. 85) и других теоремах о ДУ не содержится требование о неприводимости многочлена. Что эти теоремы не о диофантовых уравнениях? Извините, но при всем уважении к Вам, я не могу с этим согласиться и использую общепринятое определение. В этом смысле уравнение $(y-a)(y-b)(x-c)=0$, где $a,b,c$ - натуральные числа, является диофантовым, так как функция слева принимает целочисленные значения при целых значениях неизвестных.

nnosipov в сообщении #1040477 писал(а):

vicvolf в сообщении #1040449 писал(а):

В частном случае при $k=2,n=3$ выполняется оценка $\pi(B_N) \leq 3 N$

Это очень слабый результат, ценность его равна нулю, поскольку он очень далёк от действительности (даже в элементарном случае $n=2$).

Это точный результат, так как количество решений уравнения $(y-a)(y-b)(x-c)=0$ ( $a,b,c$ - натуральные числа) в натуральных числах в квадрате со стороной длины N действительно равно $\pi(B_N) = 3 N$.

[nnosipov]

vicvolf в сообщении #1040697 писал(а):

Уравнение $a_1x_1^{n_1}+...+a_k x_k^{n_k}=0$, где $k \geq 2,n_1,...n_k$- натуральные числа, а $a_1,...a_k$- целые числа, $a_1>0,a_2+...a_k<0$,$n_1$ и $n_2 \cdot n_3....\cdot n_k$ взимно простые

Кстати, левая часть здесь действительно неприводима. Вы лучше приведите пример содержательной теоремы про диофантовы уравнения, где левая часть может быть приводимой. Требование неприводимости довольно естественно --- иначе уравнение распадается в несколько уравнений меньших степеней.

vicvolf в сообщении #1040697 писал(а):

Это точный результат

Да, в одном примитивном и потому неинтересном случае. Во всех остальных случаях он далёк от истинного положения дел. Даже для школьных уравнений вида $Axy+Bx+Cy+D=0$ (которые любят давать на районных олимпиадах) Ваши теоремы ничего содержательного не дают. Тогда кому и зачем они нужны?

Бывает, конечно, так, что и неточные результаты представляют определённый интерес (когда, например, проблема сложна, и получить даже грубый результат стоит многих усилий). Но в данном случае об этом не может быть и речи --- предложить доказать Вашу теорему в виде задачи не возьмут даже на районную школьную олимпиаду.

[vicvolf]

nnosipov в сообщении #1040764 писал(а):

Вы лучше приведите пример содержательной теоремы про диофантовы уравнения, где левая часть может быть приводимой.

Оценка количества решений для различных видов алгебраических уравнений не являлась целью данной части работы. Во второй части работы я займусь этим с помощью кругового метода Харди-Литлвуда.

nnosipov писал(а):

Ваши теоремы ничего содержательного не дают. Тогда кому и зачем они нужны?

Одной из целей данной части работы являлась нахождение максимального количества решений алгебраического диофантова уравнения от $k$ переменных степени $n$ и доказательство, что в этом случае асимптотическая плотность количества решений равна 0. Согласитесь с тем, что:
1. Факт, что асимптотическая плотность количества решений любого алгебраического диофантова уравнения с бесконечным числом решений равна 0, не является очевидным.
2. Данный результат получен впервые.

[nnosipov]

vicvolf в сообщении #1041011 писал(а):

Согласитесь с тем, что:
1. Факт, что асимптотическая плотность количества решений любого алгебраического диофантова уравнения с бесконечным числом решений равна 0, не является очевидным.
2. Данный результат получен впервые.

Этот факт очевиден до неприличия. Никому в голову не придётся выставлять его как "результат работы". Это просто смешно (обратите внимание на комментарии выше по поводу этого якобы результата).