Кроме энергии есть еще одна сохраняющаяся величина.
Есть ещё импульс. Но тут я не могу ничего толкового придумать.
На земной орбите корабль будет иметь импульс

. На промежуточной орбите корабль будет обладать импульсом

.
Есть ещё второй закон Ньютона в импульсной форме

. Там сила вообще меняться будет, да и время некуда пристроить.
В общем, прошу ещё подсказку.
-- 19.07.2015, 14:34 --Задача №5Цитата:
Определите ближайший день наилучшей утренней видимости Венеры, зная гелиоцентрические долготы на 1 января Венеры (260°40') и Земли (99°55').
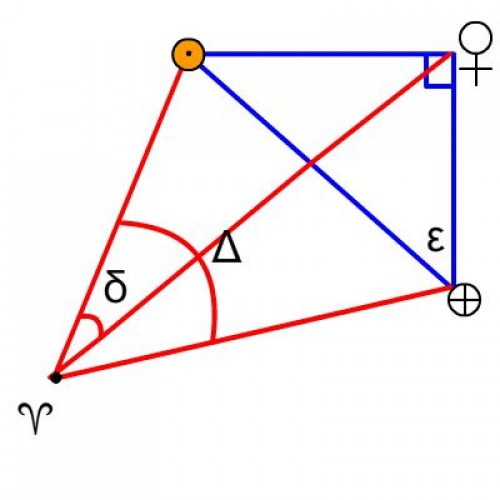
Правильно ли я нарисовал рисунок? Насколько я понимаю, наилучшая видимость Венеры будет достигнута в максимальной элонгации. Которая для Венеры определена и равна

.
Тогда, вот алгоритм решения:
1) Найти

и

(гелиоцентрические долготы Венеры и Земли), при которых угол

будет равен

.
2) Найти изменение гелиоцентрических долгот.
3) Связать это изменение с изменением времени.
4) Определить сколько времени прошло от 1 января.
Правильный ли этот алгоритм?



