Ах, Вам нужен пример, что возможно (почему то я прочел "обязательно"). Два примера
1) Вспомним следующее построение примера неизмеримого множества:

отождествляется с

разбивается на счетное число подмножеств, каждое из которых получается из другого сдвигом. Тогда если эти множества измеримы или неизмеримы одновременно, и в первом случае их меры равны. Тогда, ескли их меры равны

то мера

будет

, а если меры
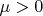
то мера

будет

(и это противоречие доказывает неизмеримость. Ясно, что ни одно из них не содержит подмножества положительной меры.
2) Пусть

ограничено и неизмеримо, но у него есть подмножества положительной меры. Пусть

супремум меры таких подмножеств. Тогда либо существует

с

, либо существуют

т.ч.

. Пусть во втором случае

. Тогда

измеримо и

. Ясно, что

искомое множество



