Конструкции-треугольники.
Я пытаюсь разобраться,в доказательстве из Ульянова. Оно там,для меня наиболее логичное,и понятное.
Сейчас ваше доказательство я понять не могу.. Вот почему:
1) Вот вы сейчас говорите,что красная и черная буквы не пересекаются.. а я вот на рисунке вижу обратное.. или у вас иное изображение?
2)
Цитата:
расстояние не меньше, чем длина самой маленькой конечности
И как это доказывается,это не очень,то очевидно..
-- 22.01.2015, 10:42 --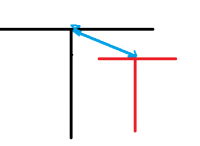
Т.е расстояние между этими двумя точками больше чем длина наименьшей конечности..
Ну,а как сие факт,мне поможет доказать,что множество букв Т на плоскости не более чем счетно?-я не вижу этого