========= ММ186 ========== Еще в школе, решая задачи типа "Из пунктов A и B навстречу друг другу...", грезил предлагаемой задачей. И вот...
ММ186 (7 баллов)
В 12:00 расстояние от маяка до сухогруза "Альфа" составляло

км, а до буксира "Омега" -

.
В 13:00 расстояния от маяка до "Альфы" и "Омеги" оказались такими же как 12:00. А в 14:00 расстояния от маяка до "Альфы" и "Омеги" оказались равны по

Найти минимальное расстояние от "Альфы" до "Омеги", учитывая, что в 13:45 смотритель маяка не видел "Омегу" за "Альфой".
Примечание: Сухогруз и буксир движутся прямолинейно и равномерно. Все плавсредства и маяк - материальные точки.
РешениеДежурно привожу аккуратные и подробные решения Олега Полубасова и Анатолия Казмерчука.
Решение Антона Никонова изложено не столь подробно. Зато он дальше всех продвинулся в деле обобщения задачи:
(Решение Антона Никонова)
Вначале расстояние от маяка до сухогруза "Альфа" составляло

метров, а до буксира "Омега" --

.
Спустя

секунд, расстояния от маяка до "Альфы" и "Омеги" составили

и

соответственно.
А через

секунд от начала, расстояния от маяка до "Альфы" и "Омеги" оказались равны

и

соответственно.
Найти минимальное расстояние от "Альфы" до "Омеги", учитывая, что через

секунд от начала, смотритель маяка не видел "Омегу" за "Альфой".
Примечание: Сухогруз и буксир движутся прямолинейно и равномерно. Все плавсредства и маяк - материальные точки.
--------------------------------------------------------------------------
Итак, необходимо найти функцию от 9 переменных.
Поставил маяк в начало декартовых координат. Довольно быстро пришёл к выводу, что результат зависит только от взаимного положения судов. Стало быть, направление движения одного из них можно задать произвольно.
Пусть "Омега" движется в этих координатах строго на восток со скоростью

на постоянной высоте

над горизонтальной осью. Тогда будут справедливы следующие уравнения:

















Постепенно разобравшись с левой и правой частями, всё-таки выразил

через известные величины, с помощью то ли чудовищной, то ли умопомрачительной формулы:

Работает! Найдя

благодаря этой неимоверной формуле, стало возможным вычислить неизвестные по вышеприведённым формулам.
Например, для исходной задачи:

метров.

метров.

метров.

метров.

(метра в секунду)

(км/ч).
А также вычислить соответствующие величины и для "Альфы", если тоже запустить её строго горизонтально на восток на высоте
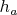
со скоростью

. Тогда для исходной задачи:

метров.

метров.

метров.

метров.

(метра в секунду)

(км/ч).
Теперь нетрудно найти расстояние

от маяка до "Омеги" в момент

(13:45) :


И расстояние от маяка до "Альфы" в момент

(13:45):

Синус угла между линией, соединяющей маяк с "Омегой" и горизонтальной осью в момент

(13:45)

, а косинус этого же угла

Синус угла между линией, соединяющей маяк с "Альфой" и горизонтальной осью в момент

(13:45)

, а косинус этого же угла

.
Разность между этими углами и есть тот самый угол, на который нужно повернуть траекторию движения "Альфы" относительно горизонтальной оси, чтобы условие затмения "Омеги" "Альфой" в момент

выполнилось.
Разница между горизонтальной составляющей скорости "Альфы" и горизонтальной составляющей скорости "Омеги" равна:

Поскольку вертикальная составляющая скорости "Омеги" равна нулю, разницу между вертикальными составляющими скорости "Альфы" и "Омеги" вычислить ещё проще:

Таков путь от "Альфы" до "Омеги" в момент

(13:45) по горизонтали:

А таков по вертикали:

Составил формулу изменения расстояния

от "Альфы" до "Омеги" в зависимости от времени

:


Приравняв производную к нулю, вычислил, сколько времени потребуется на достижение минимального расстояния от "Альфы" до "Омеги" после момента

(13:45) :

Подставив это значение в формулу изменения расстояния, получил
ответ на главный вопрос задачи. Минимальное расстояние от "Альфы" до "Омеги" находится так:

Для исходной задачи в

расстояние между "Альфой" и "Омегой" достигнет минимума в

метров.
Есть ещё вариант с пуском "Альфы" на север. Но для исходной задачи он даёт больший

метров.
Формулы позволяют найти минимум и для различных других значений

переменных

.
Признаюсь честно, потратив некоторое количество сил на разгадывание ребуса "какой буковкой что обозначено в решении Антона?", я сдался и решил поверить "на слово". Тем более, что схема решения в целом ясна, да и ответ для частного случая правильный

Интересно, что среди решавших ясно прослеживаются два "клана":
1. Найдем все нужные данные в двух известных треугольниках, а затем повернем (вокруг общей вершины в маяке) один по отношению к другому, так чтобы в 13:45 суда оказались на одной линии.
2. Сразу же выпишем законы движения обоих судов, а затем будем уточнять параметры, учитывая соотношения в условии.
Приведу точное значение обоих возможных ответов:

,

.
Почему эти ответы столь громоздки? Все как обычно. Я старался, что ответ был получше (не случайно же с условии появились корни). И подобрал соответствующие данные. Откуда при публикации выскочило другое время, в которое маяк и суда оказались на одной прямой, мне неизвестно. Но заметил я это лишь тогда, когда уже получил первое решение с ужасными ответами. После этого уточнять условие было бы не этично.
Олег Полубасов (отдельно от прилагаемого решения) нашел три момента времени сокрытия "Омеги" за "Альфой", в которые решение было бы хорошим и единственным.
Правда, два из них с оговорками:
Цитата:
Если считать, что при столкновении судов "Омегу" не будет видно за "Альфой", то дуали также не будет, если t=0 соответствует 14:00 или 11:00.
Понятно, что это не совсем то, что имел в виду я.
Третий вариант не содержит катастрофических последствий. Но если допустить, что "Омеги" не было видно в 12:30, то задача выхолащивается (суда движутся по параллельным фарватерам).
Я же хотел, чтобы двумерность задачи играла более существенную роль. И ради этого пошел даже на отказ от единственности решения. Поэтому время "ч" в неискаженном моей рассеянностью варианте условия не совпадало ни с 11:00, ни с 12:30, ни с 14:00.
Подводя итоги, можно сделать гипотетический вывод, что ответ будет хорошим, если суда окажутся на одной прямой с маяком в любой момент времени за исключением 13:45

Некоторые участники, найдя оба ответа, посчитали "главным" только меньший из них, поскольку в условии требовалось найти наименьшее расстояние. Конечно же, ответы равноправны. Вот если бы в условии было сказано "Найти наименьшее
возможное расстояне", тогда - другое дело.
И еще один курьез: уже после (правильного) нахождения наименьшего расстояния между судами один из участников отдельно выяснил, не столкнутся ли суда.
НаградыЗа правильное решение задачи ММ186 Антон Никонов получает призовых 10 баллов, Анатолий Казмерчук, Олег Полубасов и Сергей Половинкин - по 8 баллов, Виктор Филимоненков, Дмитрий Пашуткин и Евгений Гужавин - по 7 баллов.
Эстетическая оценка задачи 4.6 балла