Здравствуйте, извиняюсь, что долго не отвечал на вопросы и замечания.
Попытаюсь, может запоздало, ответить на вопросы и дать кой-какие комментарии.
Хотя на многие вопросы за меня уже ответили (спасибо им).
Это верно только если

- простое.
- молодец, прямо в точку...
Поясню.
или


,

При этих значениях

,

система уравнений

и при

,

превращается в систему тождественно равных уравнений:

А значит никакого противоречия быть не может.
Belfegor дальше задает вот такой вопрос:
(Цитатой воспользоваться не могу - при цитировании какие-то ошибки в формула, поэтому цитату выделю курсивом)
Alexey!
6. 
Я возвел первое уравнение этой системы в квадрат и вот что у меня получилось после ряда преобразований:

Что вы скажете об этом противоречии?
Это не противоречие.
6.

Первое уравнение системы

выполняется всегда - всегда существуют такие

и

, для которых

Допустим, что второе уравнение системы

не выполнимо,
тогда существуют такие

и

для которых справедливо следующее

Понятно, что

и

и получим следующее уравнение:

Ввиду парности простоты чисел

,

,

,

приходим к противоречию - не выполнима формула сокращенного умножения.
Кстати в рассуждениях у вас ошибка и её вам любезно указал участник
Алексей К. (за что ему большое спасибо).
А во-первых, я бы, конечно, попробовал (или не встревал бы), если бы Вы, кроме двух процитированных Вами равенств, процитировали бы и условие

.
Если

, то

, тогда

то

должно быть меньше

чего быть не может.
Как это, как это, как
это? Очень даже уместен.
Согласен.
Извините пожалуйста если обидел, я просто хотел сказать, что ошибка у меня в рассуждениях прежде всего - система п.6. справедлива только в тех случаях, если

- простое (на что мне и указал
venko), а ваш контрпример является следствием этой ошибки.
P.s. Всё бы ничего, но я догадывался что ошибка кроется именно в этом месте.
И я так долго не отвечал не вопросы по следующей причине.
Вместо пятого параграфа можно записать по-другому:
(особенно нижеследующее будет интересно почитать участнику под именем
Belfegor (молодец - к такому же противоречию придёт (или пришел уже)).
Рассмотрим следующий случай:
Alexey2 в сообщении #451988 писал(а):
...случай решения уравнения

, где ни один из членов

,

,

не делится на 3.
Хотя бы один из них делится.
Допустим

Тогда рассмотрим уравнение

, где





тогда:

,


где

и
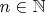

Но ведь не всегда

кратно трем.
Допустим

Тогда рассмотрим уравнение

, где





тогда:

,


где

и
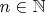

Можно рассмотреть и случай когда

- рассмотреть четвертое уравнение

и прийти к противоречию, а можно и не рассматривать (ввиду взаимозаменяемости

и

).
Основное противоречие:
"Если один из членов уравнения

кратен трем, то как минимум, ещё один из членов тоже кратен трём, чего быть не может
(Если рассматривать только примитивные тройки

,

и

, а если - не примитивные - то сократим на общий множитель и будем всё равно рассматривать примитивные)."