Цитата:
Definition
In the

-sphere

we choose a base point

. For a space

with base point

, we define
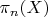
to be the set of homotopy classes of maps
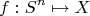
that map the base point a to the base point b. In particular, the equivalence classes are given by homotopies that are constant on the basepoint of the sphere. Equivalently, we can define
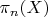
to be the group of homotopy classes of maps
![$g : [0,1]^n \mapsto X $ $g : [0,1]^n \mapsto X $](https://dxdy-01.korotkov.co.uk/f/8/e/c/8ec021a5f3de340f57b27cc3aae5840782.png)
from the

-cube to

that
take the boundary of the  -cube to
-cube to 
.
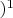
For
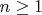
, the homotopy classes form a group. To define the group operation, recall that in the fundamental group, the product
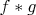
of two loops

and

is defined by setting
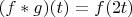
if

is in
![$[0,1/2] $ $[0,1/2] $](https://dxdy-01.korotkov.co.uk/f/0/9/f/09ff26ce6a7967389189386b5365ed1682.png)
and
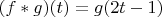
if

is in
![$[1/2,1]$ $[1/2,1]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe4325d38e849f6d71eac248bee0b4a582.png)
. The idea of composition in the fundamental group is that of following the first path and the second in succession, or, equivalently, setting their two domains together. The concept of composition that we want for the

-th homotopy group is the same, except that now the domains that we stick together are cubes, and we must glue them along a face.
We therefore define the sum of maps ![$f, g : [0,1]^n \mapsto X$ $f, g : [0,1]^n \mapsto X$](https://dxdy-04.korotkov.co.uk/f/f/8/7/f87cc997c1290a63c0df59ca27dcf7ac82.png) by the formula
by the formula  for
for ![$t_1 \in [0,1/2]$ $t_1 \in [0,1/2]$](https://dxdy-03.korotkov.co.uk/f/2/1/1/21110d9de91d230526715e694f88b03f82.png) and
and  for
for ![$t_1 \in [1/2,1]$ $t_1 \in [1/2,1]$](https://dxdy-01.korotkov.co.uk/f/8/4/4/8447f1780605c5e882040db27b1574ec82.png) .
.  For the corresponding definition in terms of spheres, define the sum
For the corresponding definition in terms of spheres, define the sum  of maps
of maps to be
to be  composed with
composed with  , where
, where  is the map from
is the map from  to the wedge sum of two
to the wedge sum of two  -spheres that collapses the equator and
-spheres that collapses the equator and  is the map from the wedge sum of two
is the map from the wedge sum of two  -spheres to
-spheres to  that is defined to be
that is defined to be  on the first sphere and
on the first sphere and  on the second.
on the second.
If
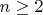
, then
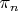
is abelian. (For a proof of this, note that in two dimensions or greater, two homotopies can be "rotated" around each other. See Eckmann-Hilton argument)
- Надо понимать, что мы берем что-то типа капли. Да?
- Получается что-то типа капель имеющих одно и то же основание. Правильно?
- Муть с сферами пропускаю. Too many errors...

пусть
![$[X,Y]$ $[X,Y]$](https://dxdy-04.korotkov.co.uk/f/3/4/3/3430a3895103dd13a1cdf2b4f637e16582.png)
-- множество классов гомотопных отображений
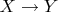
Т.е. любые два гомотопных отображения мы отождествляем.
Если
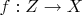
-- непрерывное отображение, то возникает отображение
![$f_\ast:[X,Y]\to [Z,Y]$ $f_\ast:[X,Y]\to [Z,Y]$](https://dxdy-02.korotkov.co.uk/f/5/0/c/50cc3e01db4f2df16e27e6aeb6e54fe382.png)
по правилу
![$f_\ast([F])=[F\circ f]$ $f_\ast([F])=[F\circ f]$](https://dxdy-01.korotkov.co.uk/f/4/2/9/42989b93279ed1cd8e235e5e4178126882.png)
(квадратные скобки означают класс отображения)
Это я понимаю так. Пусть
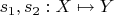
какие-то отображения. Рассматриваем отображения
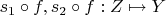
.
Если

и

пренадлежат одному классу,то очевидно
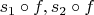
тоже принадлежат одному классу(уже среди классов
![$[Z,Y]$ $[Z,Y]$](https://dxdy-02.korotkov.co.uk/f/d/b/1/db1a24ecb1417de07ccb004c04f4fef282.png)
). Обратное, вообще говоря, неверно. Таким образом
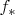
определяет гомоморфизм классов эквивалентности
![$[X,Y]$ $[X,Y]$](https://dxdy-04.korotkov.co.uk/f/3/4/3/3430a3895103dd13a1cdf2b4f637e16582.png)
на
![$[Z,Y]$ $[Z,Y]$](https://dxdy-02.korotkov.co.uk/f/d/b/1/db1a24ecb1417de07ccb004c04f4fef282.png)
(или его подмножества).
Аналогично, если
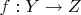
-- непрерывное отображение, то возникает отображение
![$f^\ast:[X,Y]\to [X,Z]$ $f^\ast:[X,Y]\to [X,Z]$](https://dxdy-03.korotkov.co.uk/f/a/2/f/a2f16acab7a60868d8aa24b9442e7f5282.png)
по правилу
![$f^\ast([F])=[f\circ F]$ $f^\ast([F])=[f\circ F]$](https://dxdy-02.korotkov.co.uk/f/9/7/1/971132baa5b147e4544916565dcd522982.png)
См. выше. Т.е. построили гомоморфизм классов эквивалентности
![$[X,Y]$ $[X,Y]$](https://dxdy-04.korotkov.co.uk/f/3/4/3/3430a3895103dd13a1cdf2b4f637e16582.png)
на
![$[X,Z]$ $[X,Z]$](https://dxdy-02.korotkov.co.uk/f/5/e/4/5e45a1451ae504101aaab22bdc0e175e82.png)
.
Так вот

и

гомотопически эквивалентны, если для любого

имеется взаимнооднозначное соответствие
![$[X,Y]\to [X',Y]$ $[X,Y]\to [X',Y]$](https://dxdy-02.korotkov.co.uk/f/5/f/7/5f7b55cb508c258b0579636df028a6af82.png)
(можно и по второму аргументу -- равносильно)
Т.е. берем какое-то третье пространство

, рассматриваем всевозможные отображения
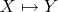
и
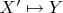
и разбиваем их на классы эквивалентности. Если для всех

у нас будут получатся изморфные классы, тогда

и
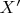
будут гомотопически эквивалентны. Правильно?
А причем тут предыдущие 2 предложения про
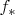
и
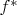
?