Вот и славно, что мы все согласовали. А почему с таким трудом согласовывали подобные пустяки? Да, это, конечно, пустяки, но
в неизведанном лесу. А в таком лесу обычная коряга может запросто привидиться страшным лешим.
Вы забывате включить в возможные начальные условия и различные векторы ускорения.
То есть
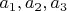
- это тоже
переменные, удовлетворяющие уравнениям

Тогда да, инвариантность будет. Если вращения задевают и эти переменные.
Это пример
неизведанности леса. Ведь я трактую вектор ускорения

как характеристику конкретной частицы, которая вполне определена и является
постоянной величиной. Поэтому мне не приходило в голову писать уравнения для этого вектора.
Но и Вы тоже правы. Нам никто не запрещает писать уравнения для этого вектора. Логически, можно и так и так.
И, конечно, Вы правы в том, что в уравнении движения

- это
переменная. Но вместо переменной можно подставлять константы (как делаю я), а можно переменные (как делаете Вы).
Тогда уж можно сразу записать уравнение

Да, конечно. Но это опять пример того же рода. И дело вкуса. Например,
myhand любит такие уравнения. А я нет, но привыкаю.
Резюмируя, в этом лесу
пока еще нет традиций и устоявшейся терминологии. Поэтому у нас были и будут соответствующие трудности.