Iosif1 писал(а):

писал:
Цитата:
Я не знаю, как Вы считаете там нулевые разряды. Ошибку в своих рассуждениях ищите сами.
Вы рассматриваете предполагаемую разность как точный куб.
И все обязано получиться.
Какую разность?

? Разумеется. Мы ведь пытаемся "от противного" доказать теорему Ферма, то есть, предполагаем, что равенство

для некоторых натуральных

,

,
 выполняется
выполняется. И выводим из этого следствия, надеясь получить противоречие. В частности, разность

обязана быть точным кубом. Если же эта разность не является точным кубом, то есть, числа

,

,

не удовлетворяют равенству

, то может быть что угодно, но тогда они не имеют ни малейшего отношения к теореме Ферма.
Iosif1 писал(а):
Вы уверены, что у Вас получится именно такой

, который запланирован состоявшимся равенством.
Число

определяестя равенством

. Оно именно таким и должно быть, так как Вы приводите наше равенство к виду

. И другим это число не может быть. Если мы возьмём другое число, оно не будет иметь никакого отношения к теореме Ферма.
Iosif1 писал(а):
А ваше равенство состоялось только на малых разрядах.
Вы же сами пожелали ограничиться только младшими разрядами, хотя я Вам пару раз объяснял, что это бесперспективно. Таким образом можно доказать некоторые частные случаи теоремы Ферма, но полного доказательства не получится.
Iosif1 писал(а):
А предлагаемый мной вариант расчета учитывает то, что есть на самом деле.
Это Вы только воображаете. На самом деле Вы также ограничиваетесь только младшими разрядами. Причём, совершенно явно. Где Вы используете старшие разряды? Указать не сможете.
Iosif1 писал(а):
Вы в формализованном виде рассматриваете такую возможность, чтобы количество нулевых разрядов в величине

было заданным.
Ничего подобного. Мы рассматриваем случай, когда число

делится на

, но не делится на

, то есть, при записи в троичной системе счисления оканчивается на два нуля. Количество нулевых разрядов в числе

определяется после этого однозначно. Как
оказывается, в этом случае число

в троичной записи оканчивается на
один ноль.
Iosif1 писал(а):
Вы изначально, априори предполагаете, что такое равенство возможно.
Ну уж такой у нас метод доказательства - "от противного". То есть, мы предполагаем, что равенство выполняется, и пытаемся из этого вывести противоречие. Если мы не будем предполагать, что равенство выполняется, то наши вычисления не будут иметь никакого отношения к теореме Ферма.
Iosif1 писал(а):
Вы как и те великие не верите в эффективность использования

-того счисления и пренебрегаете им.
Я довольно долго и безуспешно пытался Вам втолковать, что правильное название - не "

-тое счисление", а "

-ичная система счисления". Это общепринятый и общеизвестный термин.
Что касается "эффективности", то для Вас она состоит в том, что такая запись явно показывает делимость на степени числа

, и более, пожалуй, ни в чём. Всё это очень хорошо можно увидеть и без использования такой системы счисления, что я Вам
демонстрировал.
Iosif1 писал(а):
Взятие производных стало возможно благодаря возможности пренебрежения бесконечно малыми.
Здесь же пренебрежение большими разрядами не допустимо.
Старшими разрядами пренебрегаете Вы сами. Это Ваша идея (но Вы здесь далеко не первый), по моему (и не только моему) мнению, совершенно безнадёжная. Младшие же разряды всех рассматриваемых выражений определяются младшими разрядами чисел

,

,

. Так что, если мы рассматриваем во всех выражениях только младшие разряды, то старшие разряды нам не понадобятся (вопрос только в количестве требуемых младших разрядов).
Iosif1 писал(а):
Пока я писал пришел еще ответ.
Вы

пишите:
Цитата:
Вот здесь Вы и врёте. Посмотрите: у меня
получилось не два нуля, а только один. И в
примере тоже один (величина

). А после прибавления

(или, в другом варианте,

) становится четыре. Зачем Вам вообще нужна эта сумма квадратов, если это всего-навсего

или

? Вы просто себя запутываете этой суммой квадратов и не можете правильно их просуммировать. Хотя всякому должно быть ясно, что ничего суммировать не надо, если для суммы есть явное и очень простое выражение.
Давайте на примерах.
Я позволил себе восстановить цитату из моего
сообщения в первоначальном виде.
Iosif1 писал(а):
...
Я приводил этот пример. Давайте по аналогии рвссмотрим вариант, когда основание

содержит два нулевых разряда.
Предположим, что основание равно

Поэтому младшие разряды

2.1
Поскольку у Вас

, то

, причём,
шестая цифра (скрытая за многоточием) - не

, так как

делится на

и не делится на

. Поэтому

,

, причём,
пятая цифра (скрытая за многоточием) - не

.
Iosif1 писал(а):

; 2.2
Насколько я помню, первоначально в этой сумме у Вас была арифметическая ошибка (в полном соответствии с приведённой выше цитатой из моего сообщения), а пока я по техническим причинам с 27 июля сидел без связи, Вы эту ошибку исправили. И хорошо, что исправили. Теперь видно, что эта сумма - всего лишь

, и что не было никакой пользы от суммирования квадратов вместо применения простой готовой формулы - также в соответствии с тем, что я писал в той цитате.
Iosif1 писал(а):
Умножаем результат, полученный в 2.2 на восемь, получаем:

2.3
Теперь производим сложение 2.3 и 2.1, получаем:

2.4
То есть мы получаем и на этот раз в анализируемой сумме такое же количество нулевых разрядов, какое было в рассматриваемом основании. И так всегда!
Ничего не понял. Зачем умножать на

и прибавлять

? Мы рассматриваем равенство

, которое в Ваших обозначениях (при чётном

и, следовательно, нечётных

и

) имеет вид

. Складывая

и

, получим

, причём,
пятая цифра (скрытая за многоточием) - не

. То есть,

оканчивается, как и положено, на
четыре нуля.
Iosif1 писал(а):
Но эта сумма промежуточная. Чтобы получить интересующий нас результат, необходимо прибавить и величину

.
В результате получаем:

То есть получаем результат с пятью, а не с четырьмя нулями в троичном счислении.
Ваша ошибка здесь, кстати, состоит в том, что на самом деле

, где
пятая цифра - не

, поэтому

, где
пятая цифра - не

, поэтому

, причём,
пятая цифра - не

. Так что нулей получается
четыре, как и должно быть. При сложении и вычитании не нужно забывать о невыписанных старших разрядах, которые могут быть ненулевыми. И, кстати, это Ваше

равно

, так что Вы просто запутываете себя усложнёнными вычислениями.
Iosif1 писал(а):
В этом то и есть найденное противоречие.
Для конкретного основания невозможно сконструировать и величину

и величину

; 2.5
с одинаковым количеством нулевых разрядов.
Выражение (2.5) оканчивается на
пять нулей (пятый ноль появляется после умножения на

),
выражение 
- тоже на
пять. В чём противоречие?
Iosif1 писал(а):
А ну Ваш контр пример, когда получается четыре нулевых разряда в анализируемой сумме при двух нулевых разрядах в выбранном основании.
Ведь Вы

пишете:
Цитата:
Совершенно невозможно понять, почему у Вас получается несоответствие в количестве нулевых разрядов, поскольку Вы этого не доказываете, а просто ссылаетесь на какие-то пробные расчёты, в то время как в моих расчётах - и численных, и символьных - нулевых разрядов всегда ровно столько, сколько должно быть.
Как мы видели, в Ваших пробных расчётах имеется куча ошибок. И Вы, совершенно ни в чём не усомнившись, вываливаете эти расчёты на форум. В то время как я стараюсь тщательно проверять свои расчёты, а если обнаруживается какое-то несоответствие, то не успокоюсь, пока не разберусь, в чём дело. Поэтому мой контрпример правильный, а Ваши "доказательства" - просто скопище ошибок.
Ещё раз хочу подчеркнуть, что доказать теорему Ферма, основываясь на рассмотрении только младших разрядов чисел в какой-нибудь системе счисления, невозможно. Известно, что уравнение Ферма

при простом

имеет решения по любому модулю (то есть, в любом кольце

), а также в кольцах целых

-адических чисел. К сожалению, деталей я не знаю и не уверен, что эта формулировка точная, однако примерно о том же
пишет Руст. Я покажу процедуру подбора решений уравнения

по модулю

для случая, когда число

делится на

, но не делится на

, на языке системы Mathematica.
Исходными являются соотношения

,

,

, где

,

,

- некоторые натуральные числа. Из них выражаем

,

,

.
Предположим, что мы подобрали

,

(с

цифрами в троичной системе счисления) и

(с

цифрами) так, что выполняется сравнение

Подберём следующие цифры:

,

,

. Должно выполняться сравнение

Используя возможности системы Mathematica и затратив некоторое время на изучение чрезвычайно длинного в развёрнутом виде выражения
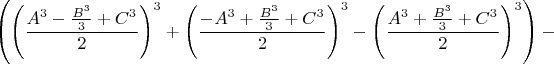

можно выяснить, что должно быть

, и что для

будет

. Это позволяет использовать следующие процедуры подбора.
Функция, подбирающая начальные значения

,

,

:
Код:
Strt[]:=Module[{A0,B0,C0,d,x,y,z},
d=PowerMod[2,-1,3^7];
Label[One];A0=Random[Integer,{1,3^6-1}];
If[Mod[A0,3]==0,Goto[One]];
B0=3^2Random[Integer,{1,2}];
Label[Two];C0=Random[Integer,{1,3^6-1}];
If[Mod[С0,3]==0,Goto[Two]];
a=Mod[d(A0^3-B0^3/3+C0^3),3^7];
b=Mod[d(-A0^3+B0^3/3+C0^3),3^7];
c=Mod[d(A0^3+B0^3/3+C0^3),3^7];
If[Mod[a^3+b^3-c^3,3^8]≠0,Goto[One]];
{A0,B0,C0,a,b,c}]
Функция, подбирающая следующие цифры:
Код:
FDF[ABC_,m_]:=Module[{A0,B0,C0,A1,B1,C1,a,b,c,d,T},
d=PowerMod[2,-1,3^(7+m)];
Label[Three];A1=Random[Integer,{0,2}];
A0=3^(5+m)A1+ABC[[1]];
B1=Random[Integer,{0,2}];
B0=3^(2+m)B1+ABC[[2]];
C1=Random[Integer,{0,2}];
C0=3^(5+m)C1+ABC[[3]];
a=Mod[d(A0^3-B0^3/3+C0^3),3^(7+m)];
b=Mod[d(-A0^3+B0^3/3+C0^3),3^(7+m)];
c=Mod[d(A0^3+B0^3/3+C0^3),3^(7+m)];
If[Mod[a^3+b^3-c^3,3^(8+m)]≠0,Goto[Three]];
{A0,B0,C0,a,b,c}]
Функция, подбирающая числа

и

с

троичными цифрами, а число

- с

троичными цифрами (из которых

- нули в младших разрядах):
Код:
FD[n_]:=Module[{ABC,m},
ABC=Strt[];
For[m=1,m≤n,m++,ABC=FDF[ABC,m]];
ABC]
При этом числа

,

,

будут с

цифрами, а равенство

будет выполняться по модулю

.
Заметим, что

младших цифр числа

определяют

цифр числа

, поэтому фактически в сравнении

участвуют только

цифр числа

. Как я однажды
писал, это может привести к тому, что некоторые равенства могут выполняться с меньшим количеством цифр (с

).
Пример использования процедуры FD[n]:
Код:
BaseForm[FD[53],3]
Результат:
Код:
{22102021210100110210001221002001101122011020000100212021001_3,
1212111021012001212211210212211012100222102221111122200_3,
21212100121011201211221202001201111020112011011210000111111_3,
100001011000212012121010002212200012220000100200011122121201_3,
11211120202022220002100010222112010220100222001220121111200_3,
21011111111101001200002222101000021100211110220200122021201_3}
Это означает, что

,

,

,

,

,

.
При этом выполняются сравнения

,

,

,

.