Жесткость сооружений из палочек.

[amon]

Ехал из леса и задумался о простой задачке. Видимо, какой-то велосипед, но математического образования не хватает. Пусть у нас есть некоторое сооружение, составленное из $N$ палок заданной длины так, что палки соединены концами и могут как угодно крутиться относительно друг друга в точке соединения. В каких случаях такая конструкция окажется жесткой. Жесткость означает, что получившееся сооружение не может быть деформировано (нельзя изменить углы между ребрами).
Для ломаных на плоскости, вроде, все просто. В каждую вершину входит два ребра. Можно ввести начало координат в какой-нибудь вершине, написать систему уравнений и показать, что единственной жесткой ломаной, для которой такая система имеет (если имеет) единственное решение для косинуса угла между ребрами, является треугольник. А дальше, даже для плоскости, что-то ничего не придумывается, хотя вещь, вроде, простая, и должна быть решена лет 200 назад.

[dgwuqtj]

В пространстве есть изгибаемые многогранники.

[B@R5uk]

amon в сообщении #1716909 писал(а):

В каких случаях такая конструкция окажется жесткой.

Очень просто: число связей (то есть число палочек) должно покрыть число степеней свободы точек (концов палочек, которыми они соединяются) до такого предела, чтобы остались только степени свободы твёрдого тела. В пространстве размерности D у твёрдого тела D поступательных и R вращательных степеней свободы, где

$$R=\frac{D\bigl(D-1\bigr)}{2}$$

Для трёхмерного пространства это 3 поступательных и 3 вращательных степени свободы (всего 6), а для четырёхмерного — 4 и 6, соответственно (всего 10). Из числа вершин N, которые вы соединяете вашими палочками, помноженного на размерность пространства D, надо вычесть это суммарное число свобод, и получится требуемое число связей T:

$$T=DN-D-\frac{D\bigl(D-1\bigr)}{2}$$

Проблемы могут настать, когда некоторые связи являются выражаемыми через другие, зависимыми от других. Но чтобы это произошло надо обычно очень постараться.

А вообще, чтобы нужно получить жёсткую фигуру, то лучше ориентировать на симплексы. Это треугольники в плоскости и тетраэдры (не обязательно правильные) в пространстве. Построение тела начинается с треугольника/тетраэдра. Каждая новая точка должна соединяться с двумя (на плоскости) или тремя (в пространстве) другими точками, не лежащими на одной прямой (для пространства). Каждое такое соединение создаёт новый симплекс, который гарантирует неподвижность добавленной точки относительно остальных.

[amon]

B@R5uk в сообщении #1716913 писал(а):

А вообще, чтобы нужно получить жёсткую фигуру, то лучше ориентировать на симплексы.

Уже на плоскости есть жесткие фигуры, не разбиваемые на треугольники. Это я сообразил еще пока ехал. Поэтому простой подсчет числа степеней свободы не катит.

[B@R5uk]

amon в сообщении #1716914 писал(а):

есть жесткие фигуры, не разбиваемые на треугольники

А вы можете привести пример, пожалуйста? Что-то как-то так сходу и не соображу. Метод подсчёта свобод этому не препятствует, кстати. Симплексы гарантируют жёсткость простым инженерным подходом, это не значит, что других конструкций не может быть.

[dsge]

amon в сообщении #1716909 писал(а):

А дальше, даже для плоскости, что-то ничего не придумывается, хотя вещь, вроде, простая, и должна быть решена лет 200 назад.

Квадрат, прямоугольник нежестки, а равнобедренная (и не только) трапеция уже жесткая. В общем случае проблема вряд ли решена, где-то ...дцать лет тому назад народ пытался решить проблему методами алгебраической геометрии, бифуркациями и базисами Гребнера.

[B@R5uk]

dsge в сообщении #1716917 писал(а):

а равнобедренная трапеция уже жесткая.

Не, она не жёсткая. Так же как и у других четырёхугольников, у трапеции можно растягивать противоположные вершины (никто не запрещает сделать основания непараллельными). Чтобы эту степень свободы ликвидировать, надо добавить диагональное ребро. Как раз получится

$$2\cdot 4-2-1=5$$

То есть 8 степеней свободы у 4-х точек на плоскости ликвидируются 5-ю связями, после чего остаётся 3 степени свободы твёрдого тела.

[amon]

B@R5uk в сообщении #1716915 писал(а):

А вы можете привести пример.

$$\begin{tikzpicture} \draw (0,0) rectangle (1,1); \draw (0,0) -- (-1,0.5) --(0,1); \draw (0,0) -- (0.5,-1) -- (1,0); \draw (-1,0.5)--(0.5,-1); \end{tikzpicture}$$

[dsge]

B@R5uk в сообщении #1716919 писал(а):

Не, она не жёсткая.

Да, похоже, если не оставлять трапецию трапецией при деформации.

[amon]

dsge в сообщении #1716917 писал(а):

а равнобедренная (и не только) трапеция уже жесткая

У меня получается, что для графа с парными вершинами (два ребра в вершине) жесткий только треугольник. Для всего остального число переменных больше числа уравнений, хотя это еще не доказательство.

[B@R5uk]

amon, так это ж то, про что я толковал выше: три симплекса жёстко привязывают 5 точек друг к другу и 6-я привязана к двум другим двумя связями (или на это можно смотреть так: один стартовый симплекс, а остальные точки привязываются к нему одна за другой парами рёбер). Я думал про что-то вот в этом духе:

$$\begin{tikzpicture} \draw(0,1)--(0.78,0.62)--(0.97,-0.22)--(0.43,-0.9)--(-0.43,-0.9)--(-0.97,-0.22)--(-0.78,0.62)--(0,1); \draw(0.43,-0.9)--(0,1)--(-0.43,-0.9); \draw(0.78,0.62)--(-0.97,-0.22); \draw(-0.78,0.62)--(0.97,-0.22); \end{tikzpicture}$$

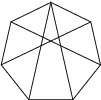
Я, правда, не уверен, что конкретно в этой изображённой фигуре нет одной степени свободы движений деформаций, связанной с тем, что одно из рёбер "лишнее", то есть набор связей вырожден.

-- 01.02.2026, 21:13 --

Вообще, на этот метод подсчёта свобод и связей можно навести математическую строгость. Запишем координаты всех соединяемых точек в столбец X, а все длины палочек — в столбец L. Получим многомерную нелинейную функцию:

$$L=L\bigl(X\bigr)\in\mathbb{R}^K,\qquad X\in\mathbb{R}^{DN}$$

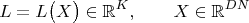
Сразу обратим внимание, что эта функция инвариантна относительно смещений точек в пространстве на общий вектор и относительно произвольного вращения всех точек как целого. Дифференциал вектора X есть инфинитезимальное движение точек, а дифференциал вектора L — соответствующее этому движению изменение длин палочек. Эти две величины связываются матрицей Якоби A частных производных функции L:

$$dL=A\;dX,\qquad A\in\mathbb{R}^{K\times(DN)},\qquad A_{ij}=\frac{dL_i}{dX_j}$$

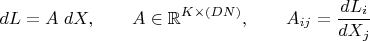
Фактически, мы линеаризовали задачу, и теперь вся мощь линейной алгебры на службе нашей цели. Воспользуемся этим.

Поскольку функция L инвариантна относительно указанных выше движений, соответствующие этим движениям дифференциалы (направления движений) будут гарантированно лежать в ядре линейного оператора, задаваемого матрицей A. То есть будет обязательно выполнено

$$A\;dX_T=0$$

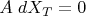
Неизменность длин палочек выражается просто:

$$dL=0$$

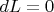
Получаем систему уравнений на возможные направления движений dX точек:

$$A\;dX=0$$

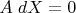
Мы уже знаем, что эта система будет иметь недоопределённость, связанную с природой связей в пространстве (соответствующей размерности). Но мы можем обеспечить линейную независимость строк этой системы, а так же их количество, чтобы гарантировать жёсткость тела при минимальном числе связей (одна строка — одна связь). Из соответствующего анализа ранга матрицы и её размеров и выходит правило подсчёта свобод и связей, что я привёл выше. А численный расчёт матрицы даёт практический способ проверить, что система связей действительно не вырождена (или вырождена, если такое желаемо).

[amon]

B@R5uk в сообщении #1716913 писал(а):

$$T=DN-D-\frac{D\bigl(D-1\bigr)}{2}$$

Контрпример. Согласно Вашей формуле устойчивость определяется только числом узлов и связей. Возьмем мою картинку и сделаем ее неустойчивой не меняя эти величины:

$$ \begin{tikzpicture} \draw (0,0) rectangle (1,1); \draw (0,0) -- (-1,0.5) --(0,1); \draw (0,0) -- (0.5,-1) -- (0,1); \draw (-1,0.5)--(0.5,-1); \end{tikzpicture}$$

[amon]

Есть подозрение (доказать не могу, но и контрпример не придумывается), что жесткость определяется топологией графа, соответствующего данной конструкции. Если это так, то соответствующий критерий можно искать, например, в свойствах матрицы смежности графов.

[mihaild]

Gemini нашло хорошую статью по теме - "The rigidity of graphs" (Asimow, Roth).
Ключевая теорема следующая. Пусть у нас есть граф с $v$ вершинами, $e$ ребрами, вложенный в $\mathbb R^n$. Edge function для этого графа $f: \mathbb R^{nv} \to \mathbb R^e$ - функция из вложений, $i$-я компонента которой равна длине $i$-го ребра.
Тогда во всех регулярных (в которых ранг $df$ максимально возможный) вложениях граф либо жесткий, либо нет, в зависимости от этого максимального ранга - если он равен $nv - (m + 1) \cdot (2n - m) / 2$, где $m$ - размерность подпространства, натянутого на вершины, то вложение жесткое, если меньше - то не жесткое.

Из этого следуют сложности с контрпримером к

amon в сообщении #1716946 писал(а):

жесткость определяется топологией графа, соответствующего данной конструкции

Авторы доказывают, что почти все вложения регулярны, соответственно либо почти все вложения жесткие, либо почти все не жесткие. Но есть примеры, когда часть вложений жесткие, часть - нет.

Вложение:

Screenshot_20260202_012544.png

Если сделать нижние ребра немного длиннее, то их станет возможным двигать. Если же они натянуты за счет двух треугольников - то нет.

[ozheredov]

mihaild
А как определяется не-жесткость? наличие $v$ бесконечно малых векторных перемещений в $R^n$, которые не все одновременно равны нулю и при этом длины рёбер сохраняются? А можно ли доказать, что все по разному вложенные в $R^n$ графы с одной и той же взвешенной матрицей смежности (вес = длина ребра) могут быть только либо одновременно жесткими, либо одновременно не-жесткими? (Жесткость не зависит от способа вложения.) Или это вообще не так?