По поводу "игры"
Ага, спасибо, в целом понятно. Мне кажется, это еще дополнительный уровень сложности, а разобраться бы с тем, что уже есть!

Мне удалось посчитать пять вилок, ими можно проколоть

клетку. Гарантии, что нельзя еще больше, - нету: использовал предположение из пары сообщений выше, что исходный "островок" из четырех проколотых клеток нужно наращивать чередуясь, то слева, то справа. Вот оно:
(71 прокол пятью вилками)
1, 4, 1, 7, 9, 1, 3, 1, 8, 2, 1, 7, 1, 5, 2, 1, 2, 1, 4, 5, 1, 2, 1, 2, 3, 1, 7, 1, 2, 6, 1, 4, 1, 8, 7, 1, 5, 1, 10, 3, 1, 8, 1, 9, 2, 1, 3, 1, 6, 2, 1, 2, 1, 5, 6, 1, 2, 1, 2, 10, 1, 3, 1, 2, 5, 1, 4, 1, 3, 10, 1
Это у меня считалось 45 минут на довольно приличном нотике; значит, шесть вилок на тех же мощностях - пара недель, эх.
Может быть можно что-то оптимизировать, как в идейном плане, так и в плане приемов программирования? Код немного так себе, но в принципе простой:
- fforkisl(k)={
- sb=4*(k^2+k+1);\\band size, hopefully enough
- B=vectorsmall(sb,i,0);
- bL=2*k^2+2*k+1; bR=bL+3;
- B[bL]=1; B[bL+2]=1;
- B[bR]=2; B[bR-2]=2;
- bL++; bR--;
-
- \\build initial 4-cell island
- i=1; s=1; lr=-1; d=6*i+2*s-3;
- B=vectorsmall(sb,x,if((x>bR||x<bL) & (B[x]==0) & (x%d==(bL-1)%d||x%d==(bL-1-lr*2*i)%d),1,B[x]));
-
- i=1; s=2; lr=1; d=6*i+2*s-3;
- B=vectorsmall(sb,x,if((x>bR||x<bL) & (B[x]==0) & (x%d==(bR+1)%d||x%d==(bR+1-lr*2*i)%d),2,B[x]));
-
- for(x=bR+1,sb,if(B[x]==0,bR=x-1;break));
- forstep(x=bL-1,1,-1,if(B[x]==0,bL=x+1;break));
-
- B0=B; bL0=bL; bR0=bR; mmax=0; Bmax=B;
-
- \\search through all combinations of forks and their tines
- for(lrc=0,2^(2*k-2)-1,
- lri=vectorsmall(2*k-2,i,2*(iferr(binary(lrc)[i],EE,0)-1/2));
-
- forperm(2*k-2,gi,
- B=B0; bL=bL0; bR=bR0;
- for(j=1,2*k-2,
- g=gi[j]+2; lr=lri[j];
- i=(g+1)\2; s=(g+1)%2+1; d=6*i+2*s-3;
-
- if(j%2==1, \\one shot left and one shot right of the island; strong assumption for the optimum strategy, valid for k=2,3,4
- B=vectorsmall(sb,x,if((x>bR||x<bL) & (B[x]==0) & (x%d==(bL-1)%d||x%d==(bL-1-lr*2*i)%d),g,B[x]))
- ,
- B=vectorsmall(sb,x,if((x>bR||x<bL) & (B[x]==0) & (x%d==(bR+1)%d||x%d==(bR+1-lr*2*i)%d),g,B[x]))
- ); \\if j
-
- \\calcualte new island bounds
- for(x=bR+1,sb,if(B[x]==0,bR=x-1;break));
- forstep(x=bL-1,1,-1,if(B[x]==0,bL=x+1;break));
-
- ); \\for j
-
- \\store the best result
- mcurr=bR-bL+1;
- if(mcurr>mmax,mmax=mcurr;Bmax=B);
-
- ); \\forperm
- ); \\for lrc
-
- print(mmax);
- print(Bmax);
- return([]);
- };
Работа все время вроде с небольшими объектами, просто это полный перебор довольно большого числа вариантов, а именно
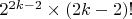
.
Ну и я каждый раз немного вздрагиваю, пиша конструкцию вида
B=vectorsmall(sb,x,if(...,g,B[x])), но вроде бы тормозить это не должно. Ее, видимо, стоило бы заменить на всякие
apply и
->, но я все никак не выучу этот пугающий синтаксис...