Задача про полоски с дырками

[anahronizm]

wrest в сообщении #1716295 писал(а):

Объясните что вы придумали, поточнее.

Постараюсь.
Ударили вилкой. Отступили вправо. Левый зуб вилки сделал 5 шагов - попадает на клетку номер 6. Тогда правый зуб попадёт на клетку номер 8.
Получается между правым зубом первого удара и левым зубом второго удара останется две не проколотые клетки.
Схема Х - прокол, О -целая клетка.
ХОХООХОХООХО - это для полоски 12.
Правый зуб третьего удара вышел за границу полоски - его не учитываем.
Спрашивайте - отвечу. Позже, а то руки в масле и начальник ругается, грозится выгнать уже.

[Ende]

Тема перемещена из форума «Олимпиадные задачи (М)» в форум «Помогите решить / разобраться (М)»
Причина переноса: топикстартер недопоставил задачу и сам не может ее решить.

[wrest]

anahronizm в сообщении #1716298 писал(а):

Схема Х - прокол, О -целая клетка.
ХОХООХОХООХО - это для полоски 12.

Ок, хорошо. Если первый (или какой-нибудь) удар левым зубом приходится на клетку $n$, то протыкаются клетки с номерами $k$ такими, что $k \equiv \{n,n+2\} \mod{5}$ -тут в фигурных скобках имеется в виду "или". То есть если первой вилкой мы тыкаем в первую клетку левым зубом, по проткнём клетки, номера которых дают остаток 1 или 3 при делении на 5, и это клетки 1,3,6,8,11,...

Теперь вторая вилка, если ею проткнуть первую клетку левым зубом, то какая будет схема?

[waxtep]

anahronizm в сообщении #1716288 писал(а):

Увы, я в математике почти ничего не понимаю.

Так а Вы попробуйте расшифровать мою нотацию, как я попытался Вашу, - только в обратную сторону. Вот, возьмем $k=1$, тогда $i=1,L=12$, - одна вилка, двенадцать клеток, пока совпадаем. Теперь возьмем $s_{11}=1$, тыкнем вилкой в первом проходе самую левую клетку. Получатся две прогрессии выколотых клеток с шагом $5$, у первой начальный член - $1$, а у второй - $3$; т.е. выколоты будут клетки $1,6,11$ и $3,8$. Пока тоже совпадаем. Второй проход (вилка та же, но интервалы между тыками ширше): возьмем самое левое не выколотое $s_{21}=2$ и получим две прогрессии с шагом $7$: $2,9$ и $6$. Всего за два прохода мы выкололи $7$ клеток из $12$: $1,2,3,6,8,9,11$. Теперь можете попробовать взять две вилки ($k=2, L=20,i=1,2$) и посмотреть, получается ли по моему описанию то, что Вы задумали.

anahronizm в сообщении #1716288 писал(а):

"... Какие из утверждений будут верны:
1. невозможно проколоть все клетки на любой полоске
2. начиная с некоторой полоски все последующие могут быть проколоты полностью
3. при любом увеличении полоски, среди полностью проколотых, найдётся такая, которую невозможно проколоть полностью."

Я голосую за вариант номер два (без доказательства). Наводящие соображения следующие: арифметическая прогрессия с шагом $d$ выкалывает из ряда последовательных натуральных чисел количеством $L$ не менее $\lfloor L/d \rfloor$ чисел, ну, натурально, "каждое $d$-ое" число она выкалывает. Если бы все выколотые числа были разными, то можно было бы сказать, что для данного $k$ будет выколото не менее

$$N_k=2\left(\sum_{i=1}^{k}{\left\lfloor\frac{L}{8i-3}\right\rfloor}+\sum_{i=1}^{k}{\left\lfloor\frac{L}{8i-1}}\right\rfloor\right)$$

чисел (это Вам придется или разобраться с моими обозначениями, или поверить). А эта штука при всех достаточно больших $k$ будет превышать $L$, потому что гармонический ряд логарифмически расходится (сумма обратных величин последовательных натуральных чисел от $1$ до $m$ растет как $\ln m$). И даже не надо двух проходов тыкания каждой вилкой, достаточно одного (только большее $k$ тогда понадобится).
Почему это не доказательство? Ну, потому что, как мы видели на примере полоски из $12$ клеток, иногда зубцы вилки в разных проходах (или зубцы разных вилок) тыкают в одну и ту же клетку; а, значит, последовательность $N_k$ растет не так быстро. Кажется, за счет свободы выбора аж $2k$ начальных позиций левого зубца, это можно победить. Строго доказать, наверное, не возьмусь (я тоже не математик)

[mihaild]

waxtep
Там вроде $6n \pm 1$ разность получается.
И соображения про плотность применять опасно. Например если натуральные числа можно покрыть прогрессиями с разностями $a_1 < a_2 < \ldots < a_k$, то хотя бы одно из $a_i$ делится либо на 2 либо на 3 https://arxiv.org/abs/1703.02133.

[waxtep]

mihaild в сообщении #1716332 писал(а):

waxtep
Там вроде $6n \pm 1$ разность получается.
И соображения про плотность применять опасно. Например если натуральные числа можно покрыть прогрессиями с разностями $a_1 < a_2 < \ldots < a_k$, то хотя бы одно из $a_i$ делится либо на 2 либо на 3 https://arxiv.org/abs/1703.02133.

Мне показалось, автор меряет "дырку" сантиметрами, а "интервал" - тетрадными клетками, т.е. полусантиметрами, я поэтому беру $8$ в качестве множителя. Типа, "дырка" $i$-ой вилки - $4i-2$, а "интервалы" в первом и втором проходе - $4i-2$ и $4i$ соответственно.

Вообще, есть смутное ощущение, что, под видом наивной задачки на раскрашивание клеток, нам подсунули нечто нетривиальное Балуюсь вручную (уже истыкал вилками всю скатерть), вплоть до $k=7$ включительно упорно остаются незакрашенными четыре клетки, при простой стратегии "тыкни сперва в самое левое невыколотое"

[waxtep]

Вроде, начиная с $k=12$ (полоска из сотни клеток) они опустошаются, в смысле, все точки выкалываются в итоге. Я не выдержал и написал предельно тупорыльную программу:

1. ffork(k)={ 
2. my(L=8*k+4,s=vector(L,i,i)); 
3. for(i=1,k, 
4. if(s==[],return(s)); 
5. s1=s[1]; 
6. d1=8*i-3; 
7. sex=vector((L-s1)\d1+1,ii,s1+(ii-1)*d1); 
8. s=setminus(s,sex); 
9. s1=s1+4*i-2; 
10. sex=vector((L-s1)\d1+1,ii,s1+(ii-1)*d1); 
11. s=setminus(s,sex); 
12. if(s==[],return(s)); 
13. s2=s[1]; 
14. d2=8*i-1; 
15. sex=vector((L-s2)\d2+1,ii,s2+(ii-1)*d2); 
16. s=setminus(s,sex); 
17. s2=s2+4*i; 
18. sex=vector((L-s2)\d2+1,ii,s2+(ii-1)*d2); 
19. s=setminus(s,sex); 
20. );\\for i 
21. return(s); 
22. }; 

[waxtep]

mihaild в сообщении #1716332 писал(а):

Там вроде $6n \pm 1$ разность получается.

У меня косяк в формуле для прогрессии "правого зубца при втором проходе"; и наверное Вы правы в определении шагов прогрессии, так текст автора тоже можно прочитать, и выглядит логичнее. Тогда вилка номер $i$ выкалывает при первом проходе точки $\{s_{1i}+(6i-1)m, s_{1i}+2i+(6i-1)m\}$, а при втором - $\{s_{2i}+(6i+1)m, s_{2i}+2i+(6i+1)m\}$. При таком подходе, программа считает, что все клетки можно выколоть начиная с $k=9$ (полоска из $76$ клеток). Это удивляет, т.к. $6i\pm1$ не делится ни на два, ни на три, но честно сказать, я не пытался пока вникнуть в приведенную Вами статью

-- 27.01.2026, 02:28 --

Последовательность выкалываний для $k=9,L=76$:

1. 1 1L 
2. [1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, 66, 71, 76] 
3. 1 1R 
4. [3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73] 
5. 1 2L 
6. [2, 9, 16, 23, 30, 37, 44, 51, 58, 65, 72] 
7. 1 2R 
8. [4, 11, 18, 25, 32, 39, 46, 53, 60, 67, 74] 
9. 2 1L 
10. [5, 16, 27, 38, 49, 60, 71] 
11. 2 1R 
12. [9, 20, 31, 42, 53, 64, 75] 
13. 2 2L 
14. [7, 20, 33, 46, 59, 72] 
15. 2 2R 
16. [11, 24, 37, 50, 63, 76] 
17. 3 1L 
18. [10, 27, 44, 61] 
19. 3 1R 
20. [16, 33, 50, 67] 
21. 3 2L 
22. [12, 31, 50, 69] 
23. 3 2R 
24. [18, 37, 56, 75] 
25. 4 1L 
26. [14, 37, 60] 
27. 4 1R 
28. [22, 45, 68] 
29. 4 2L 
30. [15, 40, 65] 
31. 4 2R 
32. [23, 48, 73] 
33. 5 1L 
34. [17, 46, 75] 
35. 5 1R 
36. [27, 56] 
37. 5 2L 
38. [19, 50] 
39. 5 2R 
40. [29, 60] 
41. 6 1L 
42. [34, 69] 
43. 6 1R 
44. [46] 
45. 6 2L 
46. [35, 72] 
47. 6 2R 
48. [47] 
49. 7 1L 
50. [52] 
51. 7 1R 
52. [66] 
53. 7 2L 
54. [54] 
55. 7 2R 
56. [68] 
57. 8 1L 
58. [55] 
59. 8 1R 
60. [71] 
61. 8 2L 
62. [57] 
63. 8 2R 
64. [73] 
65. 9 1L 
66. [62] 
67. 9 1R 
68. [] 
69. 9 2L 
70. [70] 
71. 9 2R 
72. [] 

[mihaild]

waxtep в сообщении #1716354 писал(а):

Это удивляет, т.к. $6i\pm1$ не делится ни на два, ни на три, но честно сказать, я не пытался пока вникнуть в приведенную Вами статью

Так у нас же две прогрессии для каждой разности.

[waxtep]

mihaild в сообщении #1716355 писал(а):

Так у нас же две прогрессии для каждой разности.

Значит, революция в арифметике отменяется, это приятно Спасибо!

PS: если оставить у вилки только один зубец и отменить второй проход (при этих условиях остается один набор прогрессий, как в статье), то для $k=17300,L=138404$ остаются невыколотыми $7520$ клеток, более 5%. В самом деле, все хорошо

PPS: нет, все же, тревожно: если у вилки один зубец, но второй проход есть, это ведь по одному экземпляру прогрессий с шагом $6i\pm1$. Программа считает, что при $k\geqslant74$ и при таких условиях можно выколоть все точки. Видимо, для разбора требуется свежая голова...

[anahronizm]

Извиняюсь, работал до позднего. Сейчас есть немного времени, чтоб ответить. Сначала изображу схему прокалываний.
здесь Х - прокол, О - целая клетка (ячейка).
Для бесконечной полоски:
Первая вилка с дыркой 1,
интервалом 2
ХОХООХОХООХОХООХОХООХОХООХОХООХОХООХОХООХОХООХОХ
здесь ХОХ - удар вилкой, у которой дырка =1, ОО - расстояние между ударами (интервал) =2
интервалом 4
ХОХООООХОХООООХОХООООХОХООООХОХООООХОХООООХОХОО
здесь ХОХ - удар вилкой, у которой дырка =1, ОООО - расстояние между ударами (интервал) =4

Вторая вилка с дыркой 3
интервалом 6
ХОООХООООООХОООХООООООХОООХООООООХОООХООООООХОООХООООООХОООХООООООХ
здесь ХОООХ - удар вилкой, у которой дырка=3, ОООООО - расстояние между ударами (интервал) =6
интервалом 8
ХОООХООООООООХОООХООООООООХОООХООООООООХОООХООООООООХОООХОООООООО
здесь ХОООХ - удар вилкой, дырка=3, ОООООООО - расстояние между ударами (интервал) =8

Третья вилка с дыркой 5
интервалом 10
ХОООООХООООООООООХОООООХООООООООООХОООООХООООООООООХОООООХООООООООООХ
здесь ХОООООХ - удар вилкой, дырка=5, ОООООООООО - расстояние между ударами (интервал) = 10
интервалом 12
ХОООООХООООООООООООХОООООХООООООООООООХОООООХООООООООООООХОООООХОООО
здесь ХОООООХ - удар вилкой, дырка=5, ОООООООООООО - расстояние между ударами (интервал)=12
И т.д.
Для каждой следующей вилки дырка увеличивается на +2, для каждой следующего прохода вилки расстояние между ударами увеличивается на +2
для наибольшего забивания ячеек можно сдвигать полностью эти схемы влево или вправо (т.е. делать первый удар вилкой в любом месте, а последующие - согласно данному интервалу)
Для первых двух вилок берётся полоска 12 ячеек. Для четырёх вилок берётся полоска 20 ячеек.
Последующие полоски увеличиваются на +8. Для каждой новой полоски добавляется два прохода новой вилки (с разными интервалами)
Если что-то не понятно, поясню позже.

-- 27.01.2026, 06:56 --

wrest в сообщении #1716295 писал(а):

Отвечаю:
1. Да
2. Нет
3. Да

Как я понимаю первый пункт противоречит третьему. Если "невозможно проколоть все клетки на любой полоске", то это противоречит фразе в третьем вопросе "среди полностью проколотых".
Каким будет верный ответ ?

-- 27.01.2026, 06:59 --

Ende в сообщении #1716299 писал(а):

Тема перемещена из форума «Олимпиадные задачи (М)» в форум «Помогите решить / разобраться (М)»
Причина переноса: топикстартер недопоставил задачу и сам не может ее решить.

Прекрасно, господин админ. Именно это я и просил сделать в моём первом сообщении: "Если я не верно оформил задачу или поместил её не в тот раздел, прошу подсказать или переместить."

-- 27.01.2026, 07:02 --

wrest в сообщении #1716326 писал(а):

то какая будет схема?

Теперь накидал схему. Если что-то не понятно - спрашивайте.

-- 27.01.2026, 07:10 --

waxtep в сообщении #1716328 писал(а):

Второй проход (вилка та же, но интервалы между тыками ширше): возьмем самое левое не выколотое $s_{21}=2$

При втором проходе первой вилки, если мы левым зубом выколем ячейку 2, то следующие выколотые будут 4, 9 и 11.

-- 27.01.2026, 07:13 --

waxtep в сообщении #1716336 писал(а):

истыкал вилками всю скатерть

Всю скатерть не надо. Длина полоски ограничена. Хотя, можно и всю скатерть, а потом просматривать определённой длины.

[anahronizm]

anahronizm в сообщении #1716359 писал(а):

Для первых двух вилок берётся полоска 12 ячеек. Для четырёх вилок берётся полоска 20 ячеек.
Последующие полоски увеличиваются на +8. Для каждой новой полоски добавляется два прохода новой вилки (с разными интервалами)

Блин, опять напутал.
Для первой вилки, для её двух проходов берётся полоска 12.
Для первой и второй вилки, когда каждая сделает два прохода берётся полоска 20 и т.д.
Извиняюсь, торопился.

[wrest]

waxtep в сообщении #1716354 писал(а):

Последовательность выкалываний для $k=9,L=76$:

Проверил несколько вилок, вроде прокалываете как надо.
Ещё интересно посмотреть сколько получается дырок, идущих подряд начиная с 1-й клетки, после каждого прохода.

[waxtep]

wrest, спасибо! Не могу процитировать Ваше сообщение, типовые проблемы с обрезанием страницы. Удобнее выдавать количество идущих подряд дырок перед проходом, что то же самое, как и после предыдущего прохода, конечно; добавил, для 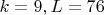$k=9,L=76$ выглядит так:

1. 1 1L 0 [1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, 66, 71, 76] 
2. 1 1R 1 [3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73] 
3. 1 2L 1 [2, 9, 16, 23, 30, 37, 44, 51, 58, 65, 72] 
4. 1 2R 3 [4, 11, 18, 25, 32, 39, 46, 53, 60, 67, 74] 
5. 2 1L 4 [5, 16, 27, 38, 49, 60, 71] 
6. 2 1R 6 [9, 20, 31, 42, 53, 64, 75] 
7. 2 2L 6 [7, 20, 33, 46, 59, 72] 
8. 2 2R 9 [11, 24, 37, 50, 63, 76] 
9. 3 1L 9 [10, 27, 44, 61] 
10. 3 1R 11 [16, 33, 50, 67] 
11. 3 2L 11 [12, 31, 50, 69] 
12. 3 2R 13 [18, 37, 56, 75] 
13. 4 1L 13 [14, 37, 60] 
14. 4 1R 14 [22, 45, 68] 
15. 4 2L 14 [15, 40, 65] 
16. 4 2R 16 [23, 48, 73] 
17. 5 1L 16 [17, 46, 75] 
18. 5 1R 18 [27, 56] 
19. 5 2L 18 [19, 50] 
20. 5 2R 28 [29, 60] 
21. 6 1L 33 [34, 69] 
22. 6 1R 34 [46] 
23. 6 2L 34 [35, 72] 
24. 6 2R 46 [47] 
25. 7 1L 51 [52] 
26. 7 1R 53 [66] 
27. 7 2L 53 [54] 
28. 7 2R 54 [68] 
29. 8 1L 54 [55] 
30. 8 1R 56 [71] 
31. 8 2L 56 [57] 
32. 8 2R 61 [73] 
33. 9 1L 61 [62] 
34. 9 1R 69 [] 
35. 9 2L 69 [70] 

Код:

1. ffork(k)={ 
2. my(L=8*k+4,s=vector(L,i,i)); 
3. for(i=1,k, 
4. if(s==[],return(s)); 
5. s1=s[1]; 
6. d1=6*i-1; 
7. sex=vector((L-s1)\d1+1,ii,s1+(ii-1)*d1); 
8. print(i," 1L ",s1-1," ",sex); 
9. s=setminus(s,sex); 
10.  
11. if(s==[],return(s)); 
12. smin=s[1]; 
13. s1=s1+2*i; 
14. sex=vector((L-s1)\d1+1,ii,s1+(ii-1)*d1); 
15. print(i," 1R ",smin-1," ",sex); 
16. s=setminus(s,sex); 
17.  
18. if(s==[],return(s)); 
19. s2=s[1]; 
20. d2=6*i+1; 
21. sex=vector((L-s2)\d2+1,ii,s2+(ii-1)*d2); 
22. print(i," 2L ",s2-1," ",sex); 
23. s=setminus(s,sex); 
24.  
25. if(s==[],return(s)); 
26. smin=s[1]; 
27. s2=s2+2*i; 
28. sex=vector((L-s2)\d2+1,ii,s2+(ii-1)*d2); 
29. print(i," 2R ",smin-1," ",sex); 
30. s=setminus(s,sex); 
31.  
32. );\\for i 
33. return(s); 
34. }; 

[mihaild]

waxtep в сообщении #1716356 писал(а):

Программа считает, что при $k\geqslant74$ и при таких условиях можно выколоть все точки

А покажите координаты первого прокола.
$k$ - это число вилок (соответствено у последней прогрессии шаг $445$) или проходов (соответственно у последней шаг $223$)?
Я доказательство в статье особо не смотрел. Вроде бы выглядит нетривиальным, но подъемным.