придется вычислить все проколотые разными вилками клетки, и сказать, что "а не проколотые - это все остальные".
Это немного скучно...
Я придумал способ описания всех не проколотых клеток. Кривенько, косенько, но в виде формулы. Наверное, математики и так это знают, но попробую рассказать, чего я наворотил.
Для этого сначала нужно озвучить более простую задачу:
Задача про плохих стрелковДва стрелка стреляют одновременно по одному ряду мишеней. Начинают оба с первой, крайней левой мишени. Целятся, стреляют. Независимо от результата, целятся и стреляют в следующую мишень, которая расположена правее. Вот только стреляют плохо: первый стрелок попадает только в каждую (a)-тую мишень, второй только в каждую (b)-тую мишень. Стрельба прекращается, когда оба стрелка попадут в одну и ту же мишень.
Требуется найти способ описания номеров тех мишеней, в которые не попал ни один стрелок. Известно, что а не равно b и они взаимно простые.
Возможно ли решение записать в виде некоего выражения (функции) ?
Например: первый попадает только в каждую 4-ю мишень, второй в каждую 5-ю. Стрельба прекратится на 20-й мишени, в которую попадут оба. Как можно описать номера
1,2,3,6,7,9,11,13,14,17,18,19 - по этим мишеням промахнулись оба стрелка ?
Намного ли усложнится задача, если стрелков будет 3, 4, 5 или...немного больше ?
Представьте, что при попадании в одну мишень одновременно, стрелки продолжают стрелять по мишеням дальше. Можно ли описать все мишени, по которым не попал ни один из стрелков ?
Да, можно записать выражение, которое описывает номера всех мишеней, в которые не попал ни один из стрелков, если представить, что ряд мишеней бесконечен.
Но для этого я рассмотрел вариант ещё проще, когда стрелок только один и он, например, попадает только в каждую пятую мишень. Конечно, легко описать все мишени, в которые он попал как 5х.
А вот как описать мишени под номером 1,2,3,4 ?
Для этого я ввёл понятие интервальной переменной

которая принимает целые значения от 1 до i.
Тогда все мишени, в которые не попал стрелок можно описать как
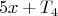
где х принимает целые значения
Как-то плохо я понимаю, как тут оформляются формулы...
-- 01.03.2026, 11:18 --Или в общем виде:
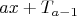 -- 01.03.2026, 11:49 --
-- 01.03.2026, 11:49 --А если стреляют два стрелка, как в задаче про плохих стрелков? Т.е. первый попадает в каждую четвёртую мишень, второй попадает в каждую пятую мишень. Как описать те мишени, в которые не попал ни один из стрелков ?
Для этого можно использовать формулу:
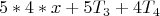
Или в общем виде, чтобы было более понятно (если первый стрелок попадает только в каждую а-тую мишень, а второй стрелок в каждую b-тую мишень):
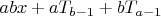
Если же стрелков будет трое, и каждый из них попадает только в каждую a-тую,b-тую, с-тую мишень соответственно, то все не пробитые мишени можно описать так:
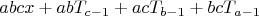
Эту формулу можно расширить на любое количество стрелков.
Так же можно описать номера тех мишеней, в которые не попал ни один из двух стрелков, если один попадает только в каждую, например, 5x+1 мишень, а второй только в каждую 7х+2 мишень.
Тогда формула будет выглядеть так:
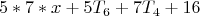
Где 16 – значение левой или правой части диофантова уравнения 5x+1=7у+2 при верном его решении.
можно обратить внимание, что рисунок распределения мишеней при этом не изменился, а только сдвинулся.
Вообще, если первый стрелок попадает только в каждую ax+

мишень, а второй в каждую bx+

мишень, то в общем виде эту формулу можно записать так:
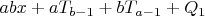
где

- значение левой или правой части диофантова уравнения ax+

= bу+

при верном его решении.
Аналогично записывается формула для трёх стрелков:
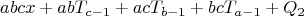
где

-значение левой или правой части диофантова уравнения abx+

= сx+

при верном его решении, если третий стрелок попадает только в каждую сx+

мишень.
Наверное, будет своевременно пояснить, что в этих задачах мы имеем дело с пересечением множеств определенного вида – для удобства назову их множествами с интервальной переменной.
Немного позже продолжу - времени не хватает.