Задача про полоски с дырками

[wrest]

waxtep в сообщении #1717370 писал(а):

но так (построением на полоске общего периода), кажется, долговато считать.

Если я правильно улавливаю ход мысли, то так вообще не посчитать в случае не взаимно простых периодов (привет от КТО), а это начинается уже с третьей вилки.

[wrest]

waxtep в сообщении #1717370 писал(а):

Сейчас, благодаря помощи Dmitriy40 и Вашей, wrest, пять вилок считаются за шесть минут, а для шести оценка в двое суток.

Да, я сдавал ваш код отсюда post1717187.html#p1717187 Qwen-у и оно сказало, что на пару порядков скорость можно улучшить сходу. Но диалог потерялся потом (то ли я не залогинен был то ли ещё что). Там у Qwen вроде ещё какие-то идеи были типа мемоизации и может ещё на несколько порядков но это не точно

[waxtep]

wrest в сообщении #1717388 писал(а):

Если я правильно улавливаю ход мысли, то так вообще не посчитать в случае не взаимно простых периодов (привет от КТО), а это начинается уже с третьей вилки.

С четвертой, ага, там период второго прохода $25$ кратен периоду самого первого $5$. Там можно несколько более коротких полосок рассмотреть:

waxtep в сообщении #1716779 писал(а):

Ну да, для четырёх вилок прогрессии с взаимнопростыми периодами, кроме периода $5$ можно сложить в произвольную кучу, любая комбинация на общем периоде встретится. А потом наложить прогрессию с периодом $5$ в пяти возможных положениях (в силу симметрии задачи достаточно в трех). Это можно аккуратно обобщить на случай любых не взаимнопростых периодов

wrest в сообщении #1717393 писал(а):

Да, я сдавал ваш код отсюда post1717187.html#p1717187 Qwen-у и оно сказало, что на пару порядков скорость можно улучшить сходу. Но диалог потерялся потом (то ли я не залогинен был то ли ещё что). Там у Qwen вроде ещё какие-то идеи были типа мемоизации и может ещё на несколько порядков но это не точно

Ага, а потом оно скажет, что этот кусок хинди-кода обещает революцию в математике, програзме и животноводстве, и лучше бы припрятать его хорошенько от спецслужб, не забыв написать в нобелевский комитет... Людям доверяю больше! Реально Вам с Дмитрием спасибо, - я бы не стал искать баги и новые идеи до оптимизации, все таки считать днями и годами, - не мое. Несколько часов, туда-сюда.

Тем временем $M(6)\geqslant126$ и оно еще считает; похоже, эта штука растет супер-квадратично, быстрее параболы.

[wrest]

waxtep в сообщении #1717397 писал(а):

Ага, а потом оно скажет, что этот кусок хинди-кода обещает революцию в математике, програзме и животноводстве, и лучше бы припрятать его хорошенько от спецслужб,

Нене, идеи у ИИ были весьма здравые. Оценка (без сильной переработки) там была ~200 раз, что у вас и получилось. Но есть и тонкости именно в pari/gp относящиеся к тому, что иногда логически тот же код начинает работать сильно быстрее если внести логику внутрь функций создания векторов и т.п. Я как раз и ждал что вы обратитесь за оптимизацией вашего кода (как индикатор, что интерес ещё не потерян).

-- 06.02.2026, 12:32 --

waxtep в сообщении #1717397 писал(а):

Тем временем $M(6)\geqslant126$ и оно еще считает; похоже, эта штука растет супер-квадратично,

Ну с учётом того, что начиная с какой-то вилки по всей видимости будет $M(n)=\infty$ то есть все натруальные покроются целиком, это и неудивительно. А может и не покроются

[waxtep]

wrest в сообщении #1717410 писал(а):

Нене, идеи у ИИ были весьма здравые. Оценка (без сильной переработки) там была ~200 раз, что у вас и получилось. Но есть и тонкости именно в pari/gp относящиеся к тому, что иногда логически тот же код начинает работать сильно быстрее если внести логику внутрь функций создания векторов и т.п. Я как раз и ждал что вы обратитесь за оптимизацией вашего кода (как индикатор, что интерес ещё не потерян).

А, понял, спасибо. Но 200 я пока не выжал, лишь ~10, есть еще значит потенциал для оптимизации. В примерно 500 раз быстрее оно теперь считает по сравнению с другой программой, которая дает гарантированный максимум, перебирая весь общий период (с учетом тонкостей, когда периоды не взаимнопросты). Текущая программа такой гарантии не дает: она по сути преследует сильно модифицированную наивную стратегию:
1. Как и в ней, в очередном проходе тыкаем в первую непроколотую клетку;
2. Но делаем это строго то слева от уже проколотого диапазона, то справа (именно это дает ускорение; стратегии с несбалансированным ростом влево/вправо не рассматриваются);
3. И не берем для очередного прохода обязательно младшие доступные вилку и проход и левый зубец, а перебираем все возможные варианты вилка-проход-зубец.

Интерес же во мне эта задача пробудила буйный понятно, что без гарантии какого-либо результата, но ведь "пусть он проиграл, но занимался же делом достойным", не дословно из многих античных авторов; у них, как правило, "погиб" и т.п.

wrest в сообщении #1717410 писал(а):

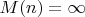
Ну с учётом того, что начиная с какой-то вилки по всей видимости будет $M(n)=\infty$ то есть все натруальные покроются целиком, это и неудивительно. А может и не покроются

anahronizm в сообщении #1717195 писал(а):

Думаю, всё это безобразие можно выразить формулами, но я их не знаю.

Да, вот это вопросы на миллион или на сто рублей по крайней мере.

Вот пока наилучшее для шести вилок, $126$ проколотых клеток подряд:

1. Вилка, i; Проход, s; Дырка, h=2i-1; Интервал, p=4i+2s-4; Период, d=6i+2s-3 
2.  
3. i    s    зубец          тык          h    p     d 
4. ============================= 
5. 1    1    левый        x             1    2     5 
6. 1    2    правый      x+3         1    4     7 
7. 3    1    левый        слева      5    10   17 
8. 2    1    левый        справа    3    6     11 
9. 2    2    левый        слева      3    8     13 
10. 6    2    левый        справа    11  24    37 
11. 6    1    правый      слева      11  22    35 
12. 4    2    правый      справа    7    16    25 
13. 3    2    правый      слева      5    12    19 
14. 5    2    левый        справа    9    20    31 
15. 5    1    левый        слева      9    18    29 
16. 4    1    левый        справа    7    14    23 

[anahronizm]

wrest в сообщении #1717410 писал(а):

Ну с учётом того, что начиная с какой-то вилки по всей видимости будет $M(n)=\infty$ то есть все натруальные покроются целиком, это и неудивительно.

Не покроются. Никогда. Если мы будем сохранять конфигурацию вилок по условию задачи, и проходы, то никогда невозможно будет обеспечить забитие бесконечной полоски, сколько бы вилок мы ни взяли.
Мало того, рисунок забития вилками на бесконечной полоске всегда будет обладать периодичностью и зеркальной симметрией внутри периода. И даже если мы будем пытаться сдвигать удары вилок, то на бесконечной полоске общий рисунок не изменится, но будет сдвинут.

[wrest]

anahronizm в сообщении #1717497 писал(а):

Не покроются. Никогда.

Ок, как скажете

[mihaild]

anahronizm в сообщении #1717497 писал(а):

Если мы будем сохранять конфигурацию вилок по условию задачи, и проходы, то никогда невозможно будет обеспечить забитие бесконечной полоски, сколько бы вилок мы ни взяли.

Вы умеете это доказывать?

[waxtep]

Если наблюдать за динамикой роста непрерывно проколотой полосы, то вот, -
1. повсюду образуются небольшие островки из двух, трех, четырех проколов подряд;
2. некоторые из них медленно растут на одну-две клетки в очередном проходе;
3. и довольно часто в каждом проходе мелкие островки сливаются в более крупные, за счет прокола единственной разделяющей их клетки. Иногда в один остров сливаются не два, а три-четыре острова вместе за один проход. На картинке для шести вилок это наблюдается уже довольно выраженно.

И тогда размер максимальной проколотой полоски должен быть по идее похож на экспоненту, за счет такого лавинного объединения островков. Эксель для трех-шести вилок предлагает $\tilde M(k)=4,5355\exp{(0,5524k)}$, в принципе, хорошо ложится (одна-две вилки - ожидаемо плохо, потому исключил; надо бы больше точек, да где же их взять ):

$$\begin{tabular}{c|c|c|c|c|}$ k $ & 3 & 4 & 5 & 6\\ \hline $ M(k) $ & 24 & 41 & 71^{+} & 126^{+}\\ $ \tilde{M}(k) $ & 23,8 & 41,3 & 71,8 & 124,8\end{tabular}$$

Экспонента... она мощная, может и весь $\mathbb{N}$ внезапно покрыть, после какого-то $k$.
Ну это все тоже конечно, "отдельные соображения".

[anahronizm]

mihaild в сообщении #1717527 писал(а):

Вы умеете это доказывать?

Нет, нет, доказывать я это не умею. Впрочем, я не умею доказывать сколько будет дважды два. Если только на пальцах.
Да и был уверен, что это и так известно математикам. Впрочем, можете обозвать гипотезой и подписать моим именем.
Так вот, на периоде всегда будут существовать группы из одного или двух элементов, которые не будут проколоты. И таких групп при росте количества вилок (период тоже растёт) в периоде будет только увеличиваться. И количество данных групп можно выразить формулой (это снова гипотеза).
Эх, понесло меня на гипотезы...
Вот ещё одна: максимальный размер полоски, которую можно забить вилками также можно выразить формулой.
Ну, ладно, ещё один секрет-гипотеза: номера непробитых клеток тоже можно выразить формулой. Причём, общей формулой, которая учитывает количество вилок, размер дырок и интервалов и даже размер сдвига (ну, когда мы пытаемся начать новый проход вилкой, мы можем начать с произвольного места - это и будет сдвиг).

[waxtep]

Гипотезы - это хорошо!

anahronizm в сообщении #1717545 писал(а):

Так вот, на периоде всегда будут существовать группы из одного или двух элементов, которые не будут проколоты. И таких групп при росте количества вилок (период тоже растёт) в периоде будет только увеличиваться.

Я, честно скажу, не знаю, к чему склониться, покроет когда-либо весь период или нет. И рост периода, и рост суммарного размера "жирных" островков, видимо, имеют сходный характер. Forse si, forse no

Да, должен ответственно заявить: проверил вручную возможность прокола $126$ клеток подряд шестью вилками. В любой программе ведь есть баги... Картинка: https://disk.yandex.ru/i/JbCLERptsVsNAw (до хостингов картинок что-то не могу достучаться). Оранжевые треугольники - моменты объединения трех островков (на самом деле, четырех; четвертый в обоих случаях просто сравнительно мелкий, не стал отмечать его). Что еще сказать; на исследуемой полоске из $320$ клеток (на картинке показано меньше) включая $126$ проколотых, всего не проколото $34$ клетки, около 11%.

[anahronizm]

mihaild в сообщении #1717527 писал(а):

Вы умеете это доказывать?

Увы, я и правда не умею доказывать. Даже не представляю, что нужно написать, чтобы это являлось доказательством.
А вот формула, которая которая учитывает количество вилок, размер дырок и интервалов и даже размер сдвига, будет являться доказательством? Или нет, даже если все результаты, вычисленные с её помощью верны?
Да, кажется, если мы будем брать вилки и проходы, как указаны в задаче, то групп из двух, подряд идущих не проколотых клеток на периоде (если рассматривать бесконечную полоску) будет всегда нечётное количество.
Но такое разбиение всегда будет обладать зеркальной симметрией, значит, одна такая группа всегда будет находиться в середине периода.
Для уточнения: за начало периода нужно принять ту клетку(точку), куда попадёт левый зубец каждой вилки.

[anahronizm]

Я вот что думаю: сама формула для вычисления не может считаться доказательством. Формула должна основываться на выводах и являться их подтверждением.
Даже если записать полную формулу, которая будет давать верный результат при вычислении, нет доказательств того, что она ВСЕГДА даст верный результат.
Тут я правильно рассуждаю?
Ну, а если с другой стороны: пусть у нас нет доказательств, но есть рабочая формула, можно ли всегда полагаться на её результаты? Или, как в данном случае, есть данные компьютерной программы, можем ли мы опираться на них при формулировке выводов? Или такие данные дают только направления для исследований ?

[mihaild]

anahronizm в сообщении #1717606 писал(а):

Увы, я и правда не умею доказывать

Тогда не надо делат такие категоричные утверждения как

anahronizm в сообщении #1717497 писал(а):

Не покроются. Никогда. Если мы будем сохранять конфигурацию вилок по условию задачи, и проходы, то никогда невозможно будет обеспечить забитие бесконечной полоски, сколько бы вилок мы ни взяли.

Ничего магического в выражении "формулами" нет. Любой алгоритм можно в некотором разумном смысле записать формулой. Но отвечать на какие-то содержательные вопросы - это ничем не поможет.
Написать программу, проверяющую, можно ли покрыть полоску данной длины (или даже можно ли покрыть все натуральные числа) - можно, и waxtep это уже сделал. Верить её результатам можно. Но считает она долго, для 10 вилок мы таким методом не посчитаем ничего за срок жизни вселенной. Можно ли сильно быстрее - не знаю.

Может быть для конкретно такой конфигурации вилок есть какое-то простое решение, которого я не вижу. В общем случае - это всё открытые вопросы, и даже чтобы прикинуть, что из этого может оказаться подъемным, а что нет - нужен не просто математик, а специалист конкретно по ТЧ.

[anahronizm]

mihaild в сообщении #1717812 писал(а):

Тогда не надо делат такие категоричные утверждения

Да что с меня взять? Я ж не математик, поэтому мне можно.
Да и в утверждениях, вроде, нигде не ошибся. Думаю, waxtep и wrest даже смогут подтвердить верность таких утверждений. Хотя, про "...то групп из двух, подряд идущих не проколотых клеток на периоде (если рассматривать бесконечную полоску) будет всегда нечётное количество..." могу и ошибиться - это уже на интуиции, я не вдавался сильно в этот вопрос.
Думаю, пока гайки кручу да тормоза прокачиваю.