test
благодарю за беседу
И Вам спасибо.
(при

)
У нас p

transcendent, Вы доказали, что
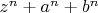
- целое. И с этим глупо было бы спорить, сумма целых чисел в натуральных степенях, - конечно, это целое. Но Вам для получения желаемого противоречия надо доказать целость
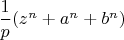
, чего Вы не сможете сделать никогда (при

), потому что по условию

не делит

. Вы, по сути, вводите это как дополнительное (ложное) утверждение, и тогда получаете противоречие. Ну, "из лжи следует что угодно", так работает математическая логика; но доказательством рассуждение, содержащее ложную посылку, служить не может. Мне к этому нечего добавить, благодарю за беседу.
Позже об этом.
(Оффтоп)
Ладно, с этим процитированным постом попробуем разобраться позже, если потребуется даже после нынешнего комментария с примерами и "третьей причиной". Раз товарищу даже мастиыте математики-не указ, что ту ещё скажешь? Да...Он, конечно, скажет "не надо прятаться за спинами великих людей, Вы сами докажите , что

чёрным по белому". А чего я должен это доказывать, если это общепринятое неотъемлемое математическое правило? На чём-то же надо стоять... Пока ничего в ответ на это не могу сказать.Честно.

Ладно, потому попробую поанализировать цитату.
Спасибо, людям, которые изобрели отрицательные числа!
(Оффтоп)
У меня нет сомнений в квалификации оппонента(правильно подобрал термин?-да я и права такого здесь не имею высказывать сомнения письменно, даже, если бы они и были. Одно хорошо, что кто-то нашёлся поговорить со мной здесь.)-я уверен, что он знает, что П. Ферма тоже знал про отрицательные числа.
Если предположить существование натуральных

,

,

в уравнении Ферма с нечётными степенями n

, это будет означать, что есть целые

,

,

. И, следовательно, если есть целое
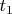
, то всегда ему найдётся и целое

.
(Оффтоп)
Собственно, на этом всё. Не знаю-чего тут непонятного? Зачем огород лишний ещё городить?
Пусть имеем следующее выражение, записанное в десятичной системе счисления:
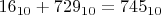
, (1). Допустим, что надо записать это выражение в системе счисления с основанием 31. И мы все договорились, что буквы от A до U английского алфавита мы будем использовать в качестве цифр так, что буква

это число

в десятичной системе счисления и т.д., включая
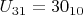
. Чтобы легчу возможному читателю знать, что есть что, не залезая на другие страницы в поисках английских букв, давайте выпишем все эти буквы уже в качестве цифр системы счисления с основанием

и указанием справа-какому числу десятичной системы счисления есть соответствие:

,
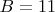
,

,
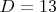
,
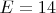
,
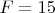
,
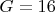
,
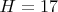
,
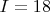
,

,

,
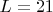
,
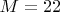
,
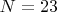
,
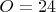
,
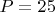
,
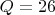
,
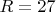
,

,
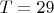
,
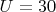
.
Выражение (1) в системе счисления с основанием

(далее, для простоты, индексы писать не будем, а уравнение записано, как текст, поскольку система его не пропускает почему-то, и даже, если индексы добавить по правилам):
G+NG=O1, (2).
Для выражения (2) есть следующие 31-адические кубические корни:
x_{2.1}=...G8I8 или в канонической записи
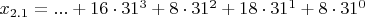
,
x_{2.2}=...LPH9 или в канонической записи
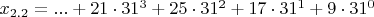
,
x_{2.3}=...NRQE или в канонической записи
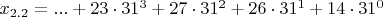
,
y_{2.1}=...DRR8 или в канонической записи
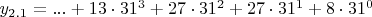
,
y_{2.2}=...(0)9 или в канонической записи
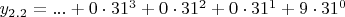
,
y_{2.3}=...H33E или в канонической записи
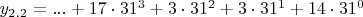
,
z_{2.1}=...5GSUP или в канонической записи
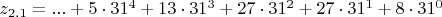
,
z_{2.2}=...A3N5 или в канонической записи
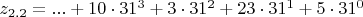
,
z_{2.3}=...3T81 или в канонической записи
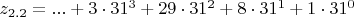
.
Умножив выражение на

, мы получаем другое выражение, которое запишем в

-адической форме:
...(U)F+...(U)7E=...(U)6U, (3), котрое тоже имеет соответствующие кубические корни и они представлены в этом списке:
x_{3.1}=...EMCN или в канонической записи
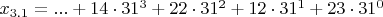
,
x_{3.2}=...95DM или в канонической записи
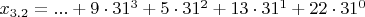
,
x_{3.3}=...734H или в канонической записи
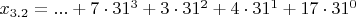
,
y_{3.1}=...H33N или в канонической записи
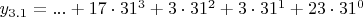
,
y_{3.2}=...(U)M или в канонической записи
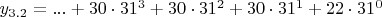
,
y_{3.3}=...DRRH или в канонической записи
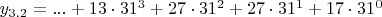
,
z_{3.1}=...PE206 или в канонической записи
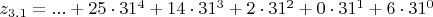
,
z_{3.2}=...KR7Q или в канонической записи
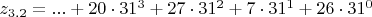
,
z_{3.3}=...R1MU или в канонической записи
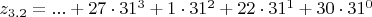
.
Нетрудно убедиться, что если складывать соответствующие корни выражений (

) и (

), то

будет получаться.
Например, любой может сделать проверку для сложения корней

с соответствующими индексами. Например, 2.1 и 3.1; 2.2 и 3.2 и т.д.
Вывод: Вопросы по целости параметра  разрешимы в пользу признания этого факта не только по причинам, приведённым выше, но и, поскольку, они касаются целых чисел в степенях,
разрешимы в пользу признания этого факта не только по причинам, приведённым выше, но и, поскольку, они касаются целых чисел в степенях,  , которые являются целыми заведомо и в любом случае, а не гипотетических чисел
, которые являются целыми заведомо и в любом случае, а не гипотетических чисел  : сложение
: сложение  и -
и - , естественно, даёт
, естественно, даёт  .
.