Гипотеза о симметричных простых близнецах

[Dmitriy40]

Ryzl в сообщении #1707135 писал(а):

Вероятность, что два числа, расположенные симметрично относительно $N/2$, одновременно простые:

$ p = \rho^2 = \left(\frac{1}{\ln (N/2)}\right)^2 $.

Это верно только для чисел прямо около $N/2$. Для чисел далеко от $N/2$ (например если меньшее простое меньше $10^4$ как это и есть для $N<4\cdot10^{18}$) это уже неверно. Надо брать именно произведение двух логарифмов с разными аргументами, а не квадрат одного. То есть более правильное левое не равно вашему правому:
$\rho(N,p)=\frac{1}{\ln(p)\ln(N-p)} \ne \frac{1}{\ln^2(N/2)}$

И потом ниже не просто умножать на $N/2$, а честно суммировать по всем натуральным до $N/2$, беря под суммой произведение двух логарифмов от разных аргументов.

Другое дело что левую формулу вполне можно аппроскимировать (или ограничить сверху) например правой. Но это надо проговаривать прямо! И обосновывать что да, можно. Иначе это всего лишь грубая оценка.

Ryzl в сообщении #1707135 писал(а):

Вывод
Вероятность отсутствия пар симметричных простых чисел на одинаковом расстоянии от $N/2$ при больших $N$ практически равна нулю, т.е. такие пары встречаются практически наверняка.

Вывод однако верный.
С ним кстати никто и не спорил.
Только это не доказательство что вероятность равна нулю строго. Она ему равна "практически", а не строго, как утверждается в бинарной гипотезе Гольдбаха.

[Ryzl]

пианист в сообщении #1707144 писал(а):

Даже если считать, что применение методов ТВ в данном случае сколько-то правомерно (вообще-то я согласен с мнением уважаемого mihaild по данному вопросу), откуда Вы так-таки знаете, что эти "события" независимы?

Вы предлагаете считать вхождение простых чисел не независимыми событиями? Т.е. вхождение каждого простого числа зависит от других?

-- 25.10.2025, 20:04 --

Dmitriy40 в сообщении #1707146 писал(а):

Ryzl в сообщении #1707135 писал(а):

Вероятность, что два числа, расположенные симметрично относительно $N/2$, одновременно простые:

$ p = \rho^2 = \left(\frac{1}{\ln (N/2)}\right)^2 $.

Это верно только для чисел прямо около $N/2$. Для чисел далеко от $N/2$ (например если меньшее простое меньше $10^4$ как это и есть для $N<4\cdot10^{18}$) это уже неверно. Надо брать именно произведение двух логарифмов с разными аргументами, а не квадрат одного. То есть более правильное левое не равно вашему правому:
$\rho(N,p)=\frac{1}{\ln(p)\ln(N-p)} \ne \frac{1}{\ln^2(N/2)}$

И потом ниже не просто умножать на $N/2$, а честно суммировать по всем натуральным до $N/2$, беря под суммой произведение двух логарифмов от разных аргументов.

Другое дело что левую формулу вполне можно аппроскимировать (или ограничить сверху) например правой. Но это надо проговаривать прямо! И обосновывать что да, можно. Иначе это всего лишь грубая оценка.

Ryzl в сообщении #1707135 писал(а):

Вывод
Вероятность отсутствия пар симметричных простых чисел на одинаковом расстоянии от $N/2$ при больших $N$ практически равна нулю, т.е. такие пары встречаются практически наверняка.

Вывод однако верный.
С ним кстати никто и не спорил.
Только это не доказательство что вероятность равна нулю строго. Она ему равна "практически", а не строго, как утверждается в бинарной гипотезе Гольдбаха.

Я и не говорю (хотя надеялся) что это доказательство гипотезы Гольдбаха, но это обоснование бессмысленности поиска таких четных чисел у которых не будет пар простых чисел дающих в сумме данное четное число. Экономия электроэнергии однако ))

[Dmitriy40]

Ryzl в сообщении #1707150 писал(а):

Вы предлагаете считать вхождение простых чисел не независимыми событиями? Т.е. вхождение каждого простого числа зависит от других?

Вообще говоря - да. Если число $p>3$ простое, то оба числа $p-1,p+1$ абсолютно точно составные и простыми быть никак не могут и значит вероятность для них вовсе не $1/\ln(x)$, а точно $0$.
Потому та оценка через обратных логарифм верна лишь в среднем, для очень больших чисел и интервалов, и чем больше, тем точнее.

Ryzl в сообщении #1707150 писал(а):

но это обоснование бессмысленности поиска таких четных чисел у которых не будет пар простых чисел дающих в сумме данное четное число. Экономия электроэнергии однако ))

И тоже нет. Даже если плюнуть на ошибки и скорректировать на много порядков, она хоть и останется чрезвычайно малой, но всё равно не нулевой и может случиться. Очень сильно маловероятно, но пока не запрещено. Даже в числах до $10^{19}$. Вы снова приравниваете "практически равно" к "точно равно", а в математике это не так. И такое чётное число может вдруг найтись буквально следующим проверенным (если гипотеза неверна), сколь угодно малая околонулевая вероятность (что бы под ней не понимать) этого не запрещает.

[Ryzl]

Dmitriy40 в сообщении #1707157 писал(а):

Ryzl в сообщении #1707150 писал(а):

Вы предлагаете считать вхождение простых чисел не независимыми событиями? Т.е. вхождение каждого простого числа зависит от других?

Вообще говоря - да. Если число $p>3$ простое, то оба числа $p-1,p+1$ абсолютно точно составные и простыми быть никак не могут и значит вероятность для них вовсе не $1/\ln(x)$, а точно $0$.
Потому та оценка через обратных логарифм верна лишь в среднем, для очень больших чисел и интервалов, и чем больше, тем точнее.

Ryzl в сообщении #1707150 писал(а):

но это обоснование бессмысленности поиска таких четных чисел у которых не будет пар простых чисел дающих в сумме данное четное число. Экономия электроэнергии однако ))

И тоже нет. Даже если плюнуть на ошибки и скорректировать на много порядков, она хоть и останется чрезвычайно малой, но всё равно не нулевой и может случиться. Очень сильно маловероятно, но пока не запрещено. Даже в числах до $10^{19}$. Вы снова приравниваете "практически равно" к "точно равно", а в математике это не так. И такое чётное число может вдруг найтись буквально следующим проверенным (если гипотеза неверна), сколь угодно малая околонулевая вероятность (что бы под ней не понимать) этого не запрещает.

Ну то есть, вскипание чайника на металлической плите тоже может произойти вот вот, достаточно подождать?

[mihaild]

Ryzl
Давайте Вы всё-таки напишете, откуда у Вас случайность?

А я пока замечу, что Вы от "простых чисел" используете только асимптотическую плотность. Но я легко построю множество нечетных с той же асимптотической плотностью, такое что все четные числа представимы в виде двух чисел из этого множества, за исключением числа $10^{1000000} + 42$. Соответственно любое доказательство гипотезы Гольдбаха должно содержать пункт, который использует отличие моего множества от множества простых чисел.

[Dmitriy40]

(Оффтоп)

Ryzl в сообщении #1707158 писал(а):

Ну то есть, вскипание чайника на металлической плите тоже может произойти вот вот, достаточно подождать?

Математически - может.
Физически, впрочем, тоже может, запрета нет. Даже Солнце светит и греет потому что в нём ежесекундно реализуются события с весьма малой вероятностью. Побольше чем для чайника, но тоже очень далеко от 100%.
Вероятность дело такое, плохо понятное на бытовом уровне.

[Altenter]

Someone в сообщении #1706866 писал(а):

И очень напрягает термин "близнецы". Простые близнецы — это два простых числа, отличающихся на $2$ единицы. А "симметричными близнецами" в вашем смысле являются вообще все нечётные простые числа. Да и число $2$ симметрично самому себе относительно самого себя.

Ваши предложения для названия таких пар? Мне кажется, что название: простые близнецы с разностью $n$ вполне себя оправдывает и включает простых близнецов с разностью $2$ как частный случай. Слово симметричные- это свойство этих чисел, оно не требуется для их определения, а выводимо из него, поэтому в названии оно лишнее.

-- 28.10.2025, 17:32 --

Ryzl в сообщении #1706823 писал(а):

Вот распределение простых симметричных близнецов.



По моему интересно, нет?

Может быть как то приспособить для поиска претендентов? Точки (простые числа) визуально лежат на прямых.

Очень жирная белая линия на которой нет простых начинается, как мне кажется в районе числа $666= C_{37}^2$, где $37$ - первое простое иррегулярное число с номером $12$ в ряду простых. Неплохо было бы и еще проследить за такими линиями и посмотреть не связаны ли они с иррегулярными простыми.

[Skipper]

Ryzl в сообщении #1707150 писал(а):

Я и не говорю (хотя надеялся) что это доказательство гипотезы Гольдбаха, но это обоснование бессмысленности поиска таких четных чисел у которых не будет пар простых чисел дающих в сумме данное четное число

вероятность что случайно выбранное четное число (очень большое) опровергает гипотезу Гольдбаха -
(т.е. окажется таким что, нет суммы двух простых чисел, которые были бы равны этому числу) -
действительно стремится к нулю, (при увеличении рассматриваемых чисел).

Но тут нужно понимать, что и количество таких чисел-кандидатов бесконечно много!
Именно потому, (без строгого математического доказательства, что такая вероятность равна точно
нулю, а для этого надо знать глубоко аналитическую теорию чисел)
"на бесконечности" могут реализоваться сколь угодно малые вероятности..

Вот пример. Вероятность того что случайно выбранное число "в районе" гуголплекса,
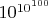
(то есть $10^{10^{100}} $ ) окажется простым- равна 1 разделить на логарифм
натуральный от гуголплекса, что равно порядка $ 2.3 \cdot 100^{100} $ ,
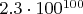
то есть больше чем гугол.

Предположим, у нас есть быстрый алгоритм определяющий простоту чисел гуголплекс + 1,
гуголплекс + 2, гуголплекс + 3, и т.д.. Пусть он проверяет их каждое за секунду.
Ясно что бессмысленно искать там перебором простые числа, и ждать, следующее встретится скорее всего
не ранее чем чайник вскипит на холодной плите. :)
И в чудовищное число раз дольше чем возраст Вселенной.
Ведь вероятность "попасть" на простое там, меньше чем 1 разделить на гугол.

Но однако же, доказано ещё Евклидом, что простых чисел бесконечно много.
А значит, и там рано или поздно встретится очередное простое число.

Поражает здесь то, что если верна одна из гипотез Харди-Литтлвуда, то там можно "дождаться",
что ВНЕЗАПНО встретятся не только "простые числа-близнецы", у которых разность $2$,
а даже сколь-угодно длинные "нетривиальные кортежи" простых чисел!
Например, кортеж длиной в $447 $ простых чисел на интервале $3159 $ ,
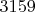
какого нет даже в самом начале числового ряда, с абсолютно максимальной плотностью
простых чисел ! (известно, что первые $446$ простых чисел лежат на интервале $3159 $ ).

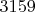
Вот такая "бесконечность", непостижимая для человеческого ума, штука..
Потому, пока строго математически не доказана гипотеза Гольдбаха, на бесконечности, вполне,
может встретиться четное число, опровергающее эту гипотезу. Хотя искать его на компьютере,
действительно смысла нет :)

Вот ещё пример.

Известно что возраст Вселенной $13,8$ миллиардов лет. Занумеруем годы, от т.н. "Большого Взрыва",
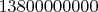
пусть ныне идёт $13800000000$ -й год.
Пусть во Вселенной происходит событие в каждом году, с вероятностью равной $1$ разделить на возраст Вселенной
в годах. Значит событие в нынешнем году, скорее всего не произойдёт! Ведь вероятность произойти,
всего лишь $1 / 13800000000$ .
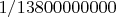
И так, чем дальше, тем всё эта вероятность уменьшается. В будущем, когда возраст Вселенной, будет
$100$ миллиардов лет, то вероятность произойти событию, будет уже $1$ разделить на $100$ миллиардов,
ну и так далее.
Пусть Вселенная в будущем существует бесконечное время. Вопрос- бесконечное ли количество
этих событий произойдёт в будущем?

Ответ удивителен- бесконечное!

А вот если вероятность события будет $1 / N ^ {(1 + \varepsilon)} $ ,
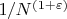
где $N $ - номер каждого года, с момента Большого Взрыва, $\varepsilon $ ,
это любое сколь угодно малое число, большее нуля, то..

Вероятности тоже убывают со временем, и число лет в будущем, тоже бесконечно..
Но в таком случае, число таких событий, которые произойдут, будет конечным!
То есть в любом случае, когда-то произойдёт последнее такое событие, и далее, несмотря,
на то, что ожидать будем бесконечное время, больше событий в такой модели не наступит.
Правда, об этом никогда нельзя будет узнать или доказать, ведь всегда вероятность будет ненулевая.

Вероятность стала слишком быстро убывать, так что уже и "бесконечное время ожидания" не помогает.

Вот это, одна из самых поразительных, завораживающих вещей, что я встречал в математике.
Где "бесконечности встречаются с конечным"..

[mihaild]

Skipper в сообщении #1707463 писал(а):

Поражает здесь то, что если верна одна из гипотез Харди-Литтлвуда, то там можно "дождаться", что ВНЕЗАПНО встретятся не только "простые числа-близнецы", у которых разность $2$, а даже сколь-угодно длинные "нетривиальные кортежи" простых чисел!

Кстати дождаться двух чисел, отличающихся не больше, чем на $246$, точно можно.

[Skipper]

mihaild в сообщении #1707466 писал(а):

Skipper в сообщении #1707463 писал(а):

Поражает здесь то, что если верна одна из гипотез Харди-Литтлвуда, то там можно "дождаться", что ВНЕЗАПНО встретятся не только "простые числа-близнецы", у которых разность $2$, а даже сколь-угодно длинные "нетривиальные кортежи" простых чисел!

Кстати дождаться двух чисел, отличающихся не больше, чем на $246$, точно можно.

Мда, это доказали. Один из самых замечательных прорывов в математике. Жаль, что остановились на $246$,
хотелось бы дождаться доказательства, что обычных простых чисел-близнецов с разностью $2$, бесконечно много..

[Someone]

Altenter в сообщении #1707446 писал(а):

Someone в сообщении #1706866 писал(а):

И очень напрягает термин "близнецы". Простые близнецы — это два простых числа, отличающихся на $2$ единицы. А "симметричными близнецами" в вашем смысле являются вообще все нечётные простые числа. Да и число $2$ симметрично самому себе относительно самого себя.

Ваши предложения для названия таких пар? Мне кажется, что название: простые близнецы с разностью $n$ вполне себя оправдывает и включает простых близнецов с разностью $2$ как частный случай. Слово симметричные- это свойство этих чисел, оно не требуется для их определения, а выводимо из него, поэтому в названии оно лишнее.

Видите ли, любая пара различных нечётных простых чисел — "симметричные близнецы" в смысле Ryzl. То есть, этот термин ничего не выделяет. Никакого свойства, кроме того, что это два различных нечётных простых числа. Зачем он нужен? Зачем предлагать какие-то названия, заведомо зная, что они ничего не означают и потому не нужны?

[Altenter]

Someone в сообщении #1707491 писал(а):

Altenter в сообщении #1707446 писал(а):

Someone в сообщении #1706866 писал(а):

И очень напрягает термин "близнецы". Простые близнецы — это два простых числа, отличающихся на $2$ единицы. А "симметричными близнецами" в вашем смысле являются вообще все нечётные простые числа. Да и число $2$ симметрично самому себе относительно самого себя.

Ваши предложения для названия таких пар? Мне кажется, что название: простые близнецы с разностью $n$ вполне себя оправдывает и включает простых близнецов с разностью $2$ как частный случай. Слово симметричные- это свойство этих чисел, оно не требуется для их определения, а выводимо из него, поэтому в названии оно лишнее.

Видите ли, любая пара различных нечётных простых чисел — "симметричные близнецы" в смысле Ryzl. То есть, этот термин ничего не выделяет. Никакого свойства, кроме того, что это два различных нечётных простых числа. Зачем он нужен? Зачем предлагать какие-то названия, заведомо зная, что они ничего не означают и потому не нужны?

Ну как же, доказано, что простых близнецов с разностью 246 существуен бесконечно много, а с разностью 2- неизвестно. В частности для того, чтобы не говорить в одном предложении: "Простых чисел с разностью 246 бесконечно много, а простых близнецов - неизвестно" - и вводятся простые близнецы с разностью n. И если мы их вводим, то: "Простых близнецов с разностью 246 бесконечно много, а с разностью 2- неизвестно"- звучит намного приятнее. А если не вводим, то тогда иногда должны избегать и употребление словосочетания "Простые близнецы" : "Простых чисел с разностью 246 бесконечно много, а с разностью 2- неизвестно". Но это все, конечно, вопросы договоренности, эстетики, удобства и субъективного восприятия.

[mihaild]

Altenter в сообщении #1707501 писал(а):

Ну как же, доказано, что простых близнецов с разностью 246 существуен бесконечно много

Это не доказано. А еще криво сформулировано: простые близнецы - это простые числа с разностью 2, простые близнецы с разностью 246 - это как квадрат $3 \times 4$.
Доказано, что для какого-то $n \leq 246$ существует бесконечно много пар простых, отличающихся ровно на $n$ (это тривиально эквивалентно тому, что есть бесконечно много пар простых, отличающихся не более чем на $246$). Легко может оказаться, что есть бесконечно много пар простых, отличающихся ровно на $42$, а вот для любого другого числа количество пар простых, отличающихся ровно на него, конечно.

[Altenter]

mihaild в сообщении #1707524 писал(а):

Altenter в сообщении #1707501 писал(а):

Ну как же, доказано, что простых близнецов с разностью 246 существуен бесконечно много

Это не доказано. А еще криво сформулировано: простые близнецы - это простые числа с разностью 2, простые близнецы с разностью 246 - это как квадрат $3 \times 4$.
Доказано, что для какого-то $n \leq 246$ существует бесконечно много пар простых, отличающихся ровно на $n$ (это тривиально эквивалентно тому, что есть бесконечно много пар простых, отличающихся не более чем на $246$). Легко может оказаться, что есть бесконечно много пар простых, отличающихся ровно на $42$, а вот для любого другого числа количество пар простых, отличающихся ровно на него, конечно.

Это сути не меняет в контексте терминологии. Эти пары надо называть либо простыми близнецами с разностью n, либо простые близнецы называть простыми числами с разностью 2 в целях единообразия выражений. Ну а так, конечно, это вопрос эстетики, удобства, привычки, субъективного восприятия, целесообразности и договоренности. Да, согласен, сформулировал мысль в математическом смысле криво, спасибо, что поправили.

[Someone]

Altenter в сообщении #1707501 писал(а):

простых близнецов с разностью 246

Нет никаких "простых близнецов с разностью $246$". Есть только простые близнецы с разностью $2$. По определению: простыми близнецами называются пары простых чисел с разностью $2$.
По сведениям сайта PrimePages, наибольшей известной парой простых близнецов является пара $2996863034895\cdot 2^{1290000}-1$ и $2996863034895\cdot 2^{1290000}+1$.
А, например, $7$ и $11$ — хоть и простые числа, но не близнецы, так как $11-7\neq 2$. Что Вам здесь ещё непонятно?
А "симметричные близнецы" в смысле Ryzl — это любая пара нечётных простых чисел. Например, $267$ и $26041$: их полусумма равна $13154$, и выполняется равенство $13154-267=26041-13154$. И, поскольку такое равенство можно написать для любой пары нечётных простых чисел, то все они являются "симметричными близнецами" в смысле Ryzl.

-- Ср окт 29, 2025 12:35:35 --

Altenter в сообщении #1707527 писал(а):

Это сути не меняет в контексте терминологии. Эти пары надо называть либо простыми близнецами с разностью n, либо простые близнецы называть простыми числами с разностью 2 в целях единообразия выражений.

Уж Вы извините математиков-недотёп, что они не посоветовались с Вами, кода формулировали определения.