https://ru.wikipedia.org/wiki/%D0%93%D0 ... 0%BA%D0%B0
Нет, это не то:
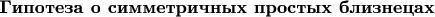
Пусть

— любое чётное число,
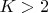
. Тогда:
1. Существует множество пар простых чисел

, таких что
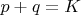
и
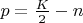
,
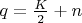
,
где

— натуральное число, причём количество таких пар может быть больше одной.
2. Для каждого простого числа

(для некоторого минимального порогового значения

)
существует хотя бы одно чётное число

, для которого
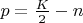
,
и
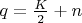
,
где

— простое число, т.е.

имеет симметричного простого близнеца

относительно середины
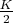
Эта гипотеза утверждает существование для каждого чётного числа пар простых чисел, симметричных относительно его половины, и для каждого простого числа в некотором диапазоне — существование соответствующего симметричного простого числа.
Существование пары простых чисел, симметричных относительно половины чётного числа (речь идёт, как я понимаю, исключительно о натуральных числах) — это гипотеза Гольдбаха в чуть-чуть другой формулировке. А "для каждого простого числа в некотором диапазоне — существование соответствующего симметричного простого числа" — непонятная формулировка. Какой диапазон имеется в виду? Чётное число

фиксировано или нет? Если фиксировано, то это неверно (например, если имеется в виду диапазон
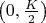
,
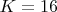
, а

, то "симметричное"

является составным), а если его можно выбирать произвольно, то тривиально: берём любые два нечётных простых числа

и

, их сумма
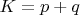
— чётное число, и его половина является "центром симметрии" чисел

и

. Впрочем, в начале темы почти всё это объяснялось. Но мне показалось, что Вы снова и снова возвращаетесь к этим идеям.
Тянет ли это на самостоятельную гипотезу?
Не тянет.
Тестировал до

кандидатов (сначала наличие для четных чисел симметричных пар близнецов простых чисел, затем для каждого простого числа наличие близнеца)
Тест до

прошел положительно.
А использовать это для поиска простых чисел можно? Брать большое четное и искать около его половины? (в тесте расхождение с серединой было не более 77)
Ну, Вам уже объясняли, что это то же самое, что искать где попало, поскольку каждое натуральное число является половиной целого.
Нужно иметь в виду, что если взять очень большое число, то может оказаться, что проверить его простоту за приемлемое время может оказаться невозможным: простоту случайно взятого числа, прошедшего некоторые предварительные тесты, скорее всего, придётся проверять одним из универсальных методов (например, методом эллиптических кривых;
о программе Primo я писал), которые требуют больших вычислительных ресурсов. Поэтому нужно искать простые числа специальных видов, для которых существуют специальные быстро работающие тесты (о программе PrimeForm GW я писал там же).
Собственно говоря, проверка гипотезы Гольдбаха для чётного числа

состоит в одновременном поиске двух положительных простых чисел в двух арифметических прогрессиях

и
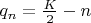
для одного и того же значения

. Здесь можно считать, что
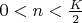
, так как замена

на

просто меняет местами числа

и

. Таким образом, здесь проверяется лишь конечное множество чисел. Поэтому есть положительная вероятность того, что во всех парах

,
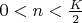
хотя бы одно из чисел будет составным. Поэтому доказательства гипотезы Гольдбаха вероятностным методом не получается.
Если же не требуется искать несколько "одновременно простых" чисел, то можно искать их в бесконечной арифметической прогрессии
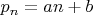
, где

и

— ненулевые взаимно простые целые числа (отрицательное целое число

считается простым, если
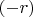
— простое число). Теорема Дирихле гарантирует, что в такой прогрессии содержится бесконечное множество простых чисел. Параметры

и

можно подобрать так, чтобы числа

имели "специальный" вид, допускающий сравнительно быструю проверку простоты.
Будем искать пары симметричных простых чисел в районе половины числа
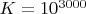
.