Видимо обсуждение можно заканчивать! )
Панамка у меня уже полная, начинает через край переваливаться....
Итоги:
1. Для любого четного числа существует множество пар симметричных относительно его половины нечетных чисел в сумме дающих это четное число.
2. Это множество состоит из четырех подмножеств: П-П, С-П, П-С, С-С. Где С- составное, П- простое
3. Вероятность того что подмножество П-П будет пустое стремиться у нулю.

4. Бессмысленно пытаться искать четное число у которого НЕ будет симметричной пары П-П (см. п 3.)
5. При возрастании N количество пар П-П возрастает (см. график выше)

Если считать распределение пар как пуассоновское, вероятность отсутствия хоть одной пары П-П для
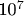
будет:
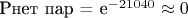
т.е. практически нулевая, и с ростом N эта вероятность будет только уменьшаться.
P.S. Для числа 16 существует две пары простых симметричных близнецов [5,11] и [3,13], я нигде не утверждал что КАЖДОЕ простое число имеет своего симметричного простого близнеца.